Hai đường thẳng song song Kết nối tri thức
Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Hai đường thẳng song song bao gồm vị trí tương đối của hai đường thẳng và tính chất hai đường thẳng song song trong không gian. Ngoài ra có các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.
1. Vị trí tương đối của hai đường thẳng
Cho hai đường thẳng 
\(a\) và \(b\) trong không gian.
Nếu \(a\) và \(b\) cùng nằm trong một mặt phẳng thì ta nói \(a\) và \(b\) đồng phẳng. Khi đó \(a\) và \(b\) có thể cắt nhau, song song với nhau hoặc trùng nhau.
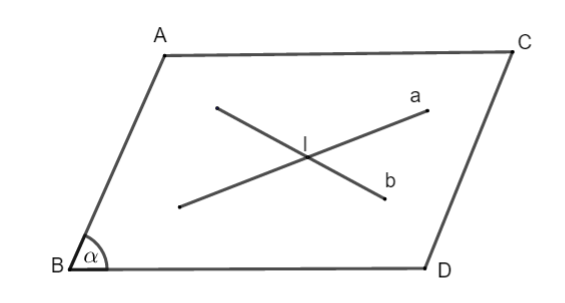
Trường hợp 1: \(a, b\) đồng phẳng
Đường thẳng \(a\) cắt đường thẳng \(b\) tại một điểm, \(a \cap b = \left\{ I \right\}\)
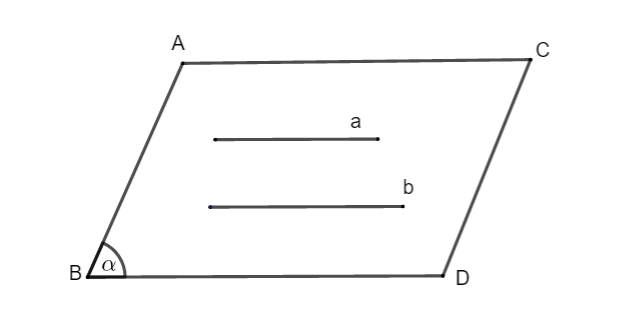
+ Đường thẳng \(a\) song song với đường thẳng \(b\), \(a // b\)
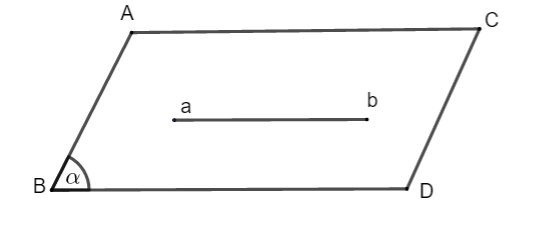
+ Đường thẳng \(a\) trùng với đường thẳng \(b\), \(a \equiv b\)
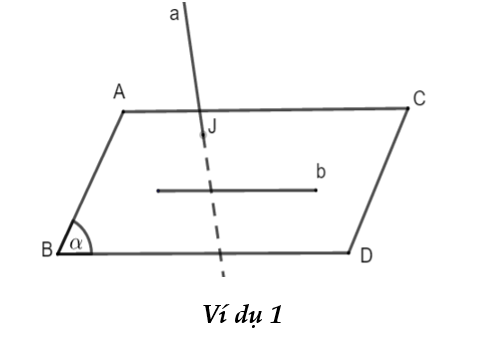
Nếu \(a\) và b không cùng nằm trong bất kì mặt phẳng nào thì ta nói \(a\) và \(b\) chéo nhau. Khi đó ta cũng nói \(a\) chéo với \(b\) hoặc \(b\) chéo với \(a\).
Trường hợp 2: \(a, b\) không đồng phẳng
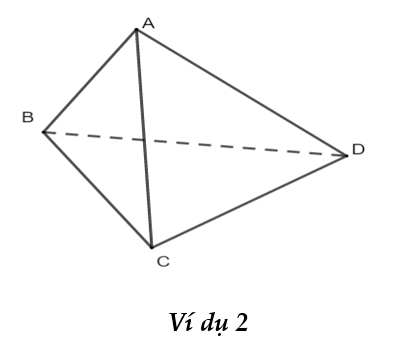
Theo hình vẽ ở trên ta nói \(a\) chéo với \(b\) hoặc \(b\) chéo với \(a\).
Ở ví dụ 2 các cặp cạnh chéo nhau là: AC và BD, AB và CD, …
Nhận xét:
+ Hai đường thẳng không có điểm chung thì có thể song song hoặc chéo nhau.
+ Hai đường thẳng song song là hai đường thẳng đồng phẳng và không có điểm chung.
+ Có đúng một mặt phẳng chứa hai đường thẳng song song.
2. Tính chất của hai đường thẳng song song
- Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.
- Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.
- Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đôi một song song với nhau.
Chú ý: Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Ví dụ: Cho hình chóp \(S.ABCD\) có đáy là tứ giác lồi. Gọi \(M, N\) lần lượt là trọng tâm tam giác \(SAB\) và \(SAD\). Lấy \(E\) là trung điểm của \(BC\).
a) Chứng minh \(MN // BD\).
b) Gọi \(U, T\) là giao điểm của \((MNE)\) với \(SD\) và \(SB\). Chứng minh \(UT // BD\).
Hướng dẫn giải
Hình vẽ minh họa
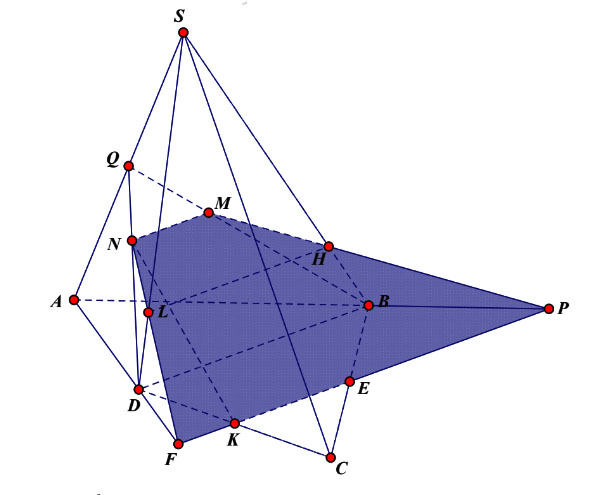
Gọi Q là trung điểm của SA
Xét tam giác QBD có
\(\frac{{QN}}{{DQ}} = \frac{{QM}}{{QB}} = \frac{1}{3}\) (Theo tính chất trọng tâm tam giác)
Vậy \(MN//BD\)
b) Dựng \(EK//MN \Rightarrow \left( {MNE} \right) \equiv \left( {MNKE} \right)\)
Tìm \(L = \left( {MNE} \right) \cap SB;SB \subset \left( {SAD} \right)\); gọi \(F = AD \cap KE\)
\(\Rightarrow H = MP \cap SB\)
Ta có: \(\left\{ \begin{gathered}
MN \subset \left( {MNE} \right) \hfill \\
BD \subset \left( {SBD} \right) \hfill \\
MN//BD \hfill \\
\left( {MNE} \right) \cap \left( {SBD} \right) = LH \hfill \\
\end{gathered} \right.\)
\(\Rightarrow LH//BD//MN\)
