Phương trình, bất phương trình mũ và Lôgarit Kết nối tri thức
Bộ tài liệu Lí thuyết Toán 11 Kết nối tri thức: Phương trình, bất phương trình mũ và lôgarit bao gồm định nghĩa, tính chất và cách giải phương trình, bất phương trình mũ và lôgarit. Ngoài ra có các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 11 KNTT giúp các em dễ dàng ôn tập củng cố.
1. Phương trình mũ
a) Định nghĩa phương trình mũ
Phương trình mũ cơ bản có dạng
![]() \({a^x} = b{\text{ }}\left( {a > 0,{\text{ }}a \ne 1} \right)\)
\({a^x} = b{\text{ }}\left( {a > 0,{\text{ }}a \ne 1} \right)\)
Để giải phương trình mũ, ta xét hai trường hợp sau:
- Phương trình có một nghiệm duy nhất khi
 \(b > 0\)
\(b > 0\) - Phương trình vô nghiệm khi
 \(b \leq 0\)
\(b \leq 0\)
Ta minh họa bằng đồ thị sau:
- Với
 \(a>1\), ta có đồ thị sau
\(a>1\), ta có đồ thị sau
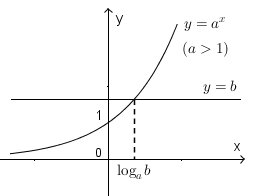
- Với
 \(0 < a < 1\), ta có đồ thị sau.
\(0 < a < 1\), ta có đồ thị sau.
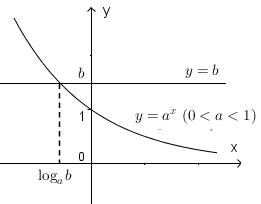
b) Cách giải phương trình mũ
i) Biến đổi, quy về cùng cơ số
![]() \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow a = 1\) hoặc
\({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow a = 1\) hoặc ![]() \(\left\{ \begin{gathered}
0 < a \ne 1 \hfill \\
f\left( x \right) = g\left( x \right) \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered}
0 < a \ne 1 \hfill \\
f\left( x \right) = g\left( x \right) \hfill \\
\end{gathered} \right.\)
Ví dụ: Cho phương trình: ![]() \({3^{{x^2} - 3x + 8}} = {9^{2{\text{x}} - 1}}\). Tìm tập nghiệm của phương trình ?
\({3^{{x^2} - 3x + 8}} = {9^{2{\text{x}} - 1}}\). Tìm tập nghiệm của phương trình ?
Hướng dẫn giải
Ta có: ![]() \({3^{{x^2} - 3x + 8}} = {9^{2{\text{x}} - 1}}\)
\({3^{{x^2} - 3x + 8}} = {9^{2{\text{x}} - 1}}\)
![]() \(\Leftrightarrow {3^{{x^2} - 3x + 8}} = {3^{4{\text{x}} - 2}} \Leftrightarrow {x^2} - 3x + 8 = 4{\text{x}} - 2\)
\(\Leftrightarrow {3^{{x^2} - 3x + 8}} = {3^{4{\text{x}} - 2}} \Leftrightarrow {x^2} - 3x + 8 = 4{\text{x}} - 2\)
![]() \(\Leftrightarrow {x^2} - 7x + 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 5} \\
{x = 2}
\end{array}} \right.\)
\(\Leftrightarrow {x^2} - 7x + 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 5} \\
{x = 2}
\end{array}} \right.\)
Vậy phương trình có tập nghiệm là ![]() \(S = \left\{ {2;5} \right\}\)
\(S = \left\{ {2;5} \right\}\)
ii) Đặt ẩn phụ
![f\left[ {{a^{g\left( x \right)}}} \right] = 0 \,\ { }{\text{ }}\left( {0 < a \ne 1} \right){\text{ }} \Leftrightarrow {\text{ }}\left\{ \begin{gathered}
t = {a^{g\left( x \right)}} > 0 \hfill \\
f\left( t \right) = 0 \hfill \\
\end{gathered} \right.](https://st.vndoc.com/data/image/blank.png) \(f\left[ {{a^{g\left( x \right)}}} \right] = 0 \,\ { }{\text{ }}\left( {0 < a \ne 1} \right){\text{ }} \Leftrightarrow {\text{ }}\left\{ \begin{gathered}
t = {a^{g\left( x \right)}} > 0 \hfill \\
f\left( t \right) = 0 \hfill \\
\end{gathered} \right.\)
\(f\left[ {{a^{g\left( x \right)}}} \right] = 0 \,\ { }{\text{ }}\left( {0 < a \ne 1} \right){\text{ }} \Leftrightarrow {\text{ }}\left\{ \begin{gathered}
t = {a^{g\left( x \right)}} > 0 \hfill \\
f\left( t \right) = 0 \hfill \\
\end{gathered} \right.\)
Ta thường gặp các dạng:
 \(m.{a^{2f\left( x \right)}} + n.{a^{f\left( x \right)}} + p = 0\)
\(m.{a^{2f\left( x \right)}} + n.{a^{f\left( x \right)}} + p = 0\) \(m.{a^{f\left( x \right)}} + n.{b^{f\left( x \right)}} + p = 0\), trong đó
\(m.{a^{f\left( x \right)}} + n.{b^{f\left( x \right)}} + p = 0\), trong đó  \(a.b=1\). Đặt
\(a.b=1\). Đặt  \(t = {a^{f\left( x \right)}},{\text{ }}t > 0\), suy ra
\(t = {a^{f\left( x \right)}},{\text{ }}t > 0\), suy ra  \({b^{f\left( x \right)}} = \frac{1}{t}\).
\({b^{f\left( x \right)}} = \frac{1}{t}\). \(m.{a^{2f\left( x \right)}} + n.{\left( {a.b} \right)^{f\left( x \right)}} + p.{b^{2f\left( x \right)}} = 0\). Chia hai vế cho
\(m.{a^{2f\left( x \right)}} + n.{\left( {a.b} \right)^{f\left( x \right)}} + p.{b^{2f\left( x \right)}} = 0\). Chia hai vế cho  \({b^{2f\left( x \right)}}\) và đặt
\({b^{2f\left( x \right)}}\) và đặt  \({\left( {\frac{a}{b}} \right)^{f\left( x \right)}} = t > 0\).
\({\left( {\frac{a}{b}} \right)^{f\left( x \right)}} = t > 0\).
Ví dụ: Phương trình ![]() \({3^{1 - x}} = 2 + {\left( {\frac{1}{9}} \right)^x}\) có bao nhiêu nghiệm âm?
\({3^{1 - x}} = 2 + {\left( {\frac{1}{9}} \right)^x}\) có bao nhiêu nghiệm âm?
Hướng dẫn giải
Phương trình tương đương với ![]() \(\frac{3}{{{3^x}}} = 2 + {\left( {\frac{1}{9}} \right)^x}\)
\(\frac{3}{{{3^x}}} = 2 + {\left( {\frac{1}{9}} \right)^x}\)![]() \(\Leftrightarrow 3.{\left( {\frac{1}{3}} \right)^x} = 2 + {\left( {\frac{1}{3}} \right)^{2x}}\).
\(\Leftrightarrow 3.{\left( {\frac{1}{3}} \right)^x} = 2 + {\left( {\frac{1}{3}} \right)^{2x}}\).
Đặt ![]() \(t = {\left( {\frac{1}{3}} \right)^x}\),
\(t = {\left( {\frac{1}{3}} \right)^x}\), ![]() \(t > 0\).
\(t > 0\).
Phương trình trở thành ![]() \(3t = 2 + {t^2} \Leftrightarrow {t^2} - 3t + 2 = 0 \Leftrightarrow \left[ \begin{gathered}
t = 1 \hfill \\
t = 2 \hfill \\
\end{gathered} \right.\).
\(3t = 2 + {t^2} \Leftrightarrow {t^2} - 3t + 2 = 0 \Leftrightarrow \left[ \begin{gathered}
t = 1 \hfill \\
t = 2 \hfill \\
\end{gathered} \right.\).
- Với
 \(t=1\), ta được
\(t=1\), ta được  \({\left( {\frac{1}{3}} \right)^x} = 1 \Leftrightarrow x = 0\).
\({\left( {\frac{1}{3}} \right)^x} = 1 \Leftrightarrow x = 0\). - Với
 \(t=2\), ta được
\(t=2\), ta được  \({\left( {\frac{1}{3}} \right)^x} = 2 \Leftrightarrow x = {\log _{\frac{1}{3}}}2 = - {\log _3}2 < 0\).
\({\left( {\frac{1}{3}} \right)^x} = 2 \Leftrightarrow x = {\log _{\frac{1}{3}}}2 = - {\log _3}2 < 0\).
Vậy phương trình có một nghiệm âm.
iii) Logarit hóa
Phương trình ![]() \({a^{f\left( x \right)}} = b \Leftrightarrow \left\{ \begin{gathered}
0 < a \ne 1,{\text{ }}b > 0 \hfill \\
f\left( x \right) = {\log _a}b \hfill \\
\end{gathered} \right.\).
\({a^{f\left( x \right)}} = b \Leftrightarrow \left\{ \begin{gathered}
0 < a \ne 1,{\text{ }}b > 0 \hfill \\
f\left( x \right) = {\log _a}b \hfill \\
\end{gathered} \right.\).
Phương trình ![]() \({a^{f\left( x \right)}} = {b^{g\left( x \right)}} \Leftrightarrow {\log _a}{a^{f\left( x \right)}} = {\log _a}{b^{g\left( x \right)}}\)
\({a^{f\left( x \right)}} = {b^{g\left( x \right)}} \Leftrightarrow {\log _a}{a^{f\left( x \right)}} = {\log _a}{b^{g\left( x \right)}}\)![]() \(\Leftrightarrow f\left( x \right) = g\left( x \right).{\log _a}b\)
\(\Leftrightarrow f\left( x \right) = g\left( x \right).{\log _a}b\)
hoặc ![]() \({\log _b}{a^{f\left( x \right)}} = {\log _b}{b^{g\left( x \right)}} \Leftrightarrow f\left( x \right).{\log _b}a = g\left( x \right).\)
\({\log _b}{a^{f\left( x \right)}} = {\log _b}{b^{g\left( x \right)}} \Leftrightarrow f\left( x \right).{\log _b}a = g\left( x \right).\)
Ví dụ: Ta có nghiệm của phương trình ![]() \(3^x=2\) là
\(3^x=2\) là ![]() \(x = {\log _3}2\)
\(x = {\log _3}2\)
2. Phương trình Lôgarit
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
Phương trình lôgarit cơ bản có dạng:
![]() \({\log _a}f(x) = b\)
\({\log _a}f(x) = b\) ![]() \((a > 0,\,\,a \ne 1 )\)
\((a > 0,\,\,a \ne 1 )\)
Để giải phương trình lôgarit cơ bản, ta có:
![]() \({\log _a}f(x) = b \Leftrightarrow x =a^b\)
\({\log _a}f(x) = b \Leftrightarrow x =a^b\)
Ta minh họa bằng đồ thị như sau
- Với
 \(a>1\), ta có đồ thị sau:
\(a>1\), ta có đồ thị sau:
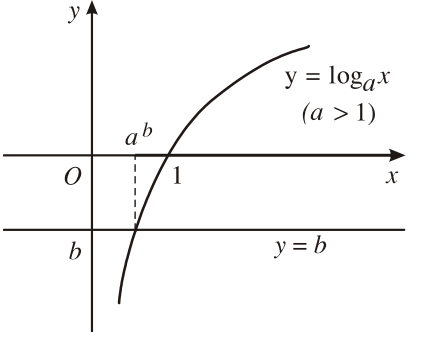
- Với
 \(0 < a < 1\), ta có đồ thị sau:
\(0 < a < 1\), ta có đồ thị sau:
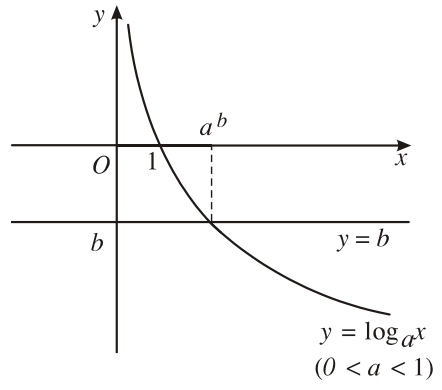
Quan sát đồ thị, ta thấy rằng:
- Trường hợp :
 \(a>1\):
\(a>1\):  \({\log _a}x > b\) khi và chỉ khi
\({\log _a}x > b\) khi và chỉ khi  \(x > {a^b}\)
\(x > {a^b}\) - Trường hợp :
 \(0 < a < 1\):
\(0 < a < 1\):  \({\log _a}x > b\) khi và chỉ khi
\({\log _a}x > b\) khi và chỉ khi  \(0 < x < {a^b}\).
\(0 < x < {a^b}\).
b) Cách giải phương trình lôgarit
i) Biến đổi, quy về cùng cơ số
![]() \({\log _a}f(x) = {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) = g(x) \hfill \\
\end{gathered} \right.\) , với mọi
\({\log _a}f(x) = {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) = g(x) \hfill \\
\end{gathered} \right.\) , với mọi ![]() \(0 < a \ne 1\)
\(0 < a \ne 1\)
Ví dụ: Phương trình ![]() \({\log _2}(3x - 2) = 2\) có nghiệm là?
\({\log _2}(3x - 2) = 2\) có nghiệm là?
Hướng dẫn giải
![]() \({\log _2}(3x - 2) = 2\)
\({\log _2}(3x - 2) = 2\)
 \(\Leftrightarrow \left\{ \begin{gathered}
3x - 2 > 0 \hfill \\
3x - 2 = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x > \frac{3}{2} \hfill \\
x = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow x = 2\)
\(\Leftrightarrow \left\{ \begin{gathered}
3x - 2 > 0 \hfill \\
3x - 2 = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x > \frac{3}{2} \hfill \\
x = 2 \hfill \\
\end{gathered} \right. \Leftrightarrow x = 2\)
Vậy phương trình có nghiệm là ![]() \(x=2\)
\(x=2\)
ii) Đặt ẩn phụ
Ví dụ: Tìm nghiệm của phương trình sau: ![]() \(\frac{1}{{4 - \lg x}} + \frac{2}{{2 + \lg x}} = 1\)
\(\frac{1}{{4 - \lg x}} + \frac{2}{{2 + \lg x}} = 1\)
Hướng dẫn giải
Đặt ![]() \(t = \lg x\)
\(t = \lg x\)
PT ![]() \(\Leftrightarrow \frac{1}{{4 - t}} + \frac{2}{{2 + t}} = 1 \Leftrightarrow \frac{{2 + t + 2(4 - t)}}{{(4 - t)(2 + t)}} = 1\)
\(\Leftrightarrow \frac{1}{{4 - t}} + \frac{2}{{2 + t}} = 1 \Leftrightarrow \frac{{2 + t + 2(4 - t)}}{{(4 - t)(2 + t)}} = 1\)
![]() \(\Leftrightarrow 2 + t + 2(4 - t) = (4 - t)(2 + t)\)
\(\Leftrightarrow 2 + t + 2(4 - t) = (4 - t)(2 + t)\)
![]() \(\Leftrightarrow 10 - t = 8 + 2t - {t^2} \Leftrightarrow {t^2} - 3t + 2 = 0\)
\(\Leftrightarrow 10 - t = 8 + 2t - {t^2} \Leftrightarrow {t^2} - 3t + 2 = 0\)
Nhẩm nghiệm có hệ số ![]() \(a+b+c=1-3+2=0\) nên phương trình ẩn
\(a+b+c=1-3+2=0\) nên phương trình ẩn ![]() \(t\) có 2 nghiệm là 1 và 2.
\(t\) có 2 nghiệm là 1 và 2.
Suy ra ![]() \(1 = \lg x\) hoặc
\(1 = \lg x\) hoặc ![]() \(2 = \lg x\).
\(2 = \lg x\).
Do đó phương trình đã cho có nghiệm là ![]() \(x=e\) hoặc
\(x=e\) hoặc ![]() \(x = e^2\).
\(x = e^2\).
Vậy phương trình có tập nghiệm là ![]() \(x = \{ e; e^2 \}\)
\(x = \{ e; e^2 \}\)
iii) Mũ hóa
Ví dụ: Phương trình ![]() \({\log _2}\left( {{{3.2}^x} - 1} \right) = 2x + 1\) có bao nhiêu nghiệm?
\({\log _2}\left( {{{3.2}^x} - 1} \right) = 2x + 1\) có bao nhiêu nghiệm?
Hướng dẫn giải
Ta có: ![]() \({\log _2}\left( {{{3.2}^x} - 1} \right) = 2x + 1 \Leftrightarrow {3.2^x} - 1 = {2^{2x + 1}}\)
\({\log _2}\left( {{{3.2}^x} - 1} \right) = 2x + 1 \Leftrightarrow {3.2^x} - 1 = {2^{2x + 1}}\)
 \(\Leftrightarrow {2.4^x} - {3.2^x} + 1 = 0 \Leftrightarrow \left[ \begin{gathered}
{2^x} = 1 \hfill \\
{2^x} = \frac{1}{2} \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = - 1 \hfill \\
\end{gathered} \right.\)
\(\Leftrightarrow {2.4^x} - {3.2^x} + 1 = 0 \Leftrightarrow \left[ \begin{gathered}
{2^x} = 1 \hfill \\
{2^x} = \frac{1}{2} \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = - 1 \hfill \\
\end{gathered} \right.\)
Vậy phương trình đã cho có tất cả 2 nghiệm.
3. Bất phương trình mũ
a) Định nghĩa bất phương trình mũ
Bất phương trình mũ cơ bản có dạng ![]() \({a^x} > b\) (hoặc
\({a^x} > b\) (hoặc ![]() \({a^x} \geqslant b,{a^x} < b,{a^x} \leqslant b\)) với
\({a^x} \geqslant b,{a^x} < b,{a^x} \leqslant b\)) với ![]() \(a > 0,a \ne 1\).
\(a > 0,a \ne 1\).
Để giải, ta xét bất phương trình có dạng ![]() \({a^x} > b\)
\({a^x} > b\)
- Nếu ![]() \(b \leq 0\), tập nghiệm của bất phương trình là
\(b \leq 0\), tập nghiệm của bất phương trình là ![]() \(\mathbb{R}\), vì
\(\mathbb{R}\), vì ![]() \({a^x} > b,\forall x \in \mathbb{R}\)
\({a^x} > b,\forall x \in \mathbb{R}\)
- Nếu ![]() \(b > 0\) thì bất phương trình tương đương với
\(b > 0\) thì bất phương trình tương đương với ![]() \({a^x} > {a^{{{\log }_a}b}}\), khi đó:
\({a^x} > {a^{{{\log }_a}b}}\), khi đó:
Với ![]() \(a>1\), nghiệm của bất phương trình là
\(a>1\), nghiệm của bất phương trình là ![]() \(x > {\log _a}b\)
\(x > {\log _a}b\)
Với ![]() \(0 < a < 1\), nghiệm của bất phương trình là
\(0 < a < 1\), nghiệm của bất phương trình là ![]() \(x < {\log _a}b\)
\(x < {\log _a}b\)
b) Cách giải bất phương trình mũ
- Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
 \(\boxed{{a^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
a > 1 \hfill \\
f\left( x \right) > g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
0 < a < 1 \hfill \\
f\left( x \right) < g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.}\)
\(\boxed{{a^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
a > 1 \hfill \\
f\left( x \right) > g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
0 < a < 1 \hfill \\
f\left( x \right) < g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.}\)
- Tương tự với bất phương trình dạng:
 \(\left[ \begin{gathered}
{a^{f\left( x \right)}} \geqslant {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} < {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} \leqslant {a^{g\left( x \right)}} \hfill \\
\end{gathered} \right.\)
\(\left[ \begin{gathered}
{a^{f\left( x \right)}} \geqslant {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} < {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} \leqslant {a^{g\left( x \right)}} \hfill \\
\end{gathered} \right.\)
- Trong trường hợp cơ số
 \(a\) có chứa ẩn số thì:
\(a\) có chứa ẩn số thì:
![]() \(\boxed{{a^M} > {a^N} \Leftrightarrow \left( {a - 1} \right)\left( {M - N} \right) > 0}\).
\(\boxed{{a^M} > {a^N} \Leftrightarrow \left( {a - 1} \right)\left( {M - N} \right) > 0}\).
- Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ: đưa về cùng cơ số; đặt ẩn phụ.
Ví dụ: Tập nghiệm của bất phương trình ![]() \({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)là?
\({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)là?
Hướng dẫn giải
Ta có: ![]() \({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)
\({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)
![]() \(\Leftrightarrow {3.2^x} \leqslant \frac{4}{3}{.3^x}\)
\(\Leftrightarrow {3.2^x} \leqslant \frac{4}{3}{.3^x}\)![]() \(\Leftrightarrow {\left( {\frac{3}{2}} \right)^x} \geqslant \frac{9}{4}\)
\(\Leftrightarrow {\left( {\frac{3}{2}} \right)^x} \geqslant \frac{9}{4}\)
![]() \(\Leftrightarrow x \geqslant 2\)
\(\Leftrightarrow x \geqslant 2\)
Vậy bất phương trình có tập nghiệm là ![]() \(x \in \left[ {2; + \infty } \right)\).
\(x \in \left[ {2; + \infty } \right)\).
4. Bất phương trình Lôgarit
a) Định nghĩa bất phương trình lôgarit
Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
Bất phương trình logarit cơ bản có dạng ![]() \({\log _a}x > b\) (hoặc
\({\log _a}x > b\) (hoặc ![]() \({\log _a}x \geqslant b,\)
\({\log _a}x \geqslant b,\)![]() \({\log _a}x < b,\)
\({\log _a}x < b,\)![]() \({\log _a}x \leqslant b\)) với
\({\log _a}x \leqslant b\)) với ![]() \(a > 0,a \ne 1\).
\(a > 0,a \ne 1\).
Để giải, ta xét bất phương trình ![]() \({\log _a}x > b\) như sau:
\({\log _a}x > b\) như sau:
- Trường hợp ![]() \(a>1\), ta có:
\(a>1\), ta có:
![]() \({\log _a}x > b \Leftrightarrow x > {a^b}\)
\({\log _a}x > b \Leftrightarrow x > {a^b}\)
- Trường hợp ![]() \(0 < a < 1\), ta có:
\(0 < a < 1\), ta có:
![]() \({\log _a}x > b \Leftrightarrow 0 < x < {a^b}\)
\({\log _a}x > b \Leftrightarrow 0 < x < {a^b}\)
b) Cách giải bất phương trình lôgarit
i) Đưa về cùng cơ số
Nếu ![]() \(a> 1\) thì
\(a> 1\) thì
![]() \({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
g(x) > 0 \hfill \\
f(x) > g(x) \hfill \\
\end{gathered} \right.\)
\({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
g(x) > 0 \hfill \\
f(x) > g(x) \hfill \\
\end{gathered} \right.\)
Nếu ![]() \(0 < a < 1\) thì
\(0 < a < 1\) thì
![]() \({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) < g(x) \hfill \\
\end{gathered} \right.\)
\({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) < g(x) \hfill \\
\end{gathered} \right.\)
ii) Đặt ẩn phụ
iii) Mũ hóa
Ví dụ: Tìm tập nghiệm của Bất phương trình ![]() \({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\)
\({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\)
Giải:
+) Xét: ![]() \(x > 0 \Rightarrow {2^x} > {2^0} = 1 \Rightarrow {2^x} + 1 > 2\)
\(x > 0 \Rightarrow {2^x} > {2^0} = 1 \Rightarrow {2^x} + 1 > 2\) ![]() \(\Rightarrow {\log _2}\left( {{2^x} + 1} \right) > {\log _2}2 = 1\left( 1 \right)\)
\(\Rightarrow {\log _2}\left( {{2^x} + 1} \right) > {\log _2}2 = 1\left( 1 \right)\)
![]() \(x > 0 \Rightarrow {4^x} > {4^0} = 1 \Rightarrow {4^x} + 2 > 2 + 1 = 3\)
\(x > 0 \Rightarrow {4^x} > {4^0} = 1 \Rightarrow {4^x} + 2 > 2 + 1 = 3\) ![]() \(\Rightarrow {\log _3}\left( {{4^x} + 2} \right) > {\log _3}3 = 1\left( 2 \right)\)
\(\Rightarrow {\log _3}\left( {{4^x} + 2} \right) > {\log _3}3 = 1\left( 2 \right)\)
Cộng vế với vế của (1) và (2) ta được:
![]() \({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) > 2\)
\({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) > 2\)
Mà bất phương trình:
![]() \({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\) nên
\({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\) nên ![]() \(x > 0 (L)\)
\(x > 0 (L)\)
+) Xét: ![]() \(x \leqslant 0 \Rightarrow {2^x} \leqslant {2^0} = 1 \Rightarrow {2^x} + 1 \leqslant 2\)
\(x \leqslant 0 \Rightarrow {2^x} \leqslant {2^0} = 1 \Rightarrow {2^x} + 1 \leqslant 2\) ![]() \(\Rightarrow {\log _2}\left( {{2^x} + 1} \right) \leqslant {\log _2}2 = 1\left( 3 \right)\)
\(\Rightarrow {\log _2}\left( {{2^x} + 1} \right) \leqslant {\log _2}2 = 1\left( 3 \right)\)
![]() \(x \leqslant 0 \Rightarrow {4^x} \leqslant {4^0} = 1 \Rightarrow {4^x} + 2 \leqslant 2 + 1 = 3\)
\(x \leqslant 0 \Rightarrow {4^x} \leqslant {4^0} = 1 \Rightarrow {4^x} + 2 \leqslant 2 + 1 = 3\) ![]() \(\Rightarrow {\log _3}\left( {{4^x} + 2} \right) \leqslant {\log _3}3 = 1\left( 4 \right)\)
\(\Rightarrow {\log _3}\left( {{4^x} + 2} \right) \leqslant {\log _3}3 = 1\left( 4 \right)\)
Cộng vế với vế của (3) và (4) ta được:
![]() \({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\left( {TM} \right)\)
\({\log _2}({2^x} + 1) + {\log _3}({4^x} + 2) \leqslant 2\left( {TM} \right)\)
Vậy ![]() \(x \leqslant 0\) hay
\(x \leqslant 0\) hay ![]() \(x \in \left( { - \infty ;0} \right]\).
\(x \in \left( { - \infty ;0} \right]\).






