Tính giá trị lượng giác
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính
. Tính ![]()
Ta có:
Đề kiểm tra 15 phút Toán 10 Chương 3 Hệ thức lượng trong tam giác sách Kết nối tri thức giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Tính giá trị lượng giác
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Tính
. Tính ![]()
Ta có:
Tính bán kính đường tròn ngoại tiếp tam giác
Tam giác ![]() vuông tại
vuông tại ![]() có đường cao
có đường cao ![]() và
và ![]() . Tính bán kính
. Tính bán kính ![]() của đường tròn ngoại tiếp tam giác
của đường tròn ngoại tiếp tam giác ![]() .
.
Tam giác vuông tại
có đường cao
Mặt khác thế vào
ta được
Suy ra
Vậy bán kính cần tìm là
Tính số đo góc C
Cho tam giác ![]() thỏa mãn
thỏa mãn ![]() . Khi đó, góc
. Khi đó, góc ![]() có số đo là:
có số đo là:
Theo đề bài ra ta có:
.
Tính diện tích tam giác
Cho ![]() có
có ![]() Diện tích
Diện tích ![]() của tam giác trên là:
của tam giác trên là:
Ta có: Nửa chu vi :
.
Áp dụng công thức Hê-rông:
.
Chọn mệnh đề đúng
Gọi ![]() là tổng bình phương độ dài ba trung tuyến của tam giác
là tổng bình phương độ dài ba trung tuyến của tam giác ![]() . Trong các mệnh đề sau mệnh đề nào đúng?
. Trong các mệnh đề sau mệnh đề nào đúng?
Ta có:
Tính diện tích tam giác
Cho ![]() có
có ![]() Diện tích của tam giác là:
Diện tích của tam giác là:
Ta có:
Tính khoảng cách hai tàu sau 2 giờ
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí ![]() , đi thẳng theo hai hướng tạo với nhau một góc
, đi thẳng theo hai hướng tạo với nhau một góc ![]() . Tàu thứ nhất chạy với tốc độ
. Tàu thứ nhất chạy với tốc độ ![]() , tàu thứ hai chạy với tốc độ
, tàu thứ hai chạy với tốc độ ![]() . Hỏi sau
. Hỏi sau ![]() giờ hai tàu cách nhau bao nhiêu
giờ hai tàu cách nhau bao nhiêu ![]() ?
?
Sau quãng đường tàu thứ nhất chạy được là:
Sau quãng đường tàu thứ hai chạy được là:
Vậy sau hai tàu cách nhau là:
Tìm câu sai
Cho ![]() và
và ![]() là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
Mối liên hệ hai cung bù nhau.
Tính số đo góc A
Cho tam giác ![]() thỏa mãn:
thỏa mãn: ![]() . Khi đó:
. Khi đó:
Ta có:
Chọn phương án đúng
Giá trị của ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có: .
Chọn đẳng thức đúng
Trong các đẳng thức sau, đẳng thức nào đúng?
Đáp án đúng là sin(180° – α) = sin α
Tính giá trị của biểu thức
Giá trị của ![]() là
là
Ta có:
.
Tính độ dài cạnh b
Cho tam giác ![]() có
có ![]() . Hỏi độ dài cạnh b bằng bao nhiêu?
. Hỏi độ dài cạnh b bằng bao nhiêu?
Áp dụng định lí sin:
.
Tính khoảng cách AB
Khoảng cách từ ![]() đến
đến ![]() không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm
không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm ![]() mà từ đó có thể nhìn được
mà từ đó có thể nhìn được ![]() và
và ![]() dưới một góc
dưới một góc ![]() . Biết
. Biết ![]() . Khoảng cách
. Khoảng cách ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
Xác định dấu của biểu thức
Cho ![]() . Xác định dấu của biểu thức
. Xác định dấu của biểu thức ![]()
Ta có:
và
Tính độ dài cạnh BC
Trong tam giác ABC có ![]() và
và ![]() . Tính độ dài cạnh BC.
. Tính độ dài cạnh BC.
Áp dụng định lí cosin cho tam giác ABC ta có:
Tính giá trị của biểu thức P
Cho góc ![]() thỏa mãn
thỏa mãn ![]() Tính
Tính ![]()
Từ giả thiết, ta có
.
Tính độ dài cạnh còn lại của tam giác
Tam giác ![]() có
có ![]() Độ dài cạnh
Độ dài cạnh ![]() bằng bao nhiêu?
bằng bao nhiêu?
Ta có:
.
Tính giá trị lượng giác
Cho góc ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() Tính
Tính ![]()
Ta có
Tìm khẳng định sai
Cho hai góc nhọn ![]() và
và ![]() , (
, (![]() . Khẳng định nào sau đây là sai?
. Khẳng định nào sau đây là sai?
Biểu diễn các góc trên đường tròn ta thấy:
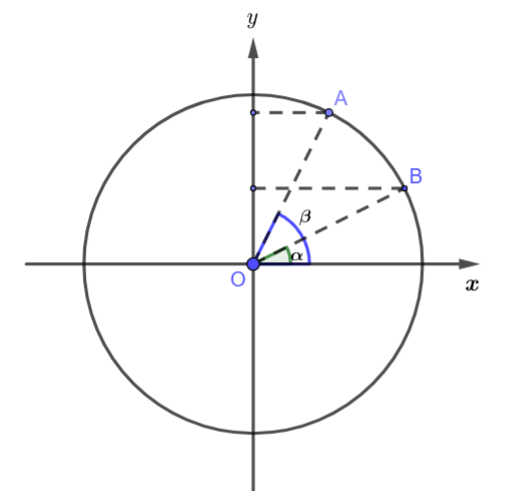
Nhận thấy
Vậy khẳng định sai là: .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
