Giá trị lượng giác của một góc từ 0 đến 180 độ
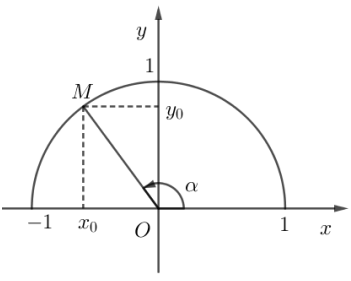
Trong mặt phẳng tọa độ 
\(Oxy\), nửa đường tròn tâm \(O\) nằm phía trên trục hoành có bán kính \(R=1\) được gọi là nửa đường tròn đơn vị.
Với mỗi góc \(\alpha\) (\(0^{\circ} \le \alpha \le 180^{\circ}\)) ta xác định một điểm \(M\) trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha\) và điểm \(M\) có tọa độ \(M(x_0;y_0)\). Khi đó:
- \(\sin\) của góc \(\alpha\) là \(y_0\), kí hiệu \(\sin \alpha = {y_0}\).
- côsin của góc \(\alpha\) là \(x_0\), kí hiệu \(\cos \alpha =x_0\).
- tang của góc \(\alpha\) là \(\frac{y_0}{x_0}\) (\(x_0 \neq 0\)), kí hiệu \(\tan \alpha = \frac{y_0}{x_0}\).
- côtang của góc \(\alpha\) là \(\frac {x_0}{y_0}\) (\(y_0 \neq 0\)), kí hiệu \(\cot \alpha = \frac {x_0}{y_0}\).
Các số \(\sin \alpha ; \cos \alpha; \tan \alpha ; \cot \alpha\) là các giá trị lượng giác của góc \(\alpha\).
2. Quan hệ giữa các giá trị lượng giác bù nhau
- \(\sin \alpha = \sin (180^{\circ} -\alpha)\)
- \(\cos \alpha = -\cos (180^{\circ} -\alpha)\)
- \(\tan \alpha = -\tan (180^{\circ} -\alpha)\)
- \(\cot \alpha = -\cot (180^{\circ} -\alpha)\)
Ví dụ: Đơn giản hóa các biểu thức sau:
a) \(\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}\);
b) \(-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)\).
Hướng dẫn giải
a) \(\sin 110^{\circ} +\cos 50^{\circ} -\sin70^{\circ} +\cos130^{\circ}\)\(= (\sin 110^{\circ} -\sin70^{\circ}) +(\cos130^{\circ}+\cos 50^{\circ})\)\(= (\sin (180^\circ - 110^{\circ}) -\sin70^{\circ})\)\(+(\cos130^{\circ}-\cos (180^{\circ} -50^{\circ}))\)\(=(\sin 70^{\circ} -\sin 70^{\circ} )+(\cos 130^{\circ} -\cos 130^{\circ} )=0\).
b) \(-2\sin (180^{\circ} -\beta).\cot \beta + 3\cos \beta +\cos(180^{\circ} -\beta)\)=\(-2\sin \beta.\cot \beta + 3\cos \beta -\cos\beta\)\(-2\sin \beta. \frac {\cos\beta} {\sin \beta} + 3\cos \beta -\cos\beta =\)\(-2\cos\beta + 3\cos \beta -\cos\beta=0\).
3. Giá trị lượng giác của các góc đặc biệt
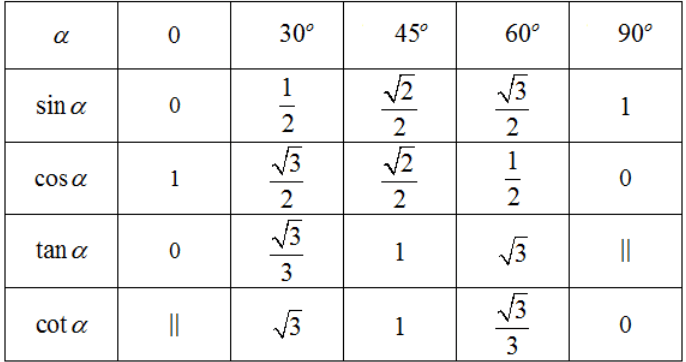
Chú ý: Trong bảng trên, kí hiệu || để chỉ các giá trị lượng giác không xác định.
Ví dụ: Cho góc \(\alpha\) (\(0^{\circ} < \alpha <180^{\circ}\)) thỏa mãn \(\tan \alpha =2\). Hãy tính giá trị biểu thức \(S= \frac {3\sin\alpha +2\cos\alpha}{2\sin\alpha -3\cos\alpha}\).
Hướng dẫn giải
Vì \(\tan \alpha =\frac {\sin\alpha}{\cos\alpha}\) nên:
Chia cả tử cả mẫu cho \(\cos\alpha\), ta được: \(S= \frac {3\tan\alpha +2}{2\tan\alpha -3}\)\(= \frac {3.2+2}{2.2 -3}=8\).
