Tổng và hiệu của hai vectơ
Cho hai vectơ ![]() \(\overrightarrow a\) và
\(\overrightarrow a\) và ![]() \(\overrightarrow b\). Lấy một điểm
\(\overrightarrow b\). Lấy một điểm ![]() \(A\) rồi xác định các điểm
\(A\) rồi xác định các điểm ![]() \(B,C\) sao cho
\(B,C\) sao cho ![]() \(\overrightarrow {AB}=\overrightarrow {a},\overrightarrow {BC}=\overrightarrow {b}\). Khi đó vectơ
\(\overrightarrow {AB}=\overrightarrow {a},\overrightarrow {BC}=\overrightarrow {b}\). Khi đó vectơ ![]() \(\overrightarrow {AC}\) được gọi là tổng của hai vectơ
\(\overrightarrow {AC}\) được gọi là tổng của hai vectơ ![]() \(\overrightarrow a\) và
\(\overrightarrow a\) và ![]() \(\overrightarrow b\).
\(\overrightarrow b\).
- Kí hiệu:
 \(\overrightarrow {AC}=\overrightarrow a+\overrightarrow b\).
\(\overrightarrow {AC}=\overrightarrow a+\overrightarrow b\). - Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.
Tính chất:
- Tính chất giao hoán:
 \(\overrightarrow a+\overrightarrow b=\overrightarrow b+\overrightarrow a .\)
\(\overrightarrow a+\overrightarrow b=\overrightarrow b+\overrightarrow a .\) - Tính chất kết hợp:
 \((\overrightarrow a+\overrightarrow b)+\overrightarrow c=\overrightarrow a+(\overrightarrow b+\overrightarrow c) .\)
\((\overrightarrow a+\overrightarrow b)+\overrightarrow c=\overrightarrow a+(\overrightarrow b+\overrightarrow c) .\) - Tính chất của vectơ - không:
 \(\overrightarrow a +\overrightarrow 0=\overrightarrow a .\)
\(\overrightarrow a +\overrightarrow 0=\overrightarrow a .\)
Các quy tắc quan trọng
- Quy tắc ba điểm: Với ba điểm bất kì
 \(A,B,C\) ta có:
\(A,B,C\) ta có:  \(\overrightarrow {AB} +\overrightarrow {BC}=\overrightarrow {AC}\).
\(\overrightarrow {AB} +\overrightarrow {BC}=\overrightarrow {AC}\). - Quy tắc hình bình hành: Nếu
 \(ABCD\) là hình bình hành thì ta có:
\(ABCD\) là hình bình hành thì ta có:  \(\overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC}\).
\(\overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC}\).
Ghi nhớ
- Nếu
 \(M\) là trung điểm
\(M\) là trung điểm  \(AB\) thì
\(AB\) thì  \(\overrightarrow {MA}+\overrightarrow {MB}=\overrightarrow 0\).
\(\overrightarrow {MA}+\overrightarrow {MB}=\overrightarrow 0\). - Nếu
 \(G\) là trọng tâm tam giác
\(G\) là trọng tâm tam giác  \(ABC\) thì
\(ABC\) thì  \(\overrightarrow {GA}+\overrightarrow {GB}+\overrightarrow {GC}=\overrightarrow 0\).
\(\overrightarrow {GA}+\overrightarrow {GB}+\overrightarrow {GC}=\overrightarrow 0\).
Ví dụ 1: Cho hình chữ nhật ![]() \(ABCD\) với
\(ABCD\) với ![]() \(AB=a,AD=2a\).
\(AB=a,AD=2a\).
a) Tính độ dài vectơ ![]() \(\overrightarrow {AB}+\overrightarrow {AD}\).
\(\overrightarrow {AB}+\overrightarrow {AD}\).
b) Tính độ dài vectơ ![]() \(\overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB}\).
\(\overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB}\).
Hướng dẫn giải
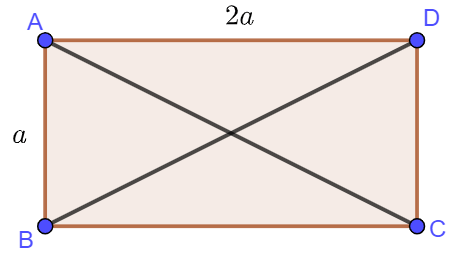
a) Áp dụng quy tắc hình bình hành: ![]() \(\overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC}\) nên
\(\overrightarrow {AB}+\overrightarrow {AD}=\overrightarrow {AC}\) nên ![]() \(\left | \overrightarrow {AB}+\overrightarrow {AD} \right | =\left | \overrightarrow {AC} \right |\).
\(\left | \overrightarrow {AB}+\overrightarrow {AD} \right | =\left | \overrightarrow {AC} \right |\).
Áp dụng định lý Py-ta-go cho tam giác ![]() \(ABC\), ta có:
\(ABC\), ta có: ![]() \(AC=a\sqrt5\).
\(AC=a\sqrt5\).
Vậy ![]() \(\left | \overrightarrow {AB}+\overrightarrow {AD} \right | =\left | \overrightarrow {AC} \right |=a\sqrt5\).
\(\left | \overrightarrow {AB}+\overrightarrow {AD} \right | =\left | \overrightarrow {AC} \right |=a\sqrt5\).
b) Áp dụng quy tắc ba điểm và quy tắc hình bình hành: ![]() \(\overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB}=(\overrightarrow {BD}+\overrightarrow {DC})+\overrightarrow {AB}\)
\(\overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB}=(\overrightarrow {BD}+\overrightarrow {DC})+\overrightarrow {AB}\)![]() \(=\overrightarrow {BC}+\overrightarrow {AB} =\overrightarrow {AD}+\overrightarrow {AB}=\overrightarrow {AC}\).
\(=\overrightarrow {BC}+\overrightarrow {AB} =\overrightarrow {AD}+\overrightarrow {AB}=\overrightarrow {AC}\).
Do đó: ![]() \(\left | \overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB} \right | =\left | \overrightarrow {AC} \right | =a\sqrt5\).
\(\left | \overrightarrow {DC}+\overrightarrow {BD}+\overrightarrow {AB} \right | =\left | \overrightarrow {AC} \right | =a\sqrt5\).
Ví dụ 2: Cho tam giác ![]() \(ABC\) đều cạnh bằng
\(ABC\) đều cạnh bằng ![]() \(1\). Tính
\(1\). Tính ![]() \(\left | \overrightarrow {AB}+\overrightarrow {AC} \right |\).
\(\left | \overrightarrow {AB}+\overrightarrow {AC} \right |\).
Hướng dẫn giải
Lấy ![]() \(D\) là điểm thỏa mãn tứ giác
\(D\) là điểm thỏa mãn tứ giác ![]() \(ABDC\) là hình bình hành. Vì
\(ABDC\) là hình bình hành. Vì ![]() \(AB=AC\) nên suy ra
\(AB=AC\) nên suy ra ![]() \(ABDC\) là hình thoi. Gọi tâm hình thoi là
\(ABDC\) là hình thoi. Gọi tâm hình thoi là ![]() \(O\).
\(O\).
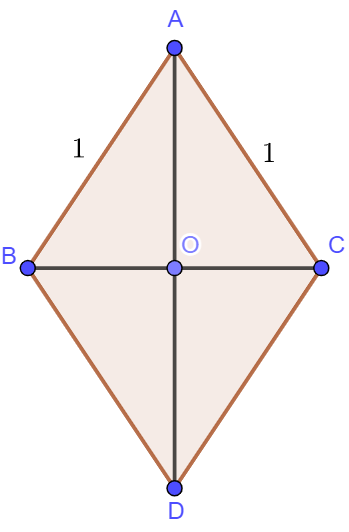
Áp dụng quy tắc hình bình hành: ![]() \(\left | \overrightarrow {AB}+\overrightarrow {AC} \right | =\left | \overrightarrow {AD} \right | =AD=2AO .\)
\(\left | \overrightarrow {AB}+\overrightarrow {AC} \right | =\left | \overrightarrow {AD} \right | =AD=2AO .\)
Xét tam giác vuông ![]() \(AOB\), ta có:
\(AOB\), ta có: ![]() \(AO^2=AB^2-BO^2 \Leftrightarrow AO^2=1^2-(\frac12)^2\)
\(AO^2=AB^2-BO^2 \Leftrightarrow AO^2=1^2-(\frac12)^2\)![]() \(\Leftrightarrow AO=\frac{\sqrt3}2 .\)
\(\Leftrightarrow AO=\frac{\sqrt3}2 .\)
Suy ra: ![]() \(\left | \overrightarrow {AB}+\overrightarrow {AC} \right | =\left | \overrightarrow {AD} \right | =AD\)
\(\left | \overrightarrow {AB}+\overrightarrow {AC} \right | =\left | \overrightarrow {AD} \right | =AD\)![]() \(=2AO=\frac{\sqrt3}2.2=\sqrt3 .\)
\(=2AO=\frac{\sqrt3}2.2=\sqrt3 .\)
2. Hiệu của hai vectơ
- Hiệu hai vectơ
 \(\overrightarrow a\) và
\(\overrightarrow a\) và  \(\overrightarrow b\), kí hiệu là
\(\overrightarrow b\), kí hiệu là  \(\overrightarrow a - \overrightarrow b\), là tổng của vectơ
\(\overrightarrow a - \overrightarrow b\), là tổng của vectơ  \(\overrightarrow a\) và vectơ đối của vectơ
\(\overrightarrow a\) và vectơ đối của vectơ  \(\overrightarrow b\), tức là
\(\overrightarrow b\), tức là  \(\overrightarrow a - \overrightarrow b=\overrightarrow a+ (-\overrightarrow b) .\)
\(\overrightarrow a - \overrightarrow b=\overrightarrow a+ (-\overrightarrow b) .\) - Phép lấy hiệu của hai vectơ gọi là phép trừ vectơ.
Quy tắc về hiệu vectơ
- Nếu
 \(\overrightarrow {MN}\) là một vectơ đã cho thì với điểm
\(\overrightarrow {MN}\) là một vectơ đã cho thì với điểm  \(O\) bất kì, ta luôn có:
\(O\) bất kì, ta luôn có:  \(\overrightarrow {MN}=\overrightarrow {ON}-\overrightarrow {OM} .\)
\(\overrightarrow {MN}=\overrightarrow {ON}-\overrightarrow {OM} .\)
Ví dụ: Cho tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(A\) có
\(A\) có ![]() \(AB=1,AC=2\). Tính độ dài vectơ
\(AB=1,AC=2\). Tính độ dài vectơ ![]() \(\overrightarrow {AB}-\overrightarrow {AC}\).
\(\overrightarrow {AB}-\overrightarrow {AC}\).
Hướng dẫn giải
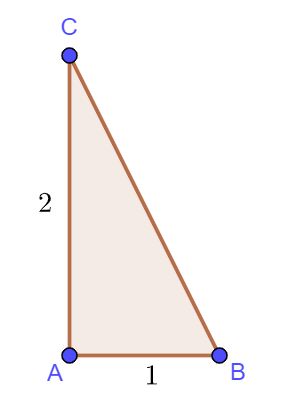
Áp dụng quy tắc hiệu của hai vectơ: ![]() \(\left | \overrightarrow {AB}-\overrightarrow {AC} \right | =\left | \overrightarrow {CB} \right | =CB .\)
\(\left | \overrightarrow {AB}-\overrightarrow {AC} \right | =\left | \overrightarrow {CB} \right | =CB .\)
Áp dụng định lý Py-ta-go: ![]() \(BC=\sqrt{AB^2+BC^2}=\sqrt{1^2+2^2}=\sqrt5\).
\(BC=\sqrt{AB^2+BC^2}=\sqrt{1^2+2^2}=\sqrt5\).
Vậy ![]() \(\left | \overrightarrow {AB}-\overrightarrow {AC} \right | =\left | \overrightarrow {CB} \right | =CB =\sqrt5 .\)
\(\left | \overrightarrow {AB}-\overrightarrow {AC} \right | =\left | \overrightarrow {CB} \right | =CB =\sqrt5 .\)





