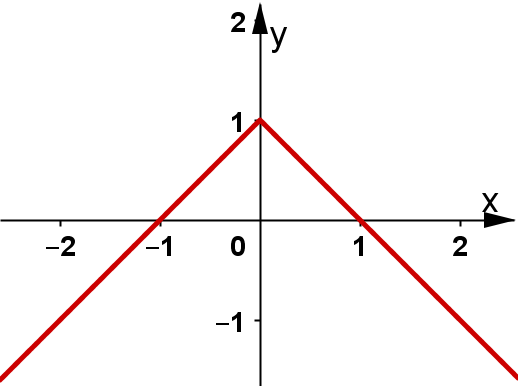
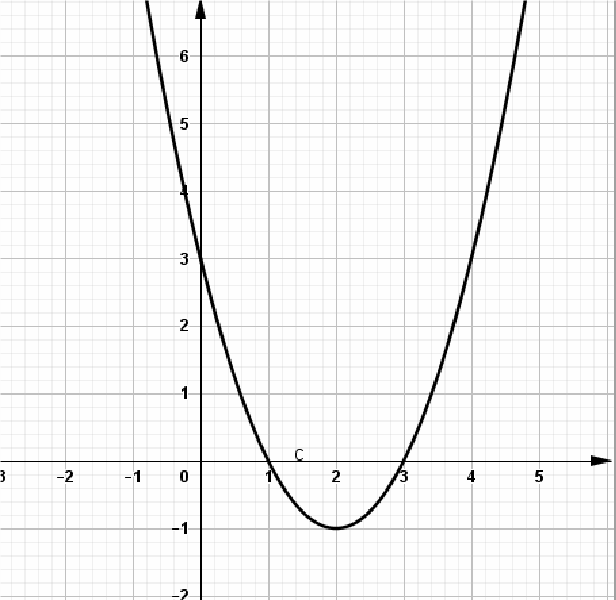
Cho hàm số y = f(x) có tập xác định là [ − 1; 3] và đồ thị của nó được biểu diễn bởi hình bên.
Khẳng định nào sau đây là sai?
Trên khoảng (0;2) đồ thị hàm số đi ngang từ trái sang phải
Hàm số không đổi trên khoảng (0;2).
Trên khoảng (2;3) đồ thị hàm số đi lên từ trái sang phải
Hàm số đồng biến trên khoảng (2;3).
Chọn đáp án Hàm số đồng biến trên khoảng (2;3).