Phương trình đường thẳng
- Vectơ
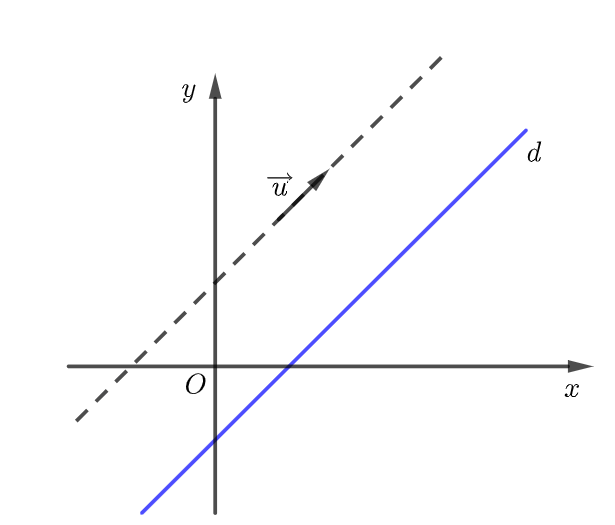
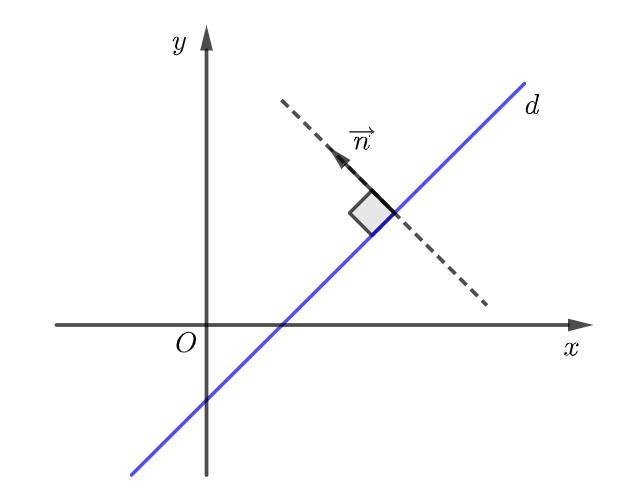
\(\overrightarrow u\) được gọi là vectơ chỉ phương của đường thẳng \(d\) nếu \(\overrightarrow u\) có giá song song hoặc trùng với đường thẳng \(d\). - Vectơ \(\overrightarrow u\) được gọi là vectơ pháp tuyến của đường thẳng \(d\) nếu \(\overrightarrow u\) có giá vuông góc với đường thẳng \(d\).
Nhận xét:
- Một đường thẳng được xác định khi biết 1 điểm và 1 vectơ chỉ phương hoặc 1 điểm và 1 vectơ pháp tuyến.
- Một đường thẳng có vô số vectơ chỉ phương, chúng cùng phương với nhau. (Tức là nếu \(\overrightarrow u\) là một vectơ chỉ phương thì \(k\overrightarrow u (k\neq0)\) cũng là một vectơ chỉ phương).
- Một đường thẳng có vô số vectơ pháp tuyến, chúng cùng phương với nhau . (Tức là nếu \(\overrightarrow n\) là một vectơ pháp tuyến thì \(k\overrightarrow n(k\neq0)\) cũng là một vectơ pháp tuyến).
- Nếu \(\overrightarrow u(a;b)\) là một vectơ chỉ phương của \(d\) thì \(\overrightarrow n(-b;a)\) là một vectơ pháp tuyến của \(d.\)
Ví dụ: Cho hai điểm \(A(1;0)\) và \(B(-1;3)\). Tìm một vectơ chỉ phương và một vectơ pháp tuyến của đường thẳng \(AB\).
Hướng dẫn giải
Ta có: \(\overrightarrow {AB}( -2;3)\) là một vectơ chỉ phương của đường thẳng \(AB\).
Vì \(\overrightarrow {AB}( -2;3)\)là một vectơ chỉ phương của đường thẳng \(AB\). Suy ra \(\overrightarrow n_{AB}=(3;2)\) là một vectơ pháp tuyến của đường thẳng \(AB\).
2. Phương trình tổng quát của đường thẳng
Cho đường thẳng \(d\) đi qua điểm \(M(x_0;y_0)\) và nhận vectơ \(\overrightarrow n(a;b)\neq\overrightarrow0\) làm vectơ pháp tuyến. Khi đó, phương trình tổng quát của \(d\) có dạng:
\(a(x-x_0)+b(y-y_0)=0\)
Nếu đặt \(c=-ax_0-by_0\) thì phương trình tổng quát còn được viết dưới dạng \(ax+by+c=0\).
Nhận xét:
- Cho đường thẳng \(d\) có phương trình tổng quát \(ax+by+c=0\) và một điểm \(A(x_0;y_0)\). Khi đó: Điểm \(A\) thuộc đường thẳng \(d\) khi và chỉ khi \(ax_0+by_0+c=0\). (thay tọa độ \(A\) vào phương trình tổng quát thỏa mãn)
Ví dụ: Trong mặt phẳng tọa độ, cho \(\overrightarrow n(2;3)\) và \(A(1;2);B(-1;1)\).
a. Lập phương trình tổng quát của đường thẳng \(d\) đi qua \(A\) và nhận \(\overrightarrow n\) là vectơ pháp tuyến.
b. Lập phương trình tổng quát của đường thẳng \(AB\).
Hướng dẫn giải
a. Phương trình tổng quát của đường thẳng \(d\) đi qua \(A(1;2)\) và nhận \(\overrightarrow n(2;3)\) là vectơ pháp tuyến có dạng:
\(2(x-1)+3(y-2)=0 \Leftrightarrow 2x+3y-8=0\).
b. Vectơ chỉ phương của đường thẳng \(AB\) là \(\overrightarrow {AB}( -2;-1)\Rightarrow \overrightarrow n_{AB}=(1;-2)\).
Phương trình tổng quát của đường thẳng \(AB\) đi qua \(A(1;2)\) và nhận \(\overrightarrow n_{AB}=(1;-2)\) là vectơ pháp tuyến có dạng:
\(1(x-1)-2(y-2)=0\Leftrightarrow x-2y-5=0\).
3. Phương trình tham số của đường thẳng
Cho đường thẳng \(d\) đi qua điểm \(M(x_0;y_0)\) và nhận vectơ \(\overrightarrow u(a;b)\neq\overrightarrow0\)làm vectơ chỉ phương. Khi đó, phương trình tham số của \(d\) là:
\(d:\left\{ {\begin{array}{*{20}{c}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array}} \right. (t\in\mathbb{R})\)
Ví dụ: Trong mặt phẳng tọa độ, cho \(\overrightarrow u(1;-1)\) và hai điểm \(M(-2;2);N(-3;0)\).
a. Lập phương trình tham số của đường thẳng \(\Delta\) đi qua \(M\) và nhận \(\overrightarrow u(1;-2)\) là vectơ chỉ phương.
b. Lập phương trình tham số của đường thẳng \(MN\).
Hướng dẫn giải
a. Phương trình tham số của đường thẳng \(\Delta\) đi qua \(M(-2;2)\) và nhận \(\overrightarrow u(1;-2)\) là vectơ chỉ phương có dạng là:
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = - 2 + t}\\
{y = 2 - 2t}
\end{array}} \right. (t\in\mathbb{R})\)
b. Vectơ chỉ phương của đường thẳng \(MN\) là \(\overrightarrow {MN}(-1;-2)\).
Phương trình tham số của đường thẳng \(MN\) đi qua điểm \(M(-2;2)\) và nhận \(\overrightarrow {MN}(-1;-2)\) là vectơ chỉ phương có dạng là:
\(MN:\left\{ {\begin{array}{*{20}{c}}
{x = - 2 - t}\\
{y = 2 - 2t}
\end{array}} \right. (t\in\mathbb{R})\)
