VnDoc.com

Đề thi giữa học kì 2 Toán 10 Kết nối tri thức (Đề 4)

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Mô tả thêm:

Cùng nhau ôn tập, thử sức với đề kiểm tra giữa học kì 2 Toán 10 - Kết nối tri thức nha!

Thời gian làm: 90 phút
Số câu hỏi: 40 câu
Số điểm tối đa: 40 điểm
Tài khoản: Đăng nhập

Trước khi làm bài bạn hãy

1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
4 Căn chỉnh thời gian làm từng câu một cách hợp lý

Câu 1: Vận dụng
Tìm bảng biến thiên của tam thức bậc hai

Cho tam thức bậc hai $f(x) = ax^{2} + bx + c$ có đồ thị như hình vẽ dưới đây
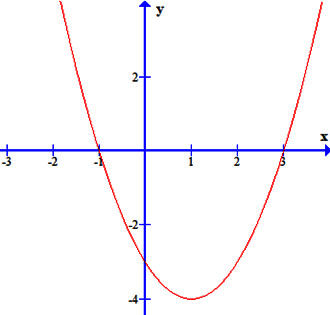
Bảng biến thiên của tam thức bậc hai là
- A.
- B.
- C.
- D.
Từ đồ thị ta có:
Đồ thị hàm số cắt trục hoành tại hai điểm có hoành độ x = – 1 và x = 3
=> f(x) có 2 nghiệm phân biệt là x = –1; x = 3 ta loại các đáp án
Ta lại có: f(x) nhận giá trị dương trên các khoảng (– ∞; –1) và (3; + ∞); f(x) nhận giá trị âm trên khoảng (–1; 3) ta loại đáp án
Vậy bảng biến thiên đúng là
Câu 2: Thông hiểu
Tìm điều kiện của tham số m để phương trình có nghiệm

Tất cả các giá trị của tham số m để phương trình $\frac{3mx + 1}{\sqrt{x + 1}} + \sqrt{x + 1} =\frac{2x + 5m + 3}{\sqrt{x + 1}}$ có nghiệm là:
- A.
  $0 < m <\frac{1}{3}$ .
- B.
  $\left\lbrack \begin{matrix}m < 0 \\m > \frac{1}{3} \\\end{matrix} ight.$ .
- C.
  $- \frac{1}{3} < m <0$ .
- D.
  $\left\lbrack \begin{matrix}m < - \frac{1}{3} \\m > 0 \\\end{matrix} ight.$ .
ĐKXĐ: x > − 1
pt ⇔ 3mx + 1 + x + 1 = 2x + 5m + 3 ⇔ (3m−1)x = 5m + 1.
Phương trình đã cho có nghiệm $\Leftrightarrow \left\{ \begin{matrix}3m - 1 eq 0 \\x = \frac{5m + 1}{3m - 1} > - 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}m eq \frac{1}{3} \\\frac{8m}{3m - 1} > 0 \\\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}m > \frac{1}{3} \\m < 0 \\\end{matrix} ight.$ .
Câu 3: Nhận biết
Tìm tập nghiệm của phương trình

Phương trình $\sqrt{x-1}=x-3$ có tập nghiệm là:
- A.
  {5}
- B.
  {2}
- C.
  {2;5}
- D.
  ∅.
Ta có: $\sqrt{x-1}=x-3 \Rightarrow x-1=x^2-6x+9$ $\Leftrightarrow x^2-7x+10=0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 2}\\{x = 5}\end{array}} ight.$ .
Thử lại $x=2$ thấy không thỏa mãn. Vậy $S=\{5\}$ .
Câu 4: Vận dụng
Chọn khẳng định đúng

Cho hàm số $y = f(x) = x^{3} + \left( m^{2} - 1 ight)x^{2} + 2x + m - 1$ là một hàm số lẻ. Biết rằng $m = m_{0}$ . Khẳng định nào dưới đây là khẳng định đúng?
- A.
  $m_{0} \in \left( \frac{1}{2};3 ight)$
- B.
  $m_{0} \in \left\lbrack - \frac{1}{2};0 ightbrack$
- C.
  $m_{0} \in \left( 0;\frac{1}{2} ightbrack$
- D.
  $m_{0} \in \lbrack 3; + \infty)$
Tập xác định $D\mathbb{= R}$

Với $x \in D \Rightarrow - x \in D$

$f( - x) = ( - x)^{3} + \left( m^{2} - 1 ight).( - x)^{2} + 2( - x) + m - 1$

$= - x^{3} + \left( m^{2} - 1 ight).x^{2} - 2x + m - 1$

Hàm số đã cho là hàm số lẻ khi đó:

$f( - x) = - f(x),\forall x \in D$

$\Leftrightarrow - x^{3} + \left( m^{2} - 1 ight).x^{2} - 2x + m - 1 = - \left\lbrack x^{3} + \left( m^{2} - 1 ight)x^{2} + 2x + m - 1 ightbrack$

$\Leftrightarrow 2\left( m^{2} - 1 ight)x^{2} + 2(m - 1) = 0$

$\Leftrightarrow \left\lbrack \begin{matrix} m^{2} - 1 = 0 \\ m - 1 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} m = \pm 1 \\ m = 1 \\ \end{matrix} ight.\ \Leftrightarrow m = 1$

Vậy $m_{0} = 1 \in \left( \frac{1}{2};3 ight)$

VD

1
Câu 5: Nhận biết
Tìm tọa độ trung điểm I

Trên mặt phẳng tọa độ $Oxy$ cho tọa độ hai điểm $M(1;0),N(7;4)$ . Tọa độ trung điểm $I$ của $MN$ là:
- A.
  $I(4;2)$
- B.
  $I( - 6; - 4)$
- C.
  $I(3;2)$
- D.
  $I(8;4)$
Tọa độ trung điểm I của MN là:

$\left\{ \begin{matrix}x_{I} = \dfrac{x_{M} + x_{N}}{2} \\y_{I} = \dfrac{y_{M} + y_{N}}{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x_{I} = \dfrac{1 + 7}{2} = 4 \\y_{I} = \dfrac{0 + 4}{2} = 2 \\\end{matrix} ight.$

Vậy tọa độ trung điểm của MN là: $I(4;2)$ .
Câu 6: Thông hiểu
Tìm các giá trị nguyên của tham số m

Cho phương trình $x^{2} - mx - m^{2} = 0$ với $m$ là tham số. Có bao nhiêu giá trị nguyên của tham số $m \in \lbrack - 10;10brack$ để phương trình đã cho có hai nghiệm trái dấu?
- A.
  $20$
- B.
  $21$
- C.
  $9$
- D.
  $10$
Từ yêu cầu bài toán

$\Leftrightarrow a.c < 0 \Leftrightarrow - m^{2} < 0 \Leftrightarrow m^{2} > 0 \Leftrightarrow m eq 0$

Suy ra $m \in \left\{ - 10;....; - 1 ight\} \cup \left\{ 1;...;10 ight\}$

Vậy có 20 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 7: Vận dụng cao
Tìm m để diện tích tam giác đạt max

Cho đường tròn $(C):x^{2} + y^{2} - 2x + 4y - 4 = 0$ tâm $I$ và đường thẳng $(\Delta):\sqrt{2}x + my + 1 - \sqrt{2} =0$ cắt nhau tại hai điểm $M;N$ . Tìm giá trị tham số $m$ để diện tích tam giác $MNI$ có giá trị lớn nhất?
- A.
  $m = 3$
- B.
  $m = - 4$
- C.
  $m = 4$
- D.
  $m = - 3$
Hình vẽ minh họa
Đường tròn (C) tâm I(1; -2) bán kính R = 3
Diện tích tam giác MNI là:
$S_{MNI} =\frac{1}{2}IM.IN.sin\widehat{MIN} \leq \frac{1}{2}IM.IN$
Suy ra $\max S_{MNI} = \frac{1}{2}IM.IN =\frac{9}{2}$ đạt được khi tam giác MNI vuông cân tại I và $AB = IA\sqrt{2} = R\sqrt{2} =3\sqrt{2}$
Mặt khác
$S_{MNI} =\frac{1}{2}.MN.d(I,\Delta)$
$\Leftrightarrow \frac{9}{2} =\frac{1}{2}.3\sqrt{2}.d(I,\Delta) \Leftrightarrow d(I,\Delta) =\frac{3}{\sqrt{2}}$
$\Leftrightarrow \frac{\left| \sqrt{2}.1+ m.( - 2) + 1 - \sqrt{2} ight|}{\sqrt{2 + m^{2}}} =\frac{3}{\sqrt{2}}$
$\Leftrightarrow \frac{|1 - 2m|}{\sqrt{2+ m^{2}}} = \frac{3}{\sqrt{2}}$
$\Leftrightarrow 2(1 - 2m)^{2} = 9\left(2 + m^{2} ight)$
$\Leftrightarrow (m + 4)^{2} = 0\Leftrightarrow m = - 4$
Vậy $m = - 4$ thỏa mãn yêu cầu bài toán.
Câu 8: Thông hiểu
Xác định tất cả các giá trị nguyên của tham số m

Có bao nhiêu giá trị nguyên của tham số $m$ sao cho hàm số $x^{2} + (m - 1)x + m - 2 = 0$ có hai nghiệm phân biệt thuộc khoảng $( - 5;5)$ ?
- A.
  $6$
- B.
  $7$
- C.
  $8$
- D.
  $9$
Ta có:

$PT \Leftrightarrow (x + 1)(x + m - 2) = 0$

$\Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = - m + 2 \\ \end{matrix} ight.$

Từ yêu cầu bài toán $\Leftrightarrow \left\{ \begin{matrix} - m + 2 eq - 1 \\ - 5 < - m + 2 < 5 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m eq 3 \\ - 3 < m < 7 \\ \end{matrix} ight.$

Suy ra $m \in \left\{ - 2; - 1;0;1;2;4;5;6 ight\}$

Vậy có 8 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 9: Thông hiểu
Tìm a thỏa mãn điều kiện

Với giá trị nào của a thì ax² − x + a ≥ 0, ∀x ∈ ℝ?
- A.
  a = 0.
- B.
  a < 0.
- C.
  $0 < a \leq \frac{1}{2}$ .
- D.
  $a \geq \frac{1}{2}$ .
*a = 0thì bpt trở thành − x ≥ 0 ⇔ x ≤ 0. Suy ra a = 0không thỏa ycbt.

* a ≠ 0 thì $ax^{2} - x + a \geq 0,\forall x\mathbb{\in R \Leftrightarrow}\left\{ \begin{matrix} \Delta \leq 0 \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} 1 - 4a^{2} \leq 0 \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} a \geq \frac{1}{2} \\ a \leq - \frac{1}{2} \\ \end{matrix} ight.\ \\ a > 0 \\ \end{matrix} ight.\ \Leftrightarrow a \geq \frac{1}{2}$ .
Câu 10: Vận dụng
Cửa hàng bán một đôi giày giá bao nhiêu

Một của hàng buôn giày nhập một đôi với giá là 40 USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua (120−x) đôi. Hỏi cửa hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
- A.
  80 USD
- B.
  160 USD
- C.
  40 USD
- D.
  240 USD
Gọi y là số tiền lãi của cửa hàng bán giày.

Ta có y = (120−x)(x−40) = − x² + 160x − 4800 = − (x−80)² + 1600 ≤ 1600.

Dấu $" = "$ xảy ra ⇔ x = 80.

Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD.
Câu 11: Thông hiểu
Có bao nhiêu số tự nhiên được tạo thành

Từ tập hợp các chữ số $A = \left\{ 1,2,3,4,5,6 ight\}$ có thể lập được bao nhiêu số có ba chữ số khác nhau thuộc khoảng $(300;500)$ ?
- A.
  $720$ số
- B.
  $40$ số
- C.
  $20$ số
- D.
  $41$ số
Gọi số tự nhiên có ba chữ số cần tìm có dạng $\overline{abc};(a eq 0)$

Số cần tìm thuộc khoảng $(300;500)$ nên $a \in \left\{ 3;4 ight\}$ => a có 2 cách chọn.

Số cách chọn b là 5 cách chọn

Số cách chọn c là 4 cách chọn

Vậy có thể lập được $2.5.4 = 40$ (số) thỏa mãn yêu cầu đề bài.
Câu 12: Thông hiểu
Tính số cách chọn học sinh

Một nhóm học sinh gồm 7 học sinh nam và 4 học sinh nữ. Chọn ngẫu nhiên 1 bạn nam và 1 bạn nữ để trực nhật lớp. Hỏi có bao nhiêu cách chọn?
- A.
  $32$
- B.
  $11$
- C.
  $28$
- D.
  $2$
Số cách chọn một bạn nam là: $7$ cách
Số cách chọn một bạn nữ là: $4$ cách
Vậy số cách chọn 1 nam, 1 nữ đi trực nhật lớp là: $7.4 = 28$ cách chọn.
Câu 13: Thông hiểu
Giải phương trình

Giá trị của $x$ thoả mãn phương trình $A_{x}^{10}+ A_{x}^{9}=9A_{x}^{8}$ là:
- A.
  $x = 10$
- B.
  $x = 9$
- C.
  $x = 11$
- D.
  $x = 12$
Điều kiện: $x \ge10$ .
Thay $x=11$ vào phương trình, ta được: $A_{11}^{10} + A_{11}^9 = 9A_{11}^8$ (2 vế bằng nhau). Do đó $x=11$ là nghiệm của phương trình.
Câu 14: Nhận biết
Tính khoảng cách từ A đến đường thẳng d

Trong mặt phẳng $Oxy$ cho điểm $A(4; - 5)$ và đường thẳng $(d):3.x - 4y + 8 = 0$ . Tính khoảng cách từ điểm A đến đường thẳng (d).
- A.
  $9$
- B.
  $8$
- C.
  $7$
- D.
  $6$
Khoảng cách từ điểm A đến đường thẳng (d) là:

$d\left( A;(d) ight) = \frac{\left| 3.4 - 4.( - 5) + 8 ight|}{\sqrt{3^{2} + 4^{2}}} = 8$

Vậy khoảng cách cần tìm bằng 8.
Câu 15: Thông hiểu
Tìm m để hai đường thẳng vuông góc

Trong mặt phẳng tọa độ $Oxy$ , cho hai đường thẳng $\left( d_{1} ight):mx - (m - 1)y + 4 - m^{2} = 0$ và $\left( d_{2} ight):(m + 3)x + y - 3m - 1 = 0$ . Tìm giá trị của tham số $m$ để hai đường thẳng hợp với nhau một góc bằng một góc vuông?
- A.
  $m = 2$
- B.
  $m = 0$
- C.
  $m = 1$
- D.
  $m = - 1$
Ta có:

Vectơ pháp tuyến của đường thẳng $\left( d_{1} ight):mx - (m - 1)y + 4 - m^{2} = 0$ là: $\overrightarrow{n_{1}} = (m, - m + 1)$

Vectơ pháp tuyến của đường thẳng $\left( d_{2} ight):(m + 3)x + y - 3m - 1 = 0$ là: $\overrightarrow{n_{2}} = (m + 1;1)$

Hai đường thẳng $\left( d_{1} ight);\left( d_{2} ight)$ vuông góc với nhau khi và chỉ khi:

$\overrightarrow{n_{1}}.\overrightarrow{n_{2}} = 0 \Leftrightarrow m(m + 3) - m + 1 = 0$

$\Leftrightarrow m = - 1$

Vậy hai đường thẳng vuông góc với nhau khi và chỉ khi $m = - 1$ .
Câu 16: Thông hiểu
Tìm tập nghiệm S

Tập nghiệm của phương trình $\frac{x^{2}-5x}{\sqrt{x-2}}+\frac{4}{\sqrt{x-2}} =0$ là:
- A.
  $S=\{1;4\}$
- B.
  $S=\{1\}$
- C.
  $S=\varnothing$
- D.
  $S=\{4\}$
Điều kiện $x>2$ .
Ta có: $\frac{x^{2}-5x}{\sqrt{x-2}}+\frac{4}{\sqrt{x-2}} =0\Leftrightarrow x^2-5x+4=0$ $\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 1}\\{x = 4}\end{array}} ight.$ .
Loại $x=1$ . Do đó $S=\{4\}$ .
Câu 17: Thông hiểu
Tìm m thỏa mãn điều kiện

Với giá trị nào của $m$ thì hai đường thẳng $d_{1}:(m - 3)x + 2y + m^{2} - 1 = 0$ và $d_{2}: - x + my + m^{2} - 2m + 1 = 0$ cắt nhau?
- A.
  $m eq 1$ .
- B.
  $\left\{ \begin{matrix} m eq 1 \\ m eq 2 \\ \end{matrix} ight.$ .
- C.
  $m eq 2$ .
- D.
  $\left\lbrack \begin{matrix} m eq 1 \\ m eq 2 \\ \end{matrix} ight.$ .
$\left\{ \begin{matrix} d_{1}:(m - 3)x + 2y + m^{2} - 1 = 0 \\ d_{2}: - x + my + m^{2} - 2m + 1 = 0 \\ \end{matrix} ight.$

$\overset{d_{1} \cap d_{2} =M}{ightarrow}\left\lbrack \begin{matrix}m = 0 ightarrow \left\{ \begin{matrix}d_{1}: - 3x + 2y - 1 = 0 \\d_{2}: - x + 1 = 0 \\\end{matrix} ight.\ ightarrow TM \\meq0 ightarrow \frac{m - 3}{- 1}eq\frac{2}{m}\Leftrightarrow \left\{ \begin{matrix}meq1 \\meq2 \\\end{matrix} ight.\ \\\end{matrix} ight.\ .$

Chọn $\left\{ \begin{matrix} m eq 1 \\ m eq 2 \\ \end{matrix} ight.$ .
Câu 18: Thông hiểu
Chọn nhận xét đúng

Quan sát đồ thị hàm số, chọn nhận xét đúng?
- A.
  $a > 0,b < 0,c > 0$
- B.
  $a > 0,b > 0,c > 0$
- C.
  $a > 0,b = 0,c > 0$
- D.
  $a < 0,b < 0,c > 0$
Quan sát đồ thị ta thấy có bề lõm quay lên trên suy ra a > 0

Parabol cắt trục tung tại điểm có tọa độ $(0;c)$ nằm phía trên trục hoành nên $c > 0$ .

Đỉnh parabol nằm bên trái trục tung nên có hoành độ $- \frac{b}{2a} < 0$ mà $a > 0$ suy ra $b > 0$ .

Kết luận: $a > 0,b > 0,c > 0$ .
Câu 19: Nhận biết
Tam thức bậc hai dương khi và chỉ khi

Tam thức bậc hai f(x) = 2x² + 2x + 5 nhận giá trị dương khi và chỉ khi
- A.
  x ∈ (0;+∞).
- B.
  x ∈ (−2;+∞).
- C.
  x ∈ ℝ..
- D.
  x ∈ (−∞;2).
f(x) = 2x² + 2x + 5 = 0 có: $\left\{ \begin{matrix} \Delta' = 1 - 10 = - 9 < 0 \\ a = 2 > 0 \\ \end{matrix} ight.$ nên f(x) > 0∀x ∈ ℝ.
Câu 20: Vận dụng cao
Viết phương trình đường thẳng BC

Trong mặt phẳng tọa độ $Oxy$ , cho tam giác $ABC$ có tọa độ $A(1;2)$ . Biết phương trình đường trung tuyến $BM:x + 2y - 2 = 0$ và đường cao $BH:2x + y = 0$ . Xác định phương trình tổng quát của đường thẳng $BC$ ?
- A.
  $5x - 8y - 14 = 0$
- B.
  $5x + 8y + 14 = 0$
- C.
  $5x - 8y + 14 = 0$
- D.
  $- 5x + 8y + 14 = 0$
Tọa độ đỉnh $B = BH \cap BM \Rightarrow B\left( - \frac{2}{3};\frac{4}{3} ight)$

Phương trình đường thẳng AC đi qua điểm $A(1;2)$ và vuông góc với đường thẳng BH là: $x - 2y + 3 = 0$

Tọa độ $M = AC \cap BM \Rightarrow M\left( - \frac{1}{2};\frac{5}{4} ight)$

Vì BM là đường trung tuyến nên M là trung điểm cạnh AC suy ra $C\left( - 2;\frac{1}{2} ight)$

Ta có: $\overrightarrow{BC} = \left( - \frac{4}{3}; - \frac{5}{6} ight)$ là VTCP $\Rightarrow \overrightarrow{n} = (5; - 8)$ là VTPT

Khi đó đường thẳng BC có phương trình là: $5x - 8y + 14 = 0$ .

VDC

1
Câu 21: Nhận biết
Tìm hàm số bậc hai

Trong các hàm số sau, hàm số nào là hàm số bậc hai?
- A.
  $y = 2x + 1$
- B.
  $y = x^{2} + 2x – 1$
- C.
  $y = x^{3} – 1$
- D.
  $y = 1$
Đáp án $y = x^{2} + 2x – 1$ là đáp án đúng vì hàm số bậc hai có dạng $y = a{x^2} + bx + c;\left( {a e 0} ight)$
Câu 22: Thông hiểu
Tính góc giữa hai đường thẳng

Trong mặt phẳng tọa độ $Oxy$ , cho đường thẳng $(d):3x + y - 6 = 0$ và đường thẳng $\Delta:\left\{ \begin{matrix} x = - t \\ y = 5 - 2t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$ . Xác định số đo góc giữa hai đường thẳng đã cho?
- A.
  $30^{0}$
- B.
  $90^{0}$
- C.
  $135^{0}$
- D.
  $45^{0}$
Vectơ pháp tuyến của đường thẳng d và $\Delta$ lần lượt là $\overrightarrow{n_{d}} = (3;1);\overrightarrow{n_{\Delta}} = (2; - 1)$ .

Khi đó góc giữa hai đường thẳng là:

$\cos(d;\Delta) = \frac{\left| \overrightarrow{n_{d}}.\overrightarrow{n_{\Delta}} ight|}{\left| \overrightarrow{n_{d}} ight|.\left| \overrightarrow{n_{\Delta}} ight|} = \frac{|3.2 - 1.1|}{\sqrt{3^{2} + 1^{2}}.\sqrt{2^{2} + ( - 1)^{2}}} = \frac{\sqrt{2}}{2}$

$\Rightarrow (d;\Delta) = 45^{0}$

Vậy góc giữa hai đường thẳng là $45^{0}$ .
Câu 23: Nhận biết
Chọn đáp án đúng

Tính số chỉnh hợp chập 2 của 5 là:
- A.
  $C_{5}^{2}$
- B.
  $A_{5}^{2}$
- C.
  $P_{2}$
- D.
  $5!$
Số chỉnh hợp chập 2 của 5 là: $A_{5}^{2}$ .
Câu 24: Nhận biết
Tính số cách chọn học sinh

Một nhóm học sinh gồm 5 bạn nam và 6 bạn nữ. Hỏi số cách chọn một học sinh bất kì trong nhóm?
- A.
  $5$
- B.
  $11$
- C.
  $30$
- D.
  $6$
Số cách chọn một học sinh bất kì trong nhóm là: 5 + 6 = 11 cách chọn.
Câu 26: Nhận biết
Tìm tam thức bậc hai thỏa mãn

Tam thức nào sau đây nhận giá trị âm với x < 2
- A.
  x² − 5x + 6.
- B.
  16 − x².
- C.
  x² − 2x + 3.
- D.
  − x² + 5x − 6.
Bảng xét dấu của − x² + 5x − 6
Câu 27: Thông hiểu
Tính tổng tất cả các nghiệm của phương trình

Tính tổng tất cả các nghiệm của phương trình $\sqrt{6 - 5x} = 2 - x$ ?
- A.
  $- 1$
- B.
  $1$
- C.
  $2$
- D.
  $0$
Ta có:

$\sqrt{6 - 5x} = 2 - x$

$\Rightarrow \left\{ \begin{matrix} 2 - x \geq 0 \\ 6 - 5x = (2 - x)^{2} \\ \end{matrix} ight.$

$\Leftrightarrow \left\{ \begin{matrix} x \leq 2 \\ x^{2} + x - 2 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x \leq 2 \\ \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.$

Vậy tổng các nghiệm của phương trình bằng $1 + ( - 2) = - 1$ .
Câu 28: Thông hiểu
Tính số cách chọn 4 học sinh

Một nhóm gồm 15 học sinh nam trong đó có 5 bạn giỏi Toán và 20 học sinh nữ trong đó có 6 bạn giỏi Văn. Có bao nhiêu cách chọn 4 học sinh sao cho có đúng 1 học sinh nam giỏi môn Toán và 1 học sinh nữ giỏi môn Văn?
- A.
  $30.C_{26}^{2}$ cách
- B.
  $25.C_{26}^{2}$ cách
- C.
  $2C_{35}^{4}$ cách
- D.
  $C_{26}^{2} + C_{9}^{2}$ cách
Số cách chọn một học sinh nam giỏi Toán và 1 học sinh nữ giỏi Văn là: $C_{5}^{1}.C_{6}^{1} = 30$ (cách)

Chọn 2 học sinh còn lại là: $C_{26}^{2}$ (cách)

Số cách chọn 4 học sinh thỏa mãn là: $30.C_{26}^{2}$ cách.
Câu 29: Thông hiểu
Tìm tập xác định

Tìm tập xác định D của hàm số $f(x) = \sqrt{x + 1} + \frac{1}{x}$ .
- A.
  D = ℝ ∖ {0}
- B.
  D = [1; + ∞)
- C.
  D = ℝ ∖ {−1; 0}
- D.
  D = [ − 1; + ∞) ∖ {0}
Điều kiện: $\left\{ \begin{matrix} x + 1 \geq 0 \\ x eq 0 \\ \end{matrix} ight.$ .

Vậy tập xác định của hàm số là D = [ − 1; + ∞) ∖ {0}.
Câu 30: Nhận biết
Tìm tập nghiệm của bất phương trình

Tập nghiệm của bất phương trình: $2x^{2}–7x–15≥0$ là:
- A.
  $(-\infty ;-\frac{3}{2}]\cup [5;+\infty )$
- B.
  $[-\frac{3}{2};5]$
- C.
  $(-\infty ;5]\cup [\frac{3}{2};+\infty )$
- D.
  $[-5;\frac{3}{2}]$
Ta có: $2x^{2}–7x–15≥0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \le - \frac{3}{2}}\\{x \ge 5}\end{array}} ight.$ .
Vậy $D=(-\infty ;-\frac{3}{2}]\cup [5;+\infty )$ .
Câu 31: Nhận biết
Tính số khả năng lựa chọn chủ đề

Trong một cuốc thi hùng biện, ban tổ chức đã công bố danh sách các chủ đề cho thí sinh gồm 8 chủ đề về lịch sử, 7 chủ đề môi trường, 10 chủ đề về con người và 6 chủ đề về văn hóa. Mỗi thí sinh tham gia thi chỉ được thi với 1 chủ đề. Hỏi mỗi thí sinh có bao nhiêu khả năng lựa chọn chủ đề?
- A.
  $15$
- B.
  $20$
- C.
  $31$
- D.
  $56$
Số cách chọn chủ đề thi của mỗi thí sinh là: 8 + 7 + 10 + 6 = 31.
Câu 32: Nhận biết
Tìm mệnh đề sai

Chọn mệnh đề sai? Đường thẳng $(\Delta)$ được xác định khi biết
- A.
  một vectơ pháp tuyến hoặc một vectơ chỉ phương.
- B.
  hệ số góc và một điểm thuộc $(\Delta)$ .
- C.
  một điểm thuộc $(\Delta)$ và biết $(\Delta)$ song song với một đường thẳng $(d)$ cho trước.
- D.
  hai điểm phân biệt thuộc $(\Delta)$ .
Mệnh đề sai là: “một vectơ pháp tuyến hoặc một vectơ chỉ phương.”
Câu 33: Thông hiểu
Chọn đáp án đúng

Viết phương trình tham số của đường thẳng $\Delta$ có phương trình $x - 3y + 2 = 0$ ?
- A.
  $\left\{ \begin{matrix} x = - 2 + 3t \\ y = t \\ \end{matrix} ight.$
- B.
  $\left\{ \begin{matrix} x = 2 + 3t \\ y = t \\ \end{matrix} ight.$
- C.
  $\left\{ \begin{matrix} x = 2 + t \\ y = - 3t \\ \end{matrix} ight.$
- D.
  $\left\{ \begin{matrix} x = - 2 + t \\ y = - 3t \\ \end{matrix} ight.$
Đường thẳng $\Delta:x - 3y + 2 = 0$ đi qua điểm $A( - 2;0)$ và có vectơ pháp tuyến là $\overrightarrow{n} = (1; - 3)$ nên có vectơ chỉ phương là: $\overrightarrow{u} = (3;1)$ .

Vậy phương trình tham số của $\Delta$ là: $\left\{ \begin{matrix} x = - 2 + 3t \\ y = t \\ \end{matrix} ight.$ .
Câu 34: Thông hiểu
Viết phương trình tham số của đường thẳng

Phương trình tham số của đường thẳng đi qua hai điểm $C(1; - 1),D(2;5)$ là:
- A.
  $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- B.
  $\left\{ \begin{matrix} x = 2t \\ y = - 6t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- C.
  $\left\{ \begin{matrix} x = 2 + t \\ y = 5 + 6t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
- D.
  $\left\{ \begin{matrix} x = 1 \\ y = 2 + 6t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$
Gọi d là đường thẳng qua C và nhận $\overrightarrow{u} = \overrightarrow{CD} = (0;6)$ làm vectơ chỉ phương.

Khi đó phương trình tham số của đường thẳng d là: $\left\{ \begin{matrix} x = 2 \\ y = - 1 + 6t \\ \end{matrix} ight.\ ;\left( t\mathbb{\in R} ight)$ .
Câu 35: Nhận biết
Chọn đáp án đúng

Cho đường thẳng $\Delta:x - 2y - 1 = 0$ . Đường thẳng nào sau đây vuông góc với đường thẳng $\Delta$ ?
- A.
  $2x - y - 2 = 0$
- B.
  $4x + 2y + 3 = 0$
- C.
  $x + 2y - 1 = 0$
- D.
  $x - 2y - 5 = 0$
Đường thẳng $d:4x + 2y + 3 = 0$ vuông góc với đường thẳng $\Delta$ vì $\overrightarrow{n_{d}}.\overrightarrow{n_{\Delta}} = 4.1 + 2( - 2) = 0$ .
Câu 36: Nhận biết
Tìm hàm số thỏa mãn điều kiện

Đồ thị của hàm số nào sau đây là parabol có đỉnh I(−1; 3).
- A.
  y = 2x² + 4x − 3.
- B.
  y = x² − x + 1.
- C.
  y = 2x² + 4x + 5.
- D.
  y = 2x² − 2x − 1.
Đỉnh Parabol là $I\left( - \frac{b}{2a};\ - \frac{\Delta}{4a} ight) = \left( - \frac{b}{2a};\ - \frac{b^{2} - 4ac}{4a} ight)$ .

Do đó chỉ có đáp án y = 2x² + 4x + 5 thỏa mãn.
Câu 37: Nhận biết
Tìm điểm thuộc đồ thị

Điểm nào sau đây thuộc đồ thị của hàm số $y = \frac{x - 2}{x(x - 1)}$ ?
- A.
  M(0;−1).
- B.
  M(2;1).
- C.
  M(2;0).
- D.
  M(1;1).
Thử trực tiếp thấy tọa độ của M(2;0) thỏa mãn phương trình hàm số.
Câu 38: Nhận biết
Chọn công thức đúng

Trong mặt phẳng hệ trục tọa độ $Oxy$ , cho đường thẳng $d$ cắt hai trục $Ox,Oy$ lần lượt tại điểm $A(a;0),B(0;b)$ với $a eq 0;b eq 0$ . Khi đó phương trình đường thẳng $d$ là:
- A.
  $\frac{x}{a} + \frac{y}{b} = 0$
- B.
  $\frac{x}{a} - \frac{y}{b} = 1$
- C.
  $\frac{x}{a} + \frac{y}{b} = 1$
- D.
  $\frac{x}{b} + \frac{y}{a} = 1$
Phương trình đường thẳng d là: $\frac{x}{a} + \frac{y}{b} = 1$ .
Câu 39: Nhận biết
Chọn đáp án đúng

Xét vị trí tương đối của hai đường thẳng $\left( d_{1} ight):2x - 3y + 1 = 0$ và $\left( d_{2} ight): - 4x + 6y - 1 = 0$ ?
- A.
  Hai đường thẳng song song với nhau.
- B.
  Hai đường thẳng cắt nhau và không vuông góc với nhau.
- C.
  Hai đường thẳng trùng nhau.
- D.
  Hai đường thẳng vuông góc với nhau.
Ta có: $\frac{2}{- 4} = \frac{- 3}{6} eq \frac{1}{- 1}$

Vậy hai đường thẳng đã cho song song với nhau.
Câu 40: Nhận biết
Chọn công thức sai

Cho k, n là các số nguyên dương, k ≤ n. Trong các phát biểu sau, phát biểu nào sai?
- A.
  $A_{n}^{k}=n(n-1)...(n-k+1)$
- B.
  $P_{n}=n\times (n-1)\times (n-2)\times ...\times 2\times 1$
- C.
  $P_{n}=n!$
- D.
  $A_{n}^{k}=\frac{n!}{k!}$
Công thức sai là: $A_{n}^{k}=\frac{n!}{k!}$ .

Tải file làm trên giấy

Chia sẻ bởi:
Khang Anh

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Thời gian còn lại 90:00 Số câu đã làm 0/40

Chưa làm Đã làm

Tìm bài trong mục này

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Đấu Trường Tri Thức

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Đề thi giữa học kì 2 Toán 10 Kết nối tri thức (Đề 4)

Đổi điểm làm bài

Chúc mừng Bạn đã hoàn thành bài!