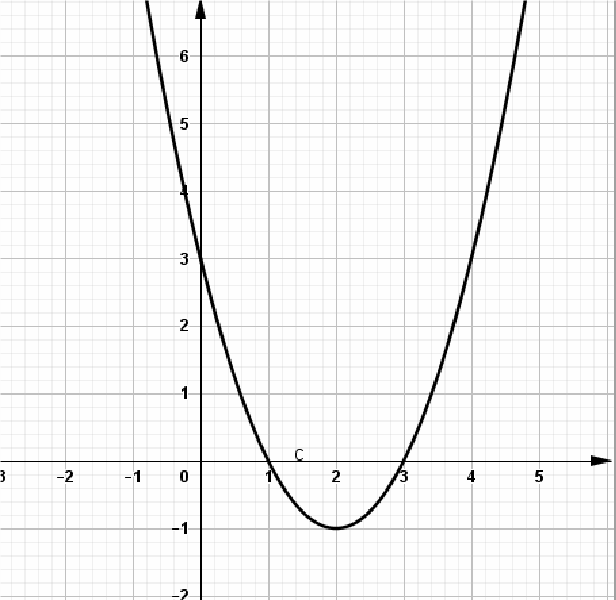
Bằng phép tịnh tiến, từ đồ thị hàm số y = − 2x2suy ra đồ thị hàm số y = − 2x2 − 6x + 3 như thế nào?
Xét
Do đó tịnh tiến đồ thị hàm số y = − 2x2 để được đồ thị hàm số y = − 2x2 − 6x + 3 ta làm như sau:
Tịnh tiến liên tiếp đồ thị hàm số y = − 2x2 đi sang bên trái đơn vị và lên trên đi
đơn vị.