Hàm số bậc hai
Bài học: Lí thuyết toán 10: Hàm số bậc hai (Kết nối tri thức) đã giới thiệu cho các em về khái niệm hàm số hàm số bậc hai, đồ thị hàm số bậc hai. Bên cạnh đó là một số ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình toán 10 Kết nối tri thức.
1. Khái niệm hàm số bậc hai
- Là hàm số có dạng
\(y=ax^2+bx+c\) với \(a\neq0\). - Tập xác định của hàm số bậc hai là \(D=\mathbb{R}\).
- Bảng biến thiên
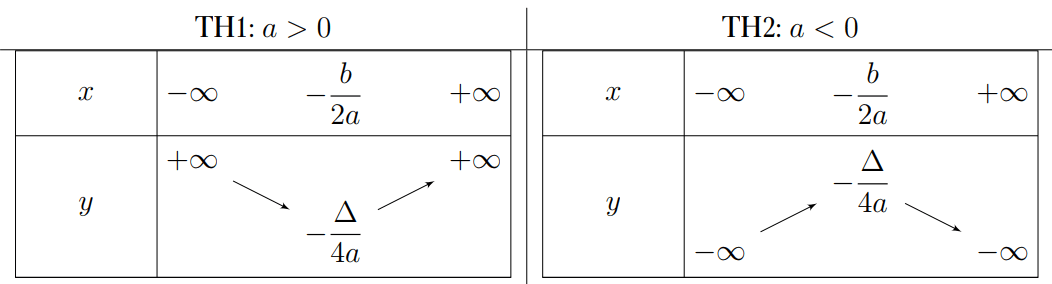
Nhận xét:
- Với \(a>0\), hàm số nghịch biến trên khoảng \(\left(-\infty;\frac{-b}{2a}\right)\) và đồng biến trên khoảng \(\left(\frac{-b}{2a};+\infty\right)\).
- Với \(a<0\), hàm số đồng biến trên khoảng \(\left(-\infty;\frac{-b}{2a}\right)\) và nghịch biến trên khoảng \(\left(\frac{-b}{2a};+\infty\right)\).
Ví dụ: Xét tính đồng biến, nghịch biến của hàm số \(y = 2{x^2} + 4x - 1\) trên \(\mathbb{R}\).
Hướng dẫn giải
Ta có: \(\frac{-b}{2a}=-1\), mà \(a=2>0\) nên hàm số nghịch biến trên khoảng \((-\infty;-1)\) và đồng biến trên khoảng \((-1;+\infty)\).
2. Đồ thị hàm số bậc hai
Đồ thị hàm số \(y=ax^2+bx+c\) \((a\neq0)\) là một parabol \((P)\) có:
- Đỉnh \(I\left( {\frac{{ - b}}{{2a}}; - \frac{\Delta }{{4a}}} \right)\).
- Trục đối xứng là đường thẳng \(x=-\frac{b}{2a}\). Đường thẳng này đi qua đỉnh \(I\) và song song với trục \(Oy\).
- Bề lõm quay lên trên khi \(a>0\) và bề lõm quay xuống dưới khi \(a<0\).
- Cắt trục tung tại điểm có tung độ bằng \(c\), tức là đồ thị luôn đi qua điểm có tọa độ \(\left ( 0;c \right )\).
Để vẽ đường parabol \(y=ax^2+bx+c\) \((a\neq0)\) ta tiến hành theo các bước như sau:
- Xác định tọa độ đỉnh \(I\left( {\frac{{ - b}}{{2a}}; - \frac{\Delta }{{4a}}} \right)\);
- Vẽ trục đối xứng \(x=-\frac{b}{2a}\);
- Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol;
- Vẽ parabol.
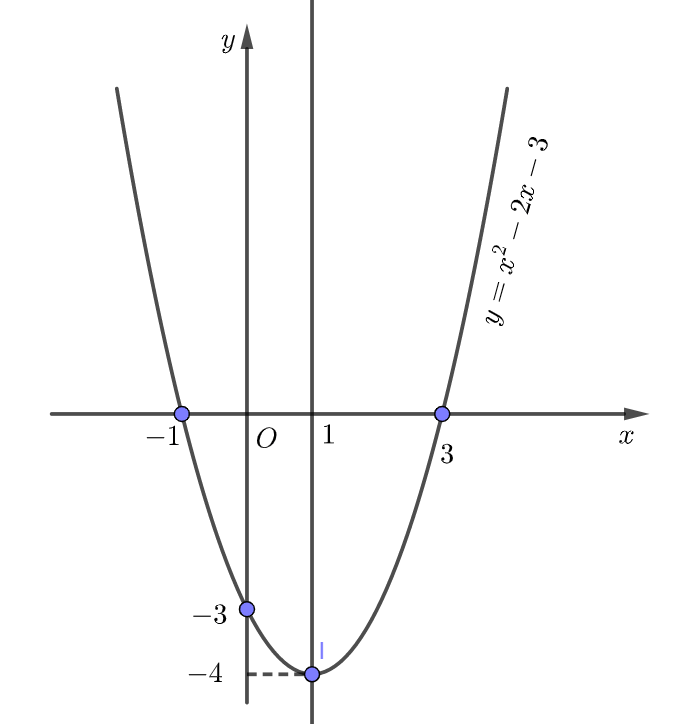
Ví dụ 1: Khảo sát và vẽ đồ thị của hàm số \(y=x^2-2x-3\).
Hướng dẫn giải
Đỉnh \(I\left(1;-4\right)\).
Trục đối xứng của hàm số: \(x=1\).
Cho \(x=0\) suy ra \(y=-3\). Suy ra giao điểm của đồ thị với trục tung là điểm \((0;-3)\).
Cho \(y=0\) để tìm giao điểm của đồ thị với trục hoành. Ta có: \(y=x^2-2x-3 =0\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = - 1}\\
{x = 3}
\end{array}} \right.\). Suy ra giao điểm của đồ thị với trục hoành là hai điểm \((-1;0)\) và \((3;0)\).
Ví dụ 2: Xác định hệ số \(a;b\) của công thức hàm số bậc hai \(y=ax^2+bx+1\). Biết đồ thị hàm số đi qua điểm \(A(1;0)\) và có trục đối xứng \(x=1\).
Hướng dẫn giải
Đồ thị hàm số đi qua điểm \(A(1;0)\) nên thay tọa độ điểm \(A\) vào công thức hàm số: \(0=a+b+1\Leftrightarrow a+b=-1\) (1).
Trục đối xứng \(x=1=-\frac{b}{2a}\Leftrightarrow 2a+b=0\) (2).
Từ (1) và (2), suy ra \(a=1\,;\,b=-2\).
