Bất phương trình bậc nhất hai ẩn
Bất phương trình bậc nhất hai ẩn ![]() \(x;y\) là bất phương trình có một trong các dạng sau:
\(x;y\) là bất phương trình có một trong các dạng sau:![]() \(ax+by \le c; ax+by < c;\)
\(ax+by \le c; ax+by < c;\) ![]() \(ax+by \ge c ; ax+by >c\). Trong đó
\(ax+by \ge c ; ax+by >c\). Trong đó ![]() \(a,b,c\) là các số cho trước;
\(a,b,c\) là các số cho trước; ![]() \(a,b\) không đồng thời bằng
\(a,b\) không đồng thời bằng ![]() \(0\) và
\(0\) và ![]() \(x,y\) là các ẩn.
\(x,y\) là các ẩn.
Ví dụ:
Các bất phương trình ![]() \(x+3y>2;2x-y\le0;\)
\(x+3y>2;2x-y\le0;\)![]() \(3y+11 \ge0\) là các bất phương trình bậc nhất hai ẩn.
\(3y+11 \ge0\) là các bất phương trình bậc nhất hai ẩn.
Bất phương trình ![]() \(9x^2+y<1\) không là bất phương trình bậc nhất hai ẩn vì chứa
\(9x^2+y<1\) không là bất phương trình bậc nhất hai ẩn vì chứa ![]() \(x^2\).
\(x^2\).
2. Nghiệm của bất phương trình bậc nhất hai ẩn
Xét bất phương trình ![]() \(ax+by < c\).
\(ax+by < c\).
- Mỗi cặp số
 \((x_0;y_0)\) thỏa mãn
\((x_0;y_0)\) thỏa mãn  \(ax_0+by_0 < c\) được gọi là một nghiệm của bất phương trình đã cho.
\(ax_0+by_0 < c\) được gọi là một nghiệm của bất phương trình đã cho. - Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.
Ví dụ: Cho bất phương trình bậc nhất hai ẩn ![]() \(2x-y>3\). Cặp số nào sau đây là một nghiệm của bất phương trình bậc nhất hai ẩn trên?
\(2x-y>3\). Cặp số nào sau đây là một nghiệm của bất phương trình bậc nhất hai ẩn trên?
a) ![]() \((x;y)=(1;2)\);
\((x;y)=(1;2)\);
b) ![]() \((x;y)=(3;1)\).
\((x;y)=(3;1)\).
Hướng dẫn giải
a) Vì ![]() \(2.1-2=0<3\) nên cặp số
\(2.1-2=0<3\) nên cặp số ![]() \((1;2)\) không là nghiệm của
\((1;2)\) không là nghiệm của ![]() \(2x-y>3\).
\(2x-y>3\).
b) Vì ![]() \(2.3-1=5>3\) nên cặp số
\(2.3-1=5>3\) nên cặp số ![]() \((1;2)\) là nghiệm của
\((1;2)\) là nghiệm của ![]() \(2x-y>3\).
\(2x-y>3\).
3. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn
- Trong mặt phẳng tọa độ
 \(Oxy\), tập hợp các điểm có tọa độ là nghiệm của bất phương trình
\(Oxy\), tập hợp các điểm có tọa độ là nghiệm của bất phương trình  \(ax+by \le c\) được gọi là miền nghiệm của bất phương trình đó.
\(ax+by \le c\) được gọi là miền nghiệm của bất phương trình đó. - Đường thẳng
 \(d\) có phương trình
\(d\) có phương trình  \(ax+by=c\) chia mặt phẳng tọa độ
\(ax+by=c\) chia mặt phẳng tọa độ  \(Oxy\) ra làm hai nửa mặt phẳng bờ
\(Oxy\) ra làm hai nửa mặt phẳng bờ  \(d\):
\(d\): - Một nửa mặt phẳng (không kể bờ
 \(d\)) gồm các điểm có tọa độ
\(d\)) gồm các điểm có tọa độ  \((x;y)\) thỏa mãn
\((x;y)\) thỏa mãn  \(ax+by>c\).
\(ax+by>c\). - Nửa mặt phẳng còn lại (không kể bờ
 \(d\)) gồm các điểm có tọa độ
\(d\)) gồm các điểm có tọa độ  \((x;y)\) thỏa mãn
\((x;y)\) thỏa mãn  \(ax + by < c\).
\(ax + by < c\). - Bờ
 \(d\) bao gồm các điểm có tọa độ
\(d\) bao gồm các điểm có tọa độ  \((x;y)\) thỏa mãn
\((x;y)\) thỏa mãn  \(ax+by=c\).
\(ax+by=c\).
Cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn ![]() \(ax+by\ge c\).
\(ax+by\ge c\).
- Vẽ đường thẳng
 \(d:ax+by=c\) trên mặt phẳng tọa độ
\(d:ax+by=c\) trên mặt phẳng tọa độ  \(Oxy\).
\(Oxy\). - Lấy 1 điểm
 \(M(x_0;y_0)\) không thuộc
\(M(x_0;y_0)\) không thuộc  \(d\).
\(d\). - Tính
 \(ax_0+by_0\) và so sánh với
\(ax_0+by_0\) và so sánh với  \(c\).
\(c\). - Nếu
 \(ax_0+by_0>c\) thì nửa mặt phẳng tính cả bờ
\(ax_0+by_0>c\) thì nửa mặt phẳng tính cả bờ  \(d\) chứa
\(d\) chứa  \(M\) là miền nghiệm của bất phương trình. Nếu
\(M\) là miền nghiệm của bất phương trình. Nếu  \(ax_0+by_0 > c\) thì nửa mặt phẳng tính cả bờ
\(ax_0+by_0 > c\) thì nửa mặt phẳng tính cả bờ  \(d\) không chứa
\(d\) không chứa  \(M\) là miền nghiệm của bất phương trình.
\(M\) là miền nghiệm của bất phương trình.
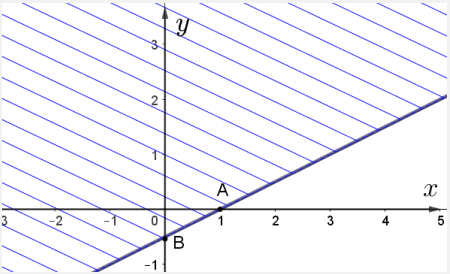
Ví dụ: Biểu diễn miền nghiệm của bất phương trình ![]() \(x-2y \ge 1\).
\(x-2y \ge 1\).
Hướng dẫn giải
Vẽ đường thẳng ![]() \(d:x-2y=1\) đi qua hai điểm
\(d:x-2y=1\) đi qua hai điểm ![]() \(A(1;0);B (0;-\frac12)\).
\(A(1;0);B (0;-\frac12)\).
Xét điểm ![]() \(O(0;0) \notin d\). Ta thấy
\(O(0;0) \notin d\). Ta thấy ![]() \(0-2.0=0<1\). Do đó miền nghiệm của bất phương trình là nửa mặt phẳng tính cả bờ
\(0-2.0=0<1\). Do đó miền nghiệm của bất phương trình là nửa mặt phẳng tính cả bờ ![]() \(d\), không chứa gốc tọa độ
\(d\), không chứa gốc tọa độ ![]() \(O\). (miền nghiệm là miền không bị gạch chéo)
\(O\). (miền nghiệm là miền không bị gạch chéo)