Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức

Mô tả thêm:

Đề kiểm tra 45 phút Toán 10 Chương 1 Mệnh đề và tập hợp sách Kết nối tri thức giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
  • Thời gian làm: 45 phút
  • Số câu hỏi: 40 câu
  • Số điểm tối đa: 40 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Vận dụng

    Chọn đáp án thích hợp

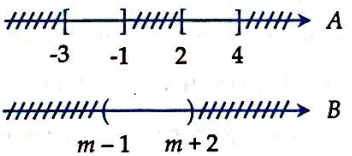
    Cho mệnh đề chứa biến P(x) = \left\{ x\mathbb{\in Z}:\left| x^{2} - 2x - 3 \right| = x^{2} + |2x + 3| \right\}. Trong đoạn \lbrack - 2020;2021\rbrack có bao nhiêu giá trị của x để mệnh đề chứa biến P(x) là mệnh đề đúng?

    Số giá trị nguyên để mệnh đề P(x) là mệnh đề đúng chính là số nghiệm nguyên của phương trình \left| x^{2} - 2x - 3 \right| = x^{2} + |2x + 3|\ \ (1)

    + Nếu x \geq - \frac{3}{2} thì ta có

    (1) \Leftrightarrow \left| x^{2} - 2x - 3 \right| = x^{2} + 2x + 3

    \Leftrightarrow \left\lbrack \begin{matrix} x^{2} - 2x - 3 = x^{2} + 2x + 3 \\ - x^{2} + 2x + 3 = x^{2} + 2x + 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} x = - \frac{3}{2} \\ x = 0 \\ \end{matrix} \right..

    + Nếu x < - \frac{3}{2} thì ta có (1) \Leftrightarrow \left| x^{2} - 2x - 3 \right| = x^{2} - 2x - 3. Sử dụng định nghĩa giá trị tuyệt đối, kết hợp với điều kiện, ta có nghiệm của (1) trong trường hợp này:

    (1) \Leftrightarrow \left\{ \begin{matrix} x^{2} - 2x - 3 \geq 0 \\ x < - \frac{3}{2} \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} x \leq - 1 \\ x \geq 3 \\ \end{matrix} \right.\ \\ x < - \frac{3}{2} \\ \end{matrix} \right.\ \Leftrightarrow x < - \frac{3}{2}

    Phương trình đã cho có tập nghiệm nguyên trên đoạn \lbrack - 2020;2021\rbrack là S = \left\{ 0; - 2; - 3;...; - 2020 \right\}.

    Vậy có 2020 số nguyên thỏa mãn yêu cầu bài toán.

  • Câu 2: Nhận biết

    Chọn đáp án thích hợp

    Khẳng định nào sau đây là mệnh đề?

    Đáp án cần tìm là: “Sao hỏa không thuộc hệ thái dương”.

  • Câu 3: Thông hiểu

    Tìm mệnh đề sai trong các mệnh đề sau

    Cho 2 mệnh đề: “Quyển vở này của Nam” và “Quyển vở này có 118 trang”.

    Cho biết 2 mệnh đề trên đều đúng, tìm mệnh đề sai trong các mệnh đề sau:

    Đặt P: “Quyển vở này của Nam”, Q: “Quyển vở này có 118 trang”

    Theo đề bài, P đúng, Q đúng nên \overline{P} sai, \overline{Q} sai.

    Mệnh đề P \Rightarrow Q chỉ sai khi P đúng Q sai.

    Chọn đáp án Quyển vở này của Nam nên nó không có 118 trang.

  • Câu 4: Thông hiểu

    Xác định tập hợp X thỏa mãn điều kiện

    Cho hai tập hợp A = \left\{ 0;2 \right\} và B = \left\{ 0;1;2;3;4 \right\}.Có bao nhiêu tập hợp X thỏa mãn A \cup X = B.

    Liệt kê các tập hợp X thỏa \left\{ 1;3;4 \right\},\left\{ 0;1;3;4\right\},\left\{ 1;2;3;4 \right\},\left\{ 0;1;2;3;4\right\}.

    Do đó chọn đáp án 4.

  • Câu 5: Thông hiểu

    Tìm mệnh đề đảo đúng

    Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

    Câu đúng là: “Nếu số nguyên n có chữ số tận cùng là 0 thì số nguyên n chia hết cho 5”.

  • Câu 6: Nhận biết

    Xác định mệnh đề đúng

    Trong các câu sau, câu nào là một mệnh đề đúng?

    Ta có: \sqrt{9} = 3 nên “\sqrt{9} \geq 3” là một mệnh đề đúng.

  • Câu 7: Nhận biết

    Tìm khẳng định đúng

    Khẳng định nào đúng trong các khẳng định sau:

    Khẳng định đúng: "Nếu A ⊂ B và B ⊂ C thì A ⊂ C" 

  • Câu 8: Thông hiểu

    Chọn kết luận đúng

    Cho các tập hợp A = \left\{ x\mathbb{\in R}|\ x < 3 \right\}, B = \left\{ x\mathbb{\in R}|1 < x \leq 5 \right\}, C = \left\{ x\mathbb{\in R}| - 2 \leq x \leq 4 \right\}. Khi đó (B \cup C)\backslash(A \cap C) bằng

    Ta có:

    A = ( - \infty;\ 3), B = (1;\ 5\rbrack, C = \lbrack - 2;\ 4\rbrack.

    Khi đó:

    (B \cup C)\backslash(A \cap C)

    = \left\{ (1;\ 5\rbrack \cup \lbrack - 2;\ 4\rbrack \right\}\backslash\left\{ ( - \infty;\ 3) \cap \lbrack - 2;4\rbrack \right\}

    = \lbrack - 2;5\rbrack\backslash\lbrack - 2;\ 3) = \lbrack 3;\ 5\rbrack.

  • Câu 9: Thông hiểu

    Tìm câu sai

    Mệnh đề nào sau là mệnh đề sai?

    Ta có 0\mathbb{\in R} và 0^{2} = 0 nên mệnh đề \forall x\mathbb{\in R}:x^{2} > 0 là mệnh đề sai.

     

  • Câu 10: Nhận biết

    Chọn đáp án đúng

    Kết quả của phép toán ( - \infty;\ 1) \cap \lbrack - 1;\ 2) là

    Ta có ( - \infty;\ 1) \cap \lbrack - 1;\ 2) = \lbrack - 1;\ \ 1).

  • Câu 11: Nhận biết

    Tìm phần bù của phép toán

    Xác định phần bù của tập hợp ( - \infty\ ;\ - 2) trong ( - \infty\ ;\ 4).

    Ta có: C_{( - \infty\ ;\ 4)}( - \infty\ ;\ - 2) = ( - \infty\ ;\ 4)\backslash( - \infty\ ;\ - 2) = \lbrack - 2\ ;\ 4).

  • Câu 12: Thông hiểu

    Chọn đáp án đúng

    Cho số thực a < 0. Điều kiện cần và đủ để ( - \infty;9a) \cap \left( \frac{4}{a}; + \infty \right) \neq \varnothing là

    Ta có:

    ( - \infty;9a) \cap \left( \frac{4}{a}; + \infty \right) \neq \varnothing

    \Leftrightarrow 9a > \frac{4}{a} \Leftrightarrow \left\lbrack \begin{matrix} a > \frac{2}{3} \\ - \frac{2}{3} < a < 0 \\ \end{matrix} \right..

    Vì a < 0 nên giá trị của a cần tìm là - \frac{2}{3} < a < 0.

  • Câu 13: Nhận biết

    Chọn phương án thích hợp

    Trong các câu sau đây, câu nào là mệnh đề?

    Vì đáp án C là một câu khẳng định đúng.

  • Câu 14: Nhận biết

    Tìm mệnh đề phủ định mệnh đề đã cho

    Cho mệnh đề: “Có một học sinh trong lớp 10A không thích học môn Toán”. Mệnh đề phủ định của mệnh đề này là:

    Mệnh đề phủ định của mệnh đề “Có một học sinh trong lớp 10A không thích học môn Toán”” là “Mọi học sinh trong lớp 10A đều thích học môn Toán”

  • Câu 15: Thông hiểu

    Chọn kết quả đúng

    Cho các tập A = \left\{ x\mathbb{\in R}|x \geq - 1 \right\}, B = \left\{ x\mathbb{\in R}|x < 3 \right\}. Tập \mathbb{R}\backslash(A \cap B) là :

    Ta có : A = \lbrack - 1; + \infty) ; B = ( - \infty;3).

    Khi đó A \cap B = \lbrack - 1;3)\mathbb{\Rightarrow R}\backslash(A \cap B) = ( - \infty; - 1) \cup \lbrack 3; + \infty).

  • Câu 16: Thông hiểu

    Xác định mệnh đề phủ định

    Phủ định của mệnh đề "\exists x \in Q:2x^{2} - 5x + 2 = 0"là

    Phủ định của mệnh đề "\exists x \in Q:2x^{2} - 5x + 2 = 0" là: "\forall x \in Q:2x^{2} - 5x + 2 \neq 0".

  • Câu 17: Nhận biết

    Chọn khẳng định đúng

    Cho hai tập hợp A = \left\{ x\mathbb{\in R}| - 3 < x \leq 2 \right\}, B = ( - 1;\ 3). Chọn khẳng định đúng trong các khẳng định sau:

    Ta có:

    A = \left\{ x\mathbb{\in R}| - 3 < x \leq 2 \right\} = ( - 3;\ 2\rbrack

    \Rightarrow ( - 3;\ 2\rbrack \cap ( - 1;\ 3) = ( - 1;\ 2\rbrack.

  • Câu 18: Nhận biết

    Tìm mệnh đề đảo

    Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?

    Đáp án cần tìm là: “Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong”.

  • Câu 19: Thông hiểu

    Chọn mệnh đề đúng

    Trong các mệnh đề sau, mệnh đề nào đúng?

    Mệnh đề “\exists n\mathbb{\in N},n(n + 1)(n + 2) là số lẻ”. sai vì số tự nhiên liên tiếp n,n + 1,n + 2 luôn có ít nhất 1 số chẵn nên tích của chúng là số chẵn.

    Mệnh đề “\forall x\mathbb{\in R},x^{2} < 4 \Leftrightarrow - 2 < x < 2” đúng vì x^{2} < 4 \Leftrightarrow |x| < 2 \Leftrightarrow - 2 < x < 2.

    Mệnh đề “\exists n\mathbb{\in N},n^{2} + 1 chia hết cho 3” sai vì n^{2} luôn chia hết cho 3 hoặc chia 3 dư 1 nên n^{2} + 1 hoặc chia 3 dư 1 hoặc chia 3 dư 2 hay n^{2} + 1 không chia hết cho 3 với mọi n\mathbb{\in N}.

    Mệnh đề “\forall x\mathbb{\in R},x^{2} \geq 9 \Leftrightarrow x \geq \pm 3” sai vì x^{2} \geq 9 \Leftrightarrow |x| \geq 3 \Leftrightarrow \left\lbrack \begin{matrix} x \geq 3 \\ x \leq - 3 \\ \end{matrix} \right..

  • Câu 20: Thông hiểu

    Tập X có bao nhiêu tập con?

    Tập X có bao nhiêu tập hợp con, biết X có 3 phần tử ?

    Tập X có 3 phần tử \Rightarrow số tập con của X bằng: 2^{3} = 8.

  • Câu 21: Nhận biết

    Tìm số tập con của tập A

    Cho tập hợp A = \left\{ a,\ b,\ c,\ d \right\}. Tập A có mấy tập con?

    Số tập hợp con của tập hợp có 4 phần tử là 2^{4} = 16 tập hợp con.

  • Câu 22: Vận dụng

    Xác định tham số a theo yêu cầu

    Cho hai tập A = \lbrack 0;5\rbrack; B = (2a;3a + 1\rbrack, a > - 1. Với giá trị nào của a thì A \cap B \neq \varnothing.

    Trước hết tìm a để A \cap B = \varnothing. Với a > - 1 \Rightarrow 2a < 3a + 1.

    Ta có A \cap B = \varnothing \Leftrightarrow \left\lbrack \begin{matrix} 5 \leq 2a \\ 3a + 1 < 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} a \geq \frac{5}{2} \\ a < - \frac{1}{3} \\ \end{matrix} \right..

    Từ đó, kết hợp điều kiện ta có A \cap B \neq \varnothing \Leftrightarrow \left\lbrack \begin{matrix} a < \frac{5}{2} \\ a \geq - \frac{1}{3} \\ \end{matrix} \right..

  • Câu 23: Nhận biết

    Cách viết tập hợp nào đúng

    Cách viết tập hợp nào đúng trong các cách viết sau để xác định tập hợp A các ước dương của 12:

    Các ước dương của 12 là: 1; 2; 3; 4; 6; 12

    => Cách viết tập hợp đúng là: A = \left \{ 1; 2; 3; 4; 6; 12ight \}

  • Câu 24: Thông hiểu

    Liệt kê các phần tử của tập X

    Hãy liệt kê các phần tử của tập X =\left\{ x\mathbb{\in Z}\left| x^{4} - 6x^{2} + 8 = 0 \right.\ \right\}.

    Ta có x^{4} - 6x^{2} + 8 = 0 \Leftrightarrow \left\{ \begin{matrix} x^{2} = 4 \\ x^{2} = 2 \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} x = \pm 2\mathbb{\in Z} \\ x = \pm \sqrt{2}\mathbb{\notin Z} \\ \end{matrix} \right. nên X = \left\{ - 2;2 \right\}.

  • Câu 25: Thông hiểu

    Chọn mệnh đề đúng

    Cho P là mệnh đề đúng, Q là mệnh đề sai, chọn mệnh đề đúng trong các mệnh đề sau.

     P là mệnh đề đúng, Q là mệnh đề sai nên mệnh đề P \Rightarrow Q là mệnh đề sai, do đó \overline{P \Rightarrow Q} là mệnh đề đúng.

  • Câu 26: Nhận biết

    Tìm phát biểu mệnh đề

    Tìm phát biểu là mệnh đề.

    Ta có:

    Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai.

    Suy ra “Hà Nội là thủ đô của Việt Nam.” là mệnh đề.

  • Câu 27: Thông hiểu

    Có bao nhiêu mệnh đề trong các câu sau?

    Có bao nhiêu mệnh đề trong các câu sau?

    Số nguyên dương là số tự nhiên khác 0.

    Bạn hãy cố gắng, nhất định bạn sẽ thành công.

    Tổng các góc của một tam giác là 180{^\circ}.

    Cố lên, sắp đến nơi rồi!

    Câu “Số nguyên dương là số tự nhiên khác 0.” và “Tổng các góc của một tam giác là 180{^\circ}.” là mệnh đề.

  • Câu 28: Vận dụng

    Trong các mệnh đề sau, mệnh đề nào sai?

    Trong các mệnh đề sau, mệnh đề nào sai?

    Với n = 1\mathbb{\in N} ta có: 1^{2} > 1 là mệnh đề sai

    \Rightarrow Mệnh đề n"" alt=""\forall n\mathbb{\in N},n^{2} > n"" /> là mệnh đề sai.

  • Câu 29: Thông hiểu

    Chọn phương án thích hợp

    Sử dụng thuật ngữ “điều kiện cần” để phát biểu định lý “Với mọi số tự nhiên chia hết cho 5thì n^{2} - 1 và n^{2} + 1 đều không chia hết cho 5”

    Với mọi số tự nhiên n, điều kiện cần để nchia hết cho 5 là n^{2} - 1 và n^{2} + 1 đều không chia hết cho 5.

  • Câu 30: Thông hiểu

    Tìm mệnh đề đúng

    Cho các tập hợp M = \{ x\mathbb{\in N}\left| x \right. là bội của 2\}, N = \{ x\mathbb{\in N}\left| x \right. là bội của 6\}, P = \{ x\mathbb{\in N}\left| x \right. là ước của 2\}, Q = \{ x\mathbb{\in N}\left| x \right. là ước của 6\}. Mệnh đề nào sau đây đúng?

    Ta có các tập hợp \left\{ \begin{matrix} M = \left\{ x\left| x = 2k,\ \ k \in \mathbb{N}^{*} \right.\ \right\} = \left\{ 2;4;6;8;10;... \right\} \\ N = \left\{ x\left| x = 6k,\ \ k \in \mathbb{N}^{*} \right.\ \right\} = \left\{ 6;12;18;24;... \right\} \\ P = \left\{ 1;2 \right\} \\ Q = \left\{ 1;2;3;6 \right\} \\ \end{matrix} \right..

    Do đó P \cap Q = Q.

  • Câu 31: Nhận biết

    Chọn phương án thích hợp

    Phủ định của mệnh đề: “Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

    Phủ định của “có ít nhất” là “mọi”

    Phủ định của “tuần hoàn” là “không tuần hoàn”.

    Vậy đáp án cần tìm là: “Mọi số vô tỉ đều là số thập phân vô hạn không tuần hoàn”.

  • Câu 32: Thông hiểu

    Chọn đáp án đúng

    Cho hai tập hợp A = \left\{ x\mathbb{\in Z}\left| (x^{2} - 10x + 21)(x^{3} - x) = 0 \right.\ \right\}, B = \left\{ x\mathbb{\in Z}\left| - 3 < 2x + 1 < 5 \right.\ \right\} khi đó tập X = A \cup B là:

    Cách 1: Giải phương trình \left\lbrack \begin{matrix} x^{2} - 10x + 21 = 0 \\ x^{3} - x = 0 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} \left\lbrack \begin{matrix} x = 3 \\ x = 7 \\ \end{matrix} \right.\ \\ \left\lbrack \begin{matrix} x = 0 \\ x = \pm 1 \\ \end{matrix} \right.\ \\ \end{matrix} \right..

    Mà x\mathbb{\in Z} nên A = \left\{ - 1;0;1;3;7 \right\}

    Giải bất phương trình - 3 < 2x + 1 < 5 \Leftrightarrow - 2 < x < 2. mà x\mathbb{\in Z} nên chọn B = \left\{ - 1;0;1 \right\}

    Giải bất phương trình A \cup B = \left\{ - 1;0;1;3;7 \right\}

    Cách 2: Ta thử từng phần tử của các đáp án, nếu thỏa yêu cầu bài toán của cả tập A hoặc B thì đó là đáp án đúng.

  • Câu 33: Nhận biết

    Hãy liệt kê các phần tử của tập hợp

    Cho tập hợp A = {x\mathbb{\in N}\left| x \right. là ước chung của 36 và 120}. Hãy liệt kê các phần tử của tập hợp A.

    Ta có \left\{ \begin{matrix} 36 = 2^{2}.3^{2} \\ 120 = 2^{3}.3.5 \\ \end{matrix} \right.. Do đó A = \left\{ 1;2;3;4;6;12 \right\}.

  • Câu 34: Nhận biết

    Chọn câu đúng

    Cho A = ( - 5;1\rbrack, B = \lbrack 3; + \infty), C = ( - \infty; - 2). Câu nào sau đây đúng?

    Đáp án đúng là: “B \cap C = \phi”.

  • Câu 35: Nhận biết

    Chọn đáp án đúng

    Mệnh đề nào sau đây là mệnh đề tương đương?

    Mệnh đề tương đương là: “Hình thang nội tiếp đường tròn khi và chỉ khi nó là hình thang cân”.

  • Câu 36: Vận dụng cao

    Tìm tập hợp tham số m

    Cho tập hợp khác rỗng \left\lbrack m - 1;\frac{m + 3}{2} ightbrack và B = ( - \infty - 3) \cup \lbrack 3; + \infty). Tập hợp các giá trị thực của tham số m để A \cap B eq \varnothing

    Để A \cap B eq \varnothing thì điều kiện là: \left\{ \begin{gathered} m - 1 < \dfrac{{m + 3}}{2} \hfill \\ \left[ {\begin{array}{*{20}{c}} {m - 1 < - 3} \\ {\dfrac{{m + 3}}{2} \geqslant 3} \end{array}} ight. \hfill \\ \end{gathered} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {m < 5} \\ {\left[ {\begin{array}{*{20}{c}} {m < - 2} \\ {m \geqslant 3} \end{array}} ight.} \end{array}} ight.

    Vậy m \in ( - \infty; - 2) \cup \lbrack 3;5) thỏa mãn điều kiện.

  • Câu 37: Thông hiểu

    Phủ định mệnh đề A

    Cho mệnh đề 0" thì phủ định của A là:

    Ta có phủ định của mệnh đề A là:  \overline{A}:\ "\exists x\mathbb{\in R}:x^{2} + 2x + 1 \leq 0".

  • Câu 38: Nhận biết

    Kí hiệu mệnh đề kéo theo

    Đâu là kí hiệu của hai mệnh đề kéo theo?

    Mệnh đề kéo theo được kí hiệu là: P ⇒ Q

  • Câu 39: Nhận biết

    Chọn phương án thích hợp

    Cho A, B là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?

    Theo biểu đồ Ven thì phần gạch sọc trong hình vẽ là tập hợp A \cap B.

  • Câu 40: Vận dụng cao

    Tìm tham số m thỏa mãn điều kiện

    Cho hai tập hợp A = \lbrack - 3; - 1\rbrack \cup \lbrack 2;4\rbrack, B = (m - 1;m + 2). Tìm m để A \cap B \neq \varnothing.

    Biểu diễn tập hợp trên trục số

    Ta đi tìm m để A \cap B = \varnothing

    \Rightarrow \left\lbrack \begin{matrix} m + 2 \leq - 3 \\ m - 1 \geq 4 \\ \left\{ \begin{matrix} - 1 \leq m - 1 \\ m + 2 \leq 2 \\ \end{matrix} \right.\ \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} m \leq - 5 \\ m \geq 5 \\ m = 0 \\ \end{matrix} \right.

    \Rightarrow A \cap B \neq \varnothing \Leftrightarrow \left\{ \begin{matrix} - 5 < m < 5 \\ m \neq 0 \\ \end{matrix} \right.

    hay \left\{ \begin{matrix} |m| < 5 \\ m \neq 0 \\ \end{matrix} \right.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Làm lại
1
41 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề kiểm tra 45 phút Đại số 10 Chương 1 Kết nối tri thức
Thời gian còn lại 45:00 Số câu đã làm 0/40
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 10 - Kết nối tri thức
Xem thêm