Hệ thức lượng trong tam giác
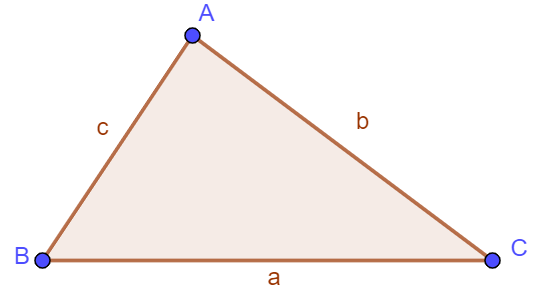
Cho tam giác 
\(ABC\) có \(AB=c,BC=a,CA=b\), ta có:
- \(a^2=b^2+c^2-2bc\cos A\);
- \(b^2=a^2+c^2-2ac\cos B\);
- \(c^2=a^2+b^2-2ab\cos C\).
Hệ quả
- \(\cos A=\frac{b^2+c^2-a^2}{2bc}\);
- \(\cos B=\frac{a^2+c^2-b^2}{2ac}\);
- \(\cos C=\frac{a^2+b^2-c^2}{2ab}\).
Ví dụ 1: Cho tam giác \(ABC\) có \(\hat{A} =120^{\circ}\) và \(AB=3,AC=4\). Tinh độ dài cạnh \(BC\).
Hướng dẫn giải
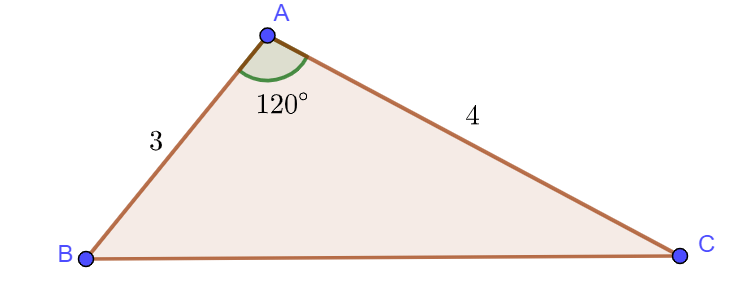
Áp dụng định lý côsin cho tam giác \(ABC\), ta có:
\(BC^2=AB^2+AC^2-2AB.AC.\cos A\)\(=3^2+4^2-2.3.4.\cos 60^{\circ} =13\).
Suy ra \(BC=\sqrt{13}\).
Ví dụ 2: Cho tam giác \(ABC\) có \(a=19,b=6,c=15\). Tính giá trị góc \(\hat A\). (kết quả làm tròn đến hàng phần trăm)
Hướng dẫn giải
Áp dụng hệ quả của định lý côsin cho tam giác \(ABC\), ta có:
\(\cos A= \frac{b^2+c^2-a^2}{2bc}\)\(=\frac{6^2+15^2-19^2}{2.6.15}=-\frac59\).
Suy ra \(\hat A\approx 123,75^{\circ}\).
2. Định lý sin trong tam giác
Cho tam giác \(ABC\) có \(AB=c,BC=a,CA=b\) và \(R\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\), ta có:
\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)
Ví dụ: Cho tam giác \(ABC\) có \(\hat A=120^{\circ} ,\hat C=45^{\circ} ,b=6\). Tính số đo góc \(\hat B\), độ dài \(a,c,R\). (kết quả làm tròn đến hàng phần trăm)
Hướng dẫn giải
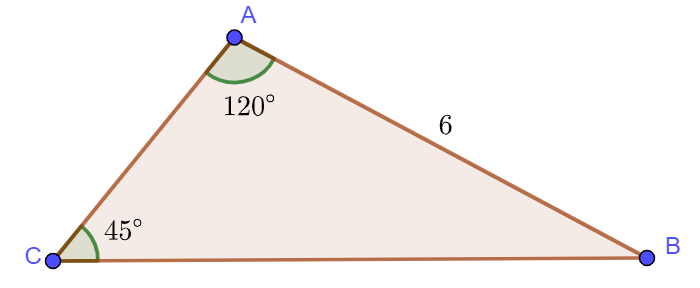
Ta có: \(\hat B=180^{\circ} -(\hat A+\hat C)\)\(=180^{\circ}-(120^{\circ} +45^{\circ} )=15^{\circ}\).
Áp dụng định lý sin trong tam giác \(ABC\): \(\frac{a}{\sin 120^{\circ} }=\frac 6{\sin 15^{\circ}}=\frac c{\sin45^{\circ}}=2R\).
Suy ra: \(a=\sin 120^{\circ} .\frac 6{\sin 15^{\circ} } \approx 20,08\), \(c=\sin 45^{\circ} .\frac 6{\sin 15^{\circ} } \approx 16,39\),\(R=\frac 6{2\sin 15^{\circ} }\approx 11,59\).
3. Các công thức tính diện tam giác
Cho tam giác \(ABC\), ta kí hiệu:
- \(AB=c,BC=a,CA=b\);
- \(h_a,h_b,h_c\) lần lượt là độ dài các đường cao kẻ từ \(A,B,C\);
- \(R\) là bán kính đường tròn ngoại tiếp;
- \(r\) là bán kính đường tròn nội tiếp;
- \(p= \frac{a+b+c}2\) là nửa chu vi;
- \(S\) là diện tích tam giác \(ABC\).
Ta có các công thức tính diện tích tam giác sau:
- \(S_{ABC}=\frac12 a.h_a=\frac12 b.h_b =\frac12 c.h_c\);
- \(S_{ABC}=\frac12bc\sin A=\frac12ac\sin B=\frac12ab\sin C\);
- \(S_{ABC}=\frac {abc}{4R}\);
- \(S_{ABC}=p.r\);
- \(S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}\) (Công thức Heron).
Ví dụ 1: Cho tam giác \(ABC\) có \(a=5,b=6,c=7\). Tính diện tích tam giác \(ABC\).
Hướng dẫn giải
(Khi biết 3 cạnh của tam giác, ta sử dụng công thức Heron)
Ta có: \(p=\frac{a+b+c}2=\frac{5+6+7}2=9\).
Áp dụng công thức Heron:
\(S_{ABC}=\sqrt{p(p-a)(p-b))p-c)}\)\(=\sqrt{9(9-5)(9-6)(9-7)} = 6\sqrt6\).
Ví dụ 2: Cho tam giác \(ABC\) có \(c=3,b=4,\hat A=120^{\circ}\). Tính diện tích tam giác này.
Hướng dẫn giải
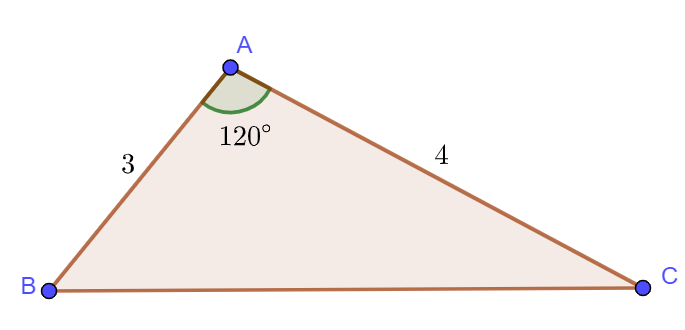
(Khi biết 2 cạnh và 1 góc xen giữa, ta sử dụng công thức số 2)
Ta có: \(S_{ABC}=\frac12bc\sin A=\frac12.3.4\sin 120^{\circ} =3\sqrt3\).
4. Giải tam giác
Giải tam giác là đi tìm số đo tất cả các cạnh và tất cả các góc của tam giác.
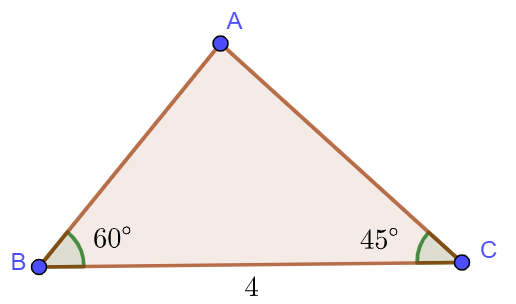
Ví dụ: Giải tam giác \(ABC\) biết \(a=4,\hat B=60^{\circ} ,\hat C=45^{\circ}\).
Hướng dẫn giải
Ta có: \(\hat A=180^{\circ} -(\hat B+\hat C)\)\(=180^{\circ} -(60^{\circ} +45^{\circ} )=75^{\circ}\).
Áp dụng định lý sin, ta có: \(\frac{4}{\sin 75^{\circ} }=\frac b{\sin 60^{\circ}}=\frac c{\sin45^{\circ}}=2R\).
Suy ra: \(b=\sin 60^{\circ} .\frac 4{\sin 75^{\circ} } \approx 3,59\), \(x=\sin 45^{\circ} .\frac 4{\sin 75^{\circ} } \approx =2,93\), \(R=\frac 4{2\sin 75^{\circ} } \approx 2,07\).
