Phương trình có bao nhiêu nghiệm
Phương trình có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?
Điều kiện: .
Ta có: .
Loại . Do đó phương trình có 1 nghiệm.
Đề kiểm tra 45 phút Toán 10 Chương 6 Hàm số, Đồ thị và ứng dụng sách Kết nối tri thức giúp bạn học tổng hợp lại kiến thức của cả nội dung chương. Cùng nhau luyện tập nha!
Phương trình có bao nhiêu nghiệm
Phương trình có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?
Điều kiện: .
Ta có: .
Loại . Do đó phương trình có 1 nghiệm.
Tìm số giá trị của m thỏa mãn điều kiện
Đường thẳng d : y = (m−3)x − 2m + 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là
A = d ∩ Ox nên tọa độ A là nghiệm của hệ:
nên
.
B = d ∩ Oy nên tọa độ B là nghiệm của hệ:
nên B(0;−2m+1).
Ta có
.
Nhận xét: Với thì A ≡ B ≡ O(0; 0) nên không thỏa mãn.
Vậy m = 4, m = 2.
Tìm m để phương trình có nghiệm
Tập tất cả các giá trị của tham số m để phương trình ![]() có nghiệm thực là
có nghiệm thực là
* Với m < 2 ⇒ phương trình vô nghiệm
* Với m ≥ 2,
.
Phương trình có nghiệm Δ′ = 2(m−1)2 + 1 > 0 đúng mọi m.
Vậy m ≥ 2 là những giá trị cần tìm hay m thuộc [2; + ∞).
Tính giá trị của hàm số tại điểm
Cho hàm số ![y=\left\{\begin{matrix}\frac{2}{x-1},x\in (-∞;0) \\ \sqrt{x+1},x\in [0;2]\\ x^{2}-1,x\in (2;5]\end{matrix}ight.](/data/image/holder.png) . Tính f(4), ta được kết quả:
. Tính f(4), ta được kết quả:
Với , ta có:
.
Tìm m để hàm số xác định
Tìm m để hàm số ![]() xác định trên khoảng (0;1).
xác định trên khoảng (0;1).
*Gọi D là tập xác định của hàm số .
*.
*Hàm số xác định trên khoảng (0;1)
.
Xác định tập nghiệm bất phương trình
Tập nghiệm của bất phương trình ![]() là?
là?
Ta có
Bảng xét dấu:
Dựa vào bảng xét dấu .
Tính giá trị của S
Biết rằng (P) : y = ax2 − 4x + c có hoành độ đỉnh bằng − 3 và đi qua điểm M(−2;1). Tính tổng S = a + c.
Vì (P) có hoành độ đỉnh bằng − 3 và đi qua M(−2;1) nên ta có hệ
Tam thức bậc hai âm khi và chỉ khi
Tam thức bậc hai f(x) = 4x2 − 12x + 9 nhận giá trị âm khi và chỉ khi
Chọn Ta có:

Dựa vào bảng xét dấu thì ta thấy không có giá trị x nào để f(x) < 0.
Tìm số các giá trị nguyên của m
Cho hàm số ![]() . Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên ℝ?
. Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên ℝ?
Hàm số có dạng y = ax + b, nên để hàm số đồng biến trên ℝ khi và chỉ khi
. Mặt khác do m ∈ ℤ nên m ∈ {−1; 0; 1; 2}. Vậy có 4 giá trị nguyên của m.
Tìm hàm số bậc hai thỏa mãn
Xác định parabol ![]() biết rằng Parabol đi qua hai điểm M(1;5) và N(-2;8)
biết rằng Parabol đi qua hai điểm M(1;5) và N(-2;8)
Thay tọa độ và
vào
. Ta có:
.
Do đó .
Đồ thị của hàm số bậc hai
Bề lõm của parabol quay lên trên đối với đồ thị hàm số bậc hai nào sau đây?
Đồ thị hàm số bậc hai là một đường parabol có đỉnh là điểm
, có trục đối xứng là đường thẳng
. Parabol này quay bề lõm lên trên nếu
.
Hàm số có
=> Đồ thị hàm số có bề lõm quay lên.
Tìm m thỏa mãn điều kiện
Tam thức f(x) = 3x2 + 2(2m−1)x + m + 4 dương với mọi x khi:
.
Tìm tọa độ đỉnh parabol
Tìm tọa độ đỉnh S của parabol: ![]() ?
?
Gọi tọa độ đỉnh của parabol là điểm
Hàm số bậc hai có:
=>
Tổng các nghiệm của phương tình bằng
Tổng các nghiệm của phương trình ![]() bằng:
bằng:
.
Vậy, tổng các nghiệm của phương trình là .
Tìm hàm số bậc hai thỏa mãn
Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?
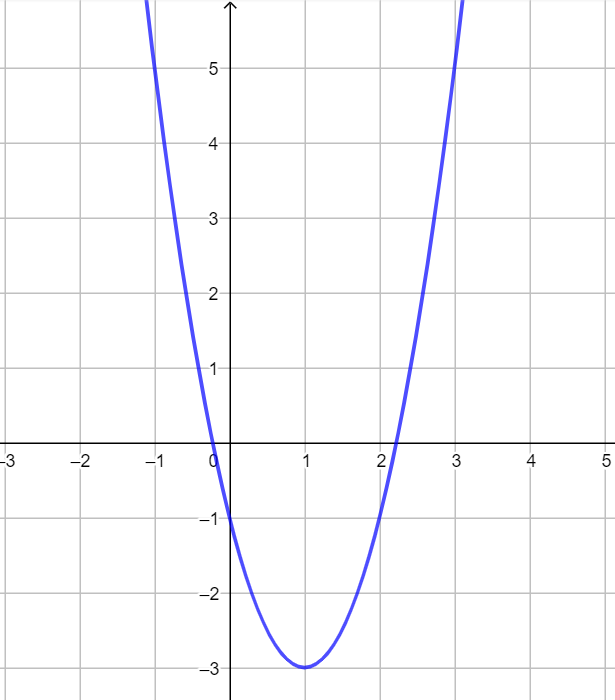
Nhận xét: Đồ thị có đỉnh .
Thay tọa độ vào hàm số
ta thấy thỏa mãn.
Giải phương trình
Nghiệm của phương trình ![]() là
là
Điều kiện:
Phương trình tương đương
Kết hợp với điều kiện ra được thỏa mãn
Vậy nghiệm của phương trình là:
Tìm hàm số thỏa mãn điều kiện
Hàm số nào sau đây nghịch biến trên khoảng (−1;+∞)?
Xét đáp án , ta có
nên
và có a < 0 nên hàm số đồng biến trên khoảng (−∞;−1) và nghịch biến trên khoảng (−1;+∞).
Tìm m thỏa mãn điều kiện
Cho f(x) = − 2x2 + (m+2)x + m − 4. Tìm m để f(x) âm với mọi a, b, c > 0.
Ta có .
Tìm x
Cho hàm số: ![]() . Tìm x để
. Tìm x để ![]()
Ta có:
Vậy x = 3 hoặc x = 0
Tìm tập nghiệm của bất phương trình
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
Số nghiệm của phương trình là
Số nghiệm của phương trình ![]() là bao nhiêu?
là bao nhiêu?
.
Vậy phương trình có hai nghiệm.
Tìm tam thức bậc hai thỏa mãn
Tam thức nào sau đây nhận giá trị âm với x < 2
Bảng xét dấu của − x2 + 5x − 6

Phương trình sau có bao nhiêu nghiệm
Phương trình sau có bao nhiêu nghiệm ![]() ?
?
Điều kiện xác định: .
Với thay vào phương trình thỏa mãn. Vậy phương trình có một nghiệm.
Chọn khẳng định sia
Cho hàm số y = − x2 + 4x + 1. Khẳng định nào sau đây sai?
Hàm số y = ax2 + bx + c với a < 0 nghịch biến trên khoảng , đồng biến trên khoảng
.
Áp dụng: Ta có Do đó hàm số nghịch biến trên khoảng (2;+∞) và đồng biến trên khoảng (−∞;2). Do đó Hàm số nghịch biến trên khoảng (4;+∞) và đồng biến trên khoảng (−∞;4) sai. Chọn đáp án này.
Đáp án Trên khoảng (−∞;−1) hàm số đồng biến đúng vì hàm số đồng biến trên khoảng (−∞;2) thì đồng biến trên khoảng con (−∞;−1).
Đáp án Trên khoảng (3;+∞) hàm số nghịch biến đúng vì hàm số nghịch biến trên khoảng (2;+∞) thì nghịch biến trên khoảng con (3;+∞).
Tập nào không là tập con của A
Gọi S là tập nghiệm của bất phương trình ![]() . Trong các tập hợp sau, tập nào không là tập con của S?
. Trong các tập hợp sau, tập nào không là tập con của S?
Tam thức bậc hai có hai nghiệm phân biệt là:
Vì a = 1 > 0 nên khi
.
Tập không phải tập con của S là:
Tính giá trị T
Gọi S là tập hợp các giá trị thực của tham số m sao cho parabol (P) : y = x2 − 4x + m cắt Ox tại hai điểm phân biệt A, B thỏa mãn OA = 3OB. Tính tổng T các phần tử của S.
Phương trình hoành độ giao điểm: x2 − 4x + m = 0. (*)
Để (P) cắt Ox tại hai điểm phân biệt A, B thì (*) có hai nghiệm phân biệt ⇔ Δ = 4 − m > 0 ⇔ m < 4.
Theo giả thiết
TH1:
TH2: : không thỏa mãn (*).
Do đó (P) Chọn A.
Tìm đồ thị hàm số phù hợp
Đồ thị của hàm số ![]() là
là
Từ giả thiết hàm số đồng biến nên loại đáp án có đồ thị đi xuống từ trái sang phải.
Mặt khác cho x = 0 vào nên chọn đáp án đồ thị hàm số đi qua điểm
.
Tìm miền giá trị của hàm số
Miền giá trị của hàm số ![]() là
là
Cách 1: Do x2 + 1 > 0; ∀x ∈ ℝ nên hàm số xác định với mọi x ∈ ℝ
Gọi y0 là giá trị tùy ý, ta có phương trình:
⇔ (3−y0)x2 + 2x + 3 − y0 = 0(1)
+ Nếu y0 = 3 thì phương trình (1)trở thành: 2x = 0 ⇔ x = 0.
Vậy phương trình (1)có nghiệm y0 = 3(*).
+ Nếu y0 ≠ 3 thì phương trình (1)là phương trình bậc hai, nên nó có nghiệm khi và chỉ khi
Δ′ = 12 − (3−y0)2 ≥ 0
⇔ − y02 + 6y0 − 8 ≥ 0
⇔ 2 ≤ y0 ≤ 4.
Vậy phương trình (1)có nghiệm .
+ Kết hợp (*), (**) thì phương trình (1)có nghiệm ⇔ 2 ≤ y0 ≤ 4.
Vậy: Miền giá trị của hàm số là [2; 4].
Cách 2: Ta có
Suy ra GTNN của A = 2 khi và chỉ khi x = − 1.
Mặt khác
Suy ra GTLN của A = 4 khi và chỉ khi x = 1.
Vậy miền giá trị của hàm số là [2; 4].
Tìm tập xác định
Tập xác định của hàm số ![]() là:
là:
Điều kiện: 8 − 2x ≥ 0 ⇔ x ≤ 4. Vậy D = ( − ∞; 4].
Tim số nghiệm của phương trình
Số nghiệm của phương trình ![]() là
là
Điều kiện: .
⇔
⇔
⇔ ⇔ x = 0(TM).
Vậy, phương trình có một nghiệm.
Tìm tập xác định của hàm số
Tập xác định của hàm số ![]() là:
là:
Điều kiện xác định của hàm số là:
=> Tập xác định của hàm số là:
Chọn khẳng định sai
Cho hàm số y = f(x) có tập xác định là [ − 1; 5] và đồ thị của nó được biểu diễn bởi hình bên. Khẳng định nào sau đây là sai?
Trên khoảng (−1;1) và (2;3) đồ thị hàm số đi lên từ trái sang phải
Hàm số đồng biến trên khoảng (−1;1) và (2;3).
Trên khoảng (1;2) và (3;5) đồ thị hàm số đi xuống từ trái sang phải
Hàm số nghịch biến trên khoảng (1;2) và (3;5).
Tìm m để
Tìm m để phương trình ![]() có hai nghiệm phân biệt là:
có hai nghiệm phân biệt là:
Phương trình .
Phương trình đã cho có hai nghiệm ⇔ (*)có hai nghiệm phân biệt lớn hơn hoặc bằng đồ thị hàm số y = 3x2 + (4−m)x − 1 trên
cắt trục hoành tại hai điểm phân biệt.
Xét hàm số y = 3x2 + (4−m)x − 1 trên . Ta có
+ TH1: Nếu thì hàm số đồng biến trên
nên m ≤ 1 không thỏa mãn yêu cầu bài toán.
+ TH2: Nếu :
Ta có bảng biến thiên

Đồ thị hàm số y = 3x2 + (4−m)x − 1 trên cắt trục hoành tại hai điểm phân biệt
Vì − m2 + 8m − 28 = − (m−4)2 − 12 < 0, ∀m nên
(thỏa mãn m > 1).
Vậy là giá trị cần tìm.
Tìm m để bất phương trình vô nghiệm
Cho tam thức bậc hai ![]() . Tìm tất cả các giá trị thực của tham số m để bất phương trình
. Tìm tất cả các giá trị thực của tham số m để bất phương trình ![]() vô nghiệm?
vô nghiệm?
Bất phương trình: vô nghiệm khi và chỉ khi
Xét
Với thì (*)
loại giá trị
.
Với thì bất phương trình (*)
bất phương trình vô nghiệm, nhận giá trị
.
Xét
Vậy thì bất phương trình (*) vô nghiệm.
Trục đối xứng của hàm số bậc hai
Trong các hàm số sau, hàm số nào có đồ thị nhận đường x = 1 làm trục đối xứng?
Ta có đáp án có:
Vậy x = 1 là trục đối xứng của đồ thị hàm số .
Xác định giá trị tham số m thỏa mãn yêu cầu
Cho phương trình ![]() (
(![]() là tham số). Tìm
là tham số). Tìm ![]() để phương trình vô nghiệm.
để phương trình vô nghiệm.
Đặt . Khi đó ta có phương trình:
. (1)
Với thì
(Loại)
Với để phương trình ban đầu vô nghiệm thì:
TH1: (1) vô nghiệm .
TH2: (1) có 2 nghiệm âm
Kết hợp 2 trường hợp, ta được .
Tính số nghiệm của phương trình
Số nghiệm của phương trình ![]() là:
là:
ĐKXĐ: 60 − 24x − 5x2 ≥ 0
Đặt , (t≥0)pt trở thành
Vậy pt ban đầu có hai nghiệm .
Tìm m thỏa mãn điều kiện
Cho hàm số ![]() xác định trên [ − 1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [ − 1; 1] lần lượt là y1, y2 thỏa mãn y1 − y2 = 8. Khi đó giá trị của m bằng
xác định trên [ − 1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [ − 1; 1] lần lượt là y1, y2 thỏa mãn y1 − y2 = 8. Khi đó giá trị của m bằng
Đặt .
Hoành độ đỉnh của đồ thị hàm số là .
Vì hệ số a = 1 > 0 nên hàm số nghịch biến trên .
Suy ra, hàm số nghịch biến [ − 1; 1].
.
.
Theo đề bài ta có: y1 − y2 = 8
⇔ m2 − 2m + 1 = 0 ⇔ m = 1.
Tìm điểm thuộc đồ thị hàm số
Điểm nào sau đây thuộc đồ thị hàm số ![]() ?
?
Thay tọa độ vào
ta được
thỏa mãn. Suy ra điểm này thuộc đồ thị hàm số
.
Phương trình có nghiệm là
Phương trình ![]() có nghiệm là bao nhiêu?
có nghiệm là bao nhiêu?
.
Vậy phương trình vô nghiệm.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
