Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 10 Khóa học Lớp 10 Toán 10 - Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2

Mô tả thêm:

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 10 theo chương trình sách Kết nối tri thức nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 45 câu
  • Số điểm tối đa: 45 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
  • Câu 1: Nhận biết

    Xác định vectơ đối

    Cho hình bình hành ABCD. Các vectơ là vectơ đối của vectơ \overrightarrow{AD} là:

    Vectơ đối của vectơ \overrightarrow{AD} là \overrightarrow{DA},\overrightarrow{CB}.

  • Câu 2: Thông hiểu

    Tìm câu sai

    Cho hình thang vuông ABCDcó đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD . Câu nào sau đây sai?

    Phương án \overrightarrow{AB}.\overrightarrow{DC} = 8a^{2}: \overrightarrow{AB}.\overrightarrow{DC} =AB.DC.\cos0^{o} = 8a^{2} nên loại.

    Phương án \overrightarrow{AD}.\overrightarrow{CD} = 0: \overrightarrow{AD}\bot\overrightarrow{CD} suy ra \overrightarrow{AD}.\overrightarrow{CD} = 0 nên loại.

    Phương án \overrightarrow{AD}.\overrightarrow{AB} = 0: \overrightarrow{AD}\bot\overrightarrow{AB} suy ra \overrightarrow{AD}.\overrightarrow{AB} = 0 nên loại.

    Phương án \overrightarrow{DA}.\overrightarrow{DB} = 0: \overrightarrow{DA} không vuông góc với \overrightarrow{DB} suy ra \overrightarrow{DA}.\overrightarrow{DB} \neq 0 nên chọn.

  • Câu 3: Vận dụng

    Xác định giao của hai tập hợp

    Cho A = \left\{ \left. \ x\mathbb{\in N}\right|\left( 2x - x^{2} \right)\left( 2x^{2} - 3x - 2 \right) = 0\right\};B = \left\{ \left. \ n \in \mathbb{N}^{*} \right|3 < n^{2}< 30 \right\}. Khi đó tập hợp A \cap B bằng:

    Ta có:

    A = \left\{ \left. \ x\mathbb{\in N}\right|\left( 2x - x^{2} \right)\left( 2x^{2} - 3x - 2 \right) = 0\right\}

    \Leftrightarrow A = \left\{ 0;\ 2 \right\}

    B = \left\{ \left. \ n \in\mathbb{N}^{*} \right|3 < n^{2} < 30 \right\}

    \Leftrightarrow B =\left\{ 1;\ 2;\ 3;\ 4;5\ \right\} \Rightarrow A \cap B = \left\{ 2\right\}.

  • Câu 4: Thông hiểu

    Chọn câu đúng nhất

    Cho ba tập hợp: X = ( - 4;\ 3), Y = \left\{ x\mathbb{\in R}:2x + 4 > 0,\ x < 5\ \right\}, Z = \left\{ x\mathbb{\in R}:(x + 3)(x - 4) = 0\ \right\}. Chọn câu đúng nhất:

    Ta có:

    Y = \left\{ x\mathbb{\in R}:2x + 4 > 0,\ x < 5\ \right\} = ( - 2;\ 5); Z = \left\{ - 3;\ 4\ \right\}.

    \left\{ \begin{matrix} - 3 \in X \\ - 3 \notin Y \\ \end{matrix} \right.\ \Rightarrow X ⊄ Y \Rightarrow X \subset Y sai.

    \left\{ \begin{matrix}4 \in Z \\4 \notin X \\\end{matrix} \right.\ \Rightarrow Z ⊄ X \Rightarrow Z \subset X sai.

    \left\{ \begin{matrix} - 3 \in Z \\ - 3 \notin Y \\ \end{matrix} \right.\ \Rightarrow Z ⊄ Y \Rightarrow Z \subset Y sai.

    X \cup Y = ( - 4;5) \Rightarrow \left\{ - 3;4 \right\} \subset ( - 4;5).

    Vậy Z \subset X \cup Y là đáp án đúng nhất.

  • Câu 5: Vận dụng

    Tìm giá trị bất thường

    Hình dưới thống kê tỉ lệ phần trăm thất nghiệp ở một số quốc gia:

    Hãy tìm giá trị bất thường (nếu có) của mẫu số liệu.

    Sắp xếp các giá trị theo thứ tự không giảm:

    3,2 3,6 4,4 4,5 5,0 5,4 6,0 6,7 7,0 7,2 7,7 7,8 8,4 8,6 8,7

    Từ mẫu số liệu ta tính được: Q_{2} = 6,7 và Q_{1} = 4,5, Q_{3} = 7,8.

    Suy ra \Delta_{Q} = Q_{3} - Q_{1} = 7,8 - 4,5 = 3,3.

    Ta có: Q_{1} - 1,5\Delta_{Q} = 4,5 - 1,5.3,3 = - 0,45.

    Ta có: Q_{3} + 1,5\Delta_{Q} = 7,8 + 1,5.3,3 = 12,75.

    Ta thấy không có số liệu nào nhỏ hơn - 0,45 và lớn hơn 12,75 nên mẫu không có giá trị bất thường.

  • Câu 6: Vận dụng cao

    Chọn đáp án thích hợp

    Cho hai điểm A,\ \ B phân biệt và cố định, với I là trung điểm của AB. Tìm tập hợp các điểm M thỏa mãn đẳng thức \left| 2\overrightarrow{MA} + \overrightarrow{MB} \right| = \left| \overrightarrow{MA} + 2\overrightarrow{MB} \right|.

    Chọn điểm E thuộc đoạn AB sao cho EB = 2EA

    \Rightarrow 2\overrightarrow{EA} + \overrightarrow{EB} = \overrightarrow{0}.

    Chọn điểm F thuộc đoạn AB sao cho FA = 2FB

    \Rightarrow 2\overrightarrow{FB} + \overrightarrow{FA} = \overrightarrow{0}.

    Ta có \left| 2\overrightarrow{MA} + \overrightarrow{MB} \right| = \left| \overrightarrow{MA} + 2\overrightarrow{MB} \right|

    \Leftrightarrow \left| 2\overrightarrow{ME} + 2\overrightarrow{EA} + \overrightarrow{ME} + \overrightarrow{EB} \right| = \left| 2\overrightarrow{MF} + 2\overrightarrow{FB} + \overrightarrow{MF} + \overrightarrow{FA} \right|

    \Leftrightarrow \left| 3\ \overrightarrow{ME} + \underset{\overrightarrow{0}}{\overset{2\ \overrightarrow{EA} + \overrightarrow{EB}}{︸}} \right| = \left| 3\ \overrightarrow{MF} + \underset{\overrightarrow{0}}{\overset{2\ \overrightarrow{FA} + \overrightarrow{FB}}{︸}} \right|

    \Leftrightarrow \left| 3\ \overrightarrow{ME} \right| = \left| 3\ \overrightarrow{MF} \right| \Leftrightarrow ME = MF\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (*).

    Vì E,\ \ F là hai điểm cố định nên từ đẳng thức (*) suy ra tập hợp các điểm M là trung trực của đoạn thẳng EF.

    Gọi I là trung điểm của AB suy ra I cũng là trung điểm của EF. lời g

    Vậy tập hợp các điểm M thỏa mãn \left| 2\overrightarrow{MA} + \overrightarrow{MB} \right| = \left| \overrightarrow{MA} + 2\overrightarrow{MB} \right| là đường trung trực của đoạn thẳng AB.

  • Câu 7: Thông hiểu

    Chọn kết luận đúng

    Cho tam giác ABC có a^{2} + b^{2} - c^{2} > 0. Khi đó:

    Ta có:

    \cos C = \frac{a^{2} + b^{2} - c^{2}}{2ab}.

    Mà: a^{2} + b^{2} - c^{2} > 0 suy ra: \cos C > 0 \Rightarrow C < 90^{0}.

  • Câu 8: Nhận biết

    Tìm khẳng định đúng

    Cho hai tập hợp A = \left\{ 1;2;3;7 \right\},\ \ B = \left\{ 2;4;6;7;8 \right\}. Khẳng định nào sau đây đúng?

    Ta có \left\{ \begin{matrix} A \cap B = \left\{ 2;7 \right\} \\ A \cup B = \left\{ 1;2;3;4;6;7;8 \right\} \\ A\backslash B = \left\{ 1;3 \right\} \\ B\backslash A = \left\{ 4;6;8 \right\} \\ \end{matrix} \right..

  • Câu 9: Vận dụng cao

    Tìm số học sinh thỏa mãn yêu cầu

    Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?

    Gọi T, L, H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa.

    Khi đó tương tự Ví dụ 13 ta có công thức:

    A black background with a black and white logoDescription automatically generated

    |T \cup L \cup H| = |T| + |L| + |H| - |T \cap L| - |L \cap H| - |H \cap T| + |T \cap L \cap H|

    \Leftrightarrow 45 = 25 + 23 + 20 - 11 - 8 - 9 + |T \cap L \cap H| \Leftrightarrow |T \cap L \cap H| = 5

    Vậy có 5 học sinh giỏi cả 3 môn.

  • Câu 10: Nhận biết

    Xác định nghiệm bất phương trình

    Cặp số nào sau đây là nghiệm của bất phương trình - 5x + y \geq 5 ?

    Thay các cặp số vào bất phương trình ta thấy (0;5) là nghiệm của bất phương trình đã cho.

  • Câu 11: Thông hiểu

    Chọn biểu thức tính độ dài đường trung tuyến tam giác

    Độ dài trung tuyến m_{c} ứng với cạnh c của \Delta ABC bằng biểu thức nào sau đây?

    Ta có:

    m_{c}^{2} = \frac{b^{2} + a^{2}}{2} - \frac{c^{2}}{4}

    \Rightarrow m_{c} = \sqrt{\frac{b^{2} + a^{2}}{2} - \frac{c^{2}}{4}} = \frac{1}{2}\sqrt{(2b^{2} + 2a^{2}) - c^{2}}.

  • Câu 12: Nhận biết

    Chọn kết quả đúng

    Cho \overrightarrow{a} và \overrightarrow{b} là hai vectơ cùng hướng và đều khác vectơ \overrightarrow{0}.Trong các kết quả sau đây,hãy chọn kết quả đúng.

    Ta thấy vế trái của 4 phương án giống nhau.

    Bài toán cho \overrightarrow{a} và \overrightarrow{b} là hai vectơ cùng hướng và đều khác vectơ \overrightarrow{0} suy ra \left( \overrightarrow{a},\overrightarrow{b} ight) = 0^{0}

    Do đó \overrightarrow{a}.\overrightarrow{b} = \left| \overrightarrow{a} ight|.\left| \overrightarrow{b} ight|.cos0^{o} = \left| \overrightarrow{a} ight|.\left| \overrightarrow{b} ight| nên

  • Câu 13: Vận dụng

    M thuộc miền nghiệm của bất phương trình nào

    Điểm M(0; -3) thuộc miền nghiệm của hệ bất phương trình nào sau đây?

    Thay tọa độ M vào hệ bất phương trình \left\{\begin{matrix}2x-y\leq 3\\ 2x+5y\leq 12x+8\end{matrix}ight. ta được:

    \left\{ {\begin{array}{*{20}{c}} {2.0 - \left( { - 3} ight) \leqslant 3} \\ {2.0 + 5.\left( { - 3} ight) \leqslant 12.0 + 8} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {3 \leqslant 3} \\ { - 15 \leqslant 8} \end{array}\left( {TM} ight)} ight.

    Vậy điểm M(0; -3) thuộc miền nghiệm của hệ bất phương trình.

    Thay tọa độ M vào hệ bất phương trình \left\{\begin{matrix}2x-y> 3\\ 2x+5y\leq 12x+8\end{matrix}ight. ta được:

    \left\{ {\begin{array}{*{20}{c}} {2.0 - \left( { - 3} ight) > 3} \\ {2.0 + 5.\left( { - 3} ight) \leqslant 12.0 + 8} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {3 > 3} \\ { - 15 \leqslant 8} \end{array}\left( L ight)} ight.

    Vậy điểm M(0; -3) không thuộc miền nghiệm của hệ bất phương trình.

    Thay tọa độ M vào hệ bất phương trình \left\{\begin{matrix}2x-y<- 3\\ 2x+5y\leq 12x+8\end{matrix}ight. ta được:

    \left\{ {\begin{array}{*{20}{c}} {2.0 - \left( { - 3} ight) < - 3} \\ {2.0 + 5.\left( { - 3} ight) \leqslant 12.0 + 8} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {3 < - 3} \\ { - 15 \leqslant 8} \end{array}\left( L ight)} ight.

    Vậy điểm M(0; -3) không thuộc miền nghiệm của hệ bất phương trình.

    Thay tọa độ M vào hệ bất phương trình \left\{\begin{matrix}2x-y\leq -3\\ 2x+5y\leq 12x+8\end{matrix}ight. ta được:

    \left\{ {\begin{array}{*{20}{c}} {2.0 - \left( { - 3} ight) \leqslant - 3} \\ {2.0 + 5.\left( { - 3} ight) \leqslant 12.0 + 8} \end{array}} ight. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {3 \leqslant - 3} \\ { - 15 \leqslant 8} \end{array}\left( L ight)} ight.

    Vậy điểm M(0; -3) không thuộc miền nghiệm của hệ bất phương trình.

  • Câu 14: Thông hiểu

    Tìm điểm không thuộc miền nghiệm

    Miền nghiệm của bất phương trình - 3x - 5y < - 1 không chứa điểm nào sau đây?

    Xét điểm ( - 1; - 1). Ta có: - 3( - 1) - 5( - 1) = 8 < - 1 không thỏa mãn. Do đó ( - 1; - 1) không thuộc miền nghiệm của bất phương trình.

  • Câu 15: Nhận biết

    Tìm tọa độ vectơ

    Cho \overrightarrow{a} = (3; - 4),\overrightarrow{b} = ( - 1;2). Tọa độ của vec tơ \overrightarrow{a} + \overrightarrow{b} là:

    Ta có: \overrightarrow{a} + \overrightarrow{b} = \left( 3 + ( - 1);( - 4) + 2 \right) = (2; - 2).

  • Câu 16: Thông hiểu

    Tìm điểm thỏa mãn

    Miền nghiệm của hệ bất phương trình \left\{ \begin{matrix} x + y \geq 9 \\ 2x \geq y - 3 \\ 2y \geq x \\ y \leq 6 \\ \end{matrix} ight. chứa điểm nào trong các điểm sau đây?

    Với P(8;4). Ta có: \left\{ \begin{matrix} 8 + 4 \geq 9 \\ 2.8 \geq 4 - 3 \\ 2.4 \geq 8 \\ 4 \leq 6 \\ \end{matrix} ight.. Cả 4 bất phương trình đều đúng. Chọn đáp án này.

  • Câu 17: Vận dụng

    Tìm 3 điểm thẳng hàng

    Cho 4 điểm A(1; - 2),B(0;3),C( - 3;4),D( - 1;8). Ba điểm nào trong 4 điểm đã cho là thẳng hàng?

    Ta có: \overrightarrow{AD}( - 2;10),\ \overrightarrow{AB}( - 1;5) \Rightarrow \overrightarrow{AD} = 2\overrightarrow{AB} \Rightarrow 3 điểm A,B,D thẳng hàng.

  • Câu 18: Vận dụng

    Tìm bất phương trình thỏa mãn

    Tìm bất phương trình thỏa mãn miền được tô màu xám. (không kể bờ d)

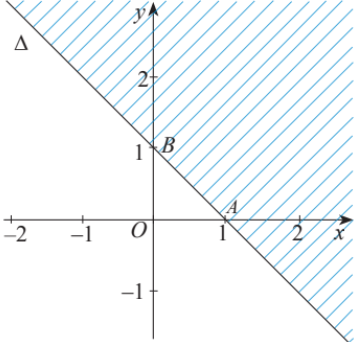
    Đường thẳng d có dạng y = ax + b đi qua hai điểm ( - 1;0) và (0,1).

    Thay tọa độ hai điểm này vào d: \left\{ \begin{matrix} 0 = a. - 1 + b \\ 1 = a.0 + b \\ \end{matrix} \Rightarrow \left\{ \begin{matrix} a = 1 \\ b = 1 \\ \end{matrix} ight.\ ight..

    Vậy d có dạng y = x + 1 \Leftrightarrow x - y + 1 = 0.

    Thay điểm O(0;0) vào d : 0 - 0 + 1 > 0. Suy ra phần màu xám (không chứa O) là nghiệm của bất phương trình x - y + 1 < 0.

  • Câu 19: Nhận biết

    Tìm một mệnh đề

    Phát biểu nào sau đây là một mệnh đề?

    Phát biểu ở “Mùa thu Hà Nội đẹp quá!”; “Bạn có đi học không?”; “Đề thi môn Toán khó quá1” là câu cảm và câu hỏi nên không là mệnh đề.

    Vậy mệnh đề cần tìm là: “Hà Nội là thủ đô của Việt Nam”.

  • Câu 20: Vận dụng cao

    Tìm giá trị lớn nhất

    Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II. Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là.

    Gọi x, y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x, y nguyên dương.

    Ta có hệ bất phương trình sau: \left\{ \begin{matrix} 3x + 2y \leq 180 \\ x + 6y \leq 220 \\ x > 0 \\ y > 0 \\ \end{matrix} ight.

    Miền nghiệm của hệ trên là

    Tiền lãi trong một tháng của xưởng là T = 0,5x + 0,4y .

    Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A, B, C. Vì C có tọa độ không nguyên nên loại.

    Tại A(60;\ 0) thì T = 30 triệu đồng.

    Tại B(40;\ 30) thì T = 32 triệu đồng.

    Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

  • Câu 21: Thông hiểu

    Thực hiện phép tính

    Kết quả bài toán tính: \overrightarrow{AB} + \overrightarrow{CD} - \overrightarrow{AD} là:

    Ta có:

    \overrightarrow{AB} + \overrightarrow{CD} - \overrightarrow{AD}

    = \overrightarrow{AB} - \overrightarrow{AD} + \overrightarrow{CD} = \overrightarrow{DB} + \overrightarrow{CD} = \overrightarrow{CB}.

  • Câu 22: Thông hiểu

    Khẳng định nào sau đây là đúng?

    Cho \overrightarrow{u} = (3; - 2),\ \overrightarrow{v} = (1;6). Khẳng định nào sau đây là đúng?

    Ta có \overrightarrow{u} + \overrightarrow{v} = (4;4) và \overrightarrow{u} - \overrightarrow{v} = (2; - 8).

    Xét tỉ số \frac{4}{- 4} eq \frac{4}{4}\overset{}{ightarrow}\overrightarrow{u} + \overrightarrow{v} và \overrightarrow{a} = ( - 4;4) không cùng phương. Loại \overrightarrow{u} + \overrightarrow{v} và \overrightarrow{a} = ( - 4;4) ngược hướng.

    Xét tỉ số \frac{3}{1} eq \frac{- 2}{6}\overset{}{ightarrow}\overrightarrow{u},\ \overrightarrow{v} không cùng phương. Loại \overrightarrow{u},\ \overrightarrow{v} cùng phương.

    Xét tỉ số \frac{2}{6} = \frac{- 8}{- 24} = \frac{1}{3} > 0\overset{}{ightarrow}\overrightarrow{u} - \overrightarrow{v} và \overrightarrow{b} = (6; - 24) cùng hướng. Chọn \overrightarrow{u} - \overrightarrow{v} và \overrightarrow{b} = (6; - 24) cùng hướng.

  • Câu 23: Thông hiểu

    Cặp số nào là nghiệm của bất phương trình

    Cặp số nào sau đây là nghiệm của bất phương trình 3x - 5y > 12?

    Xét đáp án (0; 3) ta có: x = 0; y = 3 thay vào bất phương trình ta được:

    3.0 - 5.3 = - 15 < 12

    Vậy (0;3) không là cặp nghiệm của bất phương trình

    Xét đáp án (6; 1) ta có: x = 6; y = 1 thay vào bất phương trình ta được:

    3.6- 5.1=13> 12

    Vậy (6; 1) là cặp nghiệm của bất phương trình.

    Xét đáp án (2; 4) ta có: x = 2; y = 4 thay vào bất phương trình ta được:

    3.2 - 5.4 = - 14 < 12

    Vậy (2; 4) không là cặp nghiệm của bất phương trình.

    Xét đáp án (3; 2) ta có: x = 3; y = 2 thay vào bất phương trình ta được:

    3.3 - 5.2 = - 1 < 12

    Vậy (3; 2) không là cặp nghiệm của bất phương trình.

  • Câu 24: Nhận biết

    Tìm đẳng thức sai

    Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Đẳng thức nào sau đây sai?

    Đẳng thức sai là: \overrightarrow{OA} = \overrightarrow{OC}.

  • Câu 25: Thông hiểu

    Rút gọn biểu thức G

    Đơn giản biểu thức G = \left( 1 -\sin^{2}x \right)\cot^{2}x + 1 - \cot^{2}x:

    Ta có:

    G = \left\lbrack \left( 1 - \sin^{2}x\right) - 1 \right\rbrack \cot^{2}x + 1

    = - \sin^{2}x.\cot^{2}x + 1 = 1 - \cos^{2}x= \sin^{2}x.

  • Câu 26: Nhận biết

    Chọn đáp án đúng

    Cho số đúng \overline{a} = 40 \pm 0,5. Giá trị của \overline{a} thuộc đoạn nào sau đây?

    Ta có:

    \overline{a} = 40 \pm 0,5 \Rightarrow \overline{a} \in \lbrack 39,5;40,5brack

  • Câu 27: Vận dụng

    Tính độ dài vectơ

    Cho tam giác OAB vuông cân tại O, cạnh OA = a. Tính \left| 2\overrightarrow{OA} - \overrightarrow{OB} \right|.

    Hình vẽ minh họa

    Gọi C là điểm đối xứng của O qua A \Rightarrow OC = 2a.

    Tam giác OBC vuông tại O, có BC = \sqrt{OB^{2} + OC^{2}} = a\sqrt{5}.

    Ta có:

    2\overrightarrow{OA} - \overrightarrow{OB} = \overrightarrow{OC} - \overrightarrow{OB} = \overrightarrow{BC} suy ra \left| 2\overrightarrow{OA} - \overrightarrow{OB} \right| = \left| \overrightarrow{BC} \right| = a\sqrt{5}.

  • Câu 28: Nhận biết

    Tìm điều kiện để ba điểm thẳng hàng

    Cho ba điểm A,\ B,\ C phân biệt. Điều kiện cần và đủ để ba điểm đó thẳng hàng là

    Ta có tính chất: Điều kiện cần và đủ để ba điểm A,\ B,\ C phân biệt thẳng hàng là \exists k \in R:\overrightarrow{AB} = k\overrightarrow{AC}.

  • Câu 29: Thông hiểu

    Xác định kết quả phép toán tập hợp

    Cho hai tập hợp A = \left( \sqrt{2}; + \infty \right) và B = \left( - \infty;\frac{\sqrt{5}}{2} \right\rbrack. Khi đó (A \cap B) \cup (B\backslash A) là

    Biểu diễn hai tập hợp trên trục số như sau:

    Ta có A \cap B = \varnothing, B\backslash A = \left( - \infty;\frac{\sqrt{5}}{2} \right) .

    Do đó (A \cap B) \cup (B\backslash A) = \left( - \infty;\frac{\sqrt{5}}{2} \right)

  • Câu 30: Thông hiểu

    Tính giá trị của phương sai

    Có 100 học sinh tham dự kì thi học sinh giỏi Toán (thang điểm 20). Kết quả sau kì thi được thống kê như sau:

    Điểm

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    Tần số

    1

    1

    3

    5

    8

    13

    19

    24

    14

    10

    2

    Giá trị của phương sai gần bằng:

    Kết quả trung bình là:

    \overline x = \frac{{9.1 + 10.1 + 11.3 + 12.5 + 13.8 + 14.13 + 15.19 + 16.24 + 17.14 + 18.10 + 19.2}}{{100}} = 15,23

    Giá trị của phương sai là:

     \begin{matrix} {S^2} = \dfrac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + {n_3}{x_4}^2 + ... + {n_k}{x_k}^2} ight) - {\left( {\overline x } ight)^2} \hfill \\ \Rightarrow {S^2} = \dfrac{1}{{100}}({1.9^2} + {1.10^2} + {3.11^2} + {5.12^2} + {8.13^2} + {13.14^2} \hfill \\ + {19.15^2} + {24.16^2} + {14.17^2} + {10.18^2} + {2.19^2}) - {\left( {15,23} ight)^2} \hfill \\ \Rightarrow {S^2} \approx 3,96 \hfill \\ \end{matrix}

  • Câu 31: Nhận biết

    Tính số trung bình cộng

    Điểm kiểm tra môn Văn của bạn Lan là: 7; 9; 8; 9. Tính số trung bình cộng \overline{x} của mẫu số liệu trên.

    Số trung bình cộng của mẫu số liệu trên là: \overline{x} = \frac{7 + 9 + 8 + 9}{4} = 8,25.

  • Câu 32: Nhận biết

    Tính số đo góc A

    Cho tam giác ABC thỏa mãn: 2cosA = 1. Khi đó:

    Ta có: 2cosA = 1 \Leftrightarrow \cos A = \frac{1}{2} \Rightarrow \widehat{A} = 60^{0}.

  • Câu 33: Nhận biết

    Tính giá trị cotang của góc

    Giá trị cot\frac{\pi }{6} là:

     Ta có: cot\frac{\pi }{6} =\sqrt3.

  • Câu 34: Thông hiểu

    Tìm hệ thức sai

    Cho M,\ N,\ P,\ Q là bốn điểm tùy ý. Trong các hệ thức sau, hệ thức nào sai?

    Đáp án \overrightarrow{MN}\left( \overrightarrow{NP} + \overrightarrow{PQ} \right) = \overrightarrow{MN}.\overrightarrow{NP} + \overrightarrow{MN}.\overrightarrow{PQ} đúng theo tính chất phân phối.

    Đáp án \overrightarrow{MP}.\overrightarrow{MN} = - \overrightarrow{MN}.\overrightarrow{MP} sai. Sửa lại cho đúng \overrightarrow{MP}.\overrightarrow{MN} = \overrightarrow{MN}.\overrightarrow{MP}.

    Đáp án \overrightarrow{MN}.\overrightarrow{PQ} = \overrightarrow{PQ}.\overrightarrow{MN} đúng theo tính chất giao hoán.

    Đáp án \left( \overrightarrow{MN} - \overrightarrow{PQ} \right)\left( \overrightarrow{MN} + \overrightarrow{PQ} \right) = MN^{2} - PQ^{2}đúng theo tính chất phân phối.

  • Câu 35: Vận dụng

    Tính chiều cao của cột cờ

    Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.

    Tính chiều cao của cột cờ

    Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:

    Ta có: \widehat {CAB} = {180^0} - {51^0}40' = {128^0}20'

    Xét tam giác ABC ta có:

    \begin{matrix} \widehat {ABC} + \widehat {CAB} + \widehat {ACB} = {180^0} \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {\widehat {ABC} + \widehat {CAB}} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {180^0} - \left( {{{45}^0}39' + {{128}^0}20'} ight) \hfill \\ \Leftrightarrow \widehat {ACB} = {6^0}1\prime \hfill \\ \end{matrix}

    Áp dụng định lí sin trong tam giác ABC ta có:

    \begin{matrix} \dfrac{{AB}}{{\sin \widehat {ACB}}} = \dfrac{{AC}}{{\sin \widehat {ABC}}} = \dfrac{{BC}}{{\sin \widehat {CAB}}} \hfill \\ \Rightarrow \dfrac{{10}}{{\sin {6^0}1'}} = \dfrac{{AC}}{{\sin {{45}^0}39'}} \hfill \\ \Rightarrow AC = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}} \hfill \\ \end{matrix}

    Ta có tam giác ACH vuông tại C

    \begin{matrix} \Rightarrow CH = AC.\sin \widehat {HAC} \hfill \\ \Rightarrow CH = \dfrac{{10.\sin {{45}^0}39'}}{{\sin {6^0}1'}}.\sin {51^0}40' \approx 53,51\left( m ight) \hfill \\ \end{matrix}

    Chiều cao của cột cờ khoảng: 1,5+53,51=55,01(m)

  • Câu 36: Thông hiểu

    Khẳng định nào sau đây đúng?

    Cho tam giác ABC có M là trung điểm của BC,\ \ \ G là trọng tâm của tam giác ABC. Khẳng định nào sau đây đúng?

    Vì G là trọng tâm của tam giác ABC nên \overrightarrow{AG} = \frac{2}{3}\overrightarrow{AM}. Vì M là trung điểm của BC nên \overrightarrow{AB} + \overrightarrow{AC} = 2\ \overrightarrow{AM} \Leftrightarrow \overrightarrow{AM} = \frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} ight). Do đó \overrightarrow{AG} = \frac{2}{3}.\frac{1}{2}\left( \overrightarrow{AB} + \overrightarrow{AC} ight) = \frac{1}{3}\left( \overrightarrow{AB} + \overrightarrow{AC} ight).

  • Câu 37: Vận dụng

    Đẳng thức nào sau đây sai?

    Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai?

    Xét các đáp án:

    Đáp án \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = \overrightarrow{0}. Ta có \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = \left( \overrightarrow{OA} + \overrightarrow{OC} ight) + \left( \overrightarrow{OB} + \overrightarrow{OD} ight) = \overrightarrow{0}.

    Đáp án \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{AD}. Ta có \overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC} (quy tắc hình bình hành).

    Đáp án \left| \overrightarrow{BA} + \overrightarrow{BC} ight| = \left| \overrightarrow{DA} + \overrightarrow{DC} ight|. Ta có \left\{ \begin{matrix} \left| \overrightarrow{BA} + \overrightarrow{BC} ight| = \left| \overrightarrow{BD} ight| = BD \\ \left| \overrightarrow{DA} + \overrightarrow{DC} ight| = \left| \overrightarrow{DB} ight| = BD \\ \end{matrix} ight..

    Đáp án \overrightarrow{AB} + \overrightarrow{CD} = \overrightarrow{AB} + \overrightarrow{CB}. Do \overrightarrow{CD} eq \overrightarrow{CB} \Rightarrow \left( \overrightarrow{AB} + \overrightarrow{CD} ight) eq \left( \overrightarrow{AB} + \overrightarrow{CB} ight). Chọn đáp án này.

  • Câu 38: Vận dụng cao

    Tìm điều kiện góc C để diện tích tam giác đạt max

    Tam giác ABC có BC = a và CA=b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

    Diện tích tam giác ABC là

    S_{\Delta ABC} =\frac{1}{2}.AC.BC.\sin\widehat{ACB} =\frac{1}{2}.ab.\sin\widehat{ACB}.

    Vì a,\ \ b không đổi và \sin\widehat{ACB} \leq 1, \forall C nên suy ra S_{\Delta ABC} \leq \frac{ab}{2}.

    Dấu "=" xảy ra khi và chỉ khi \sin\widehat{ACB} = 1 \Leftrightarrow \widehat{ACB} = 90^{0}.

    Vậy giá trị lớn nhất của diện tích tam giác ABC là S = \frac{ab}{2}.

  • Câu 39: Vận dụng

    Xác định dấu của biểu thức

    Cho \frac{\pi}{2} < \alpha < \pi. Xác định dấu của biểu thức M = \cos\left( - \frac{\pi}{2} + \alpha ight).tan(\pi - \alpha).

    Ta có:

    \left\{ \begin{matrix} \frac{\pi}{2} < \alpha < \pi ightarrow 0 < - \frac{\pi}{2} + \alpha < \frac{\pi}{2} \\ \frac{\pi}{2} < \alpha < \pi ightarrow 0 < \pi - \alpha < \frac{\pi}{2} \\ \end{matrix} ight. \overset{}{ightarrow}\cos\left( - \frac{\pi}{2} + \alpha ight) > 0 và \overset{}{ightarrow}\tan(\pi - \alpha) > 0

    \overset{}{ightarrow}M > 0.

  • Câu 40: Thông hiểu

    Tính số trung bình cộng

    Bạn Bình ghi lại bảng thống kê số sách mà mà mỗi bạn học sinh lớp 10A đã đọc trong năm 2023. Hỏi trung bình mỗi bạn trong lớp đọc bao nhiêu cuốn sách?

    Số học sinh lớp 10A là: 3 + 5 + 15 + 10 + 7 = 40 (bạn).

    Trung bình mỗi bạn đọc: \overline{x} =\frac{3.1 + 5.2 + 15.3 + 4.10 + 7.5}{40}= 3,325 (cuốn sách).

  • Câu 41: Thông hiểu

    Tìm mệnh đề phủ định của P

    Mệnh đề phủ định của mệnh đề  là

    Mệnh đề phủ định của mệnh đề là:  \overline{P}:"\exists x\mathbb{\in R}:x^{2} + 1 \leq 2x". 

  • Câu 42: Nhận biết

    Chọn đẳng thức đúng

    Cho các điểm phân biệt A,B,C. Đẳng thức nào sau đây đúng?

    Ta có:

    \overrightarrow{AB} = \overrightarrow{AC} + \overrightarrow{CB} = \overrightarrow{CB} + \overrightarrow{AC} .

    Vậy khẳng định đúng cần tìm là: \overrightarrow{AB} = \overrightarrow{CB} + \overrightarrow{AC} .

  • Câu 43: Thông hiểu

    Tính diện tích hình chữ nhật đã cho

    Cho hình chữ nhật ABCD. Gọi AL và CI tương ứng là đường cao của các tam giác ADB và BCD. Cho biết DL = LI = IB = 1. Diện tích của hình chữ nhật ABCD (chính xác đến hàng phần trăm) là:

    Hình vẽ minh họa:

    Ta có: AL^{2} = BL.LD = 2

    do đó AL = \sqrt{2}.

    Lại có BD = 3

    Suy ra diện tích của hình chữ nhật là:

    3\sqrt{2} = 3.1,41421356... \approx 4,24264... \approx 4,24

  • Câu 44: Nhận biết

    Tìm khoảng tứ phân vị

    Chiều cao của một số học sinh nữ lớp 9 (đơn vị cm) được cho trong bảng.

    Tìm khoảng tứ phân vị của mẫu số liệu này.

    Nhận thấy mẫu đã được sắp xếp theo thứ tự không giảm.

    Số liệu chính giữa là 162 nên Q_{2} = 162.

    Số liệu chính giữa của mẫu 151 152 153 154 155 160 160 là 154 nên Q_{1} = 154.

    Số liệu chính giữa của mẫu 163 165 165 165 166 167 167 là 165 nên Q_{3} = 165.

    Khoảng tứ phân vị \Delta_{Q} = Q_{3} - Q_{1} = 165 - 154 = 11.

  • Câu 45: Nhận biết

    Tìm điểm thỏa mãn

    Cho hệ bất phương trình \left\{ \begin{matrix} x + 3y - 2 \geq 0 \\ 2x + y + 1 \leq 0 \\ \end{matrix} ight.. Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?

    Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

    Với M(0;1) \Rightarrow \left\{ \begin{matrix} 0 + 3.1 - 2 \geq 0 \\ 2.0 + 1 + 1 \leq 0 \\ \end{matrix} ight..Bất phương trình thứ hai sai nên không thỏa mãn.

    Với N(–1;1) \Rightarrow \left\{ \begin{matrix} - 1 + 3.1 - 2 \geq 0 \\ 2.( - 1) + 1 + 1 \leq 0 \\ \end{matrix} ight.. Đúng.

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
Tải file làm trên giấy
1
34 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 1 Toán 10 Kết nối tri thức Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/45
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này