Tích của vectơ với một số
Tích của một vectơ 
\(\overrightarrow a \neq \overrightarrow 0\)với số thực \(k\neq0\) là một vectơ có:
- Kí hiệu là \(k\overrightarrow a\).
- Phương cùng phương với vectơ \(\overrightarrow a\).
- Cùng hướng với \(\overrightarrow a\) nếu \(k>0\), ngược hướng với \(\overrightarrow a\) nếu \(k<0\).
- Độ dài bằng \(\left | k \right | \left|\overrightarrow a\right|\).
Quy ước: \(0.\overrightarrow a=\overrightarrow 0\) và \(k.\overrightarrow 0=\overrightarrow 0\).
Nhận xét:
- \(1.\overrightarrow a=\overrightarrow a\) và \((-1)\overrightarrow a=-\overrightarrow a\).
- \(I\) là trung điểm đoạn thẳng \(AB\) thì \(\overrightarrow {MA}+\overrightarrow {MB}=2\overrightarrow {MI}\)(với điểm \(M\) tùy ý).
- \(G\) là trọng tâm tam giác \(ABC\) thì \(\overrightarrow {MA}+\overrightarrow {MB}+\overrightarrow {MC}=3\overrightarrow {MG}\)(với điểm \(M\) tùy ý).
2. Tính chất
Với hai vectơ \(\overrightarrow {a},\overrightarrow {b}\) bất kì và mọi số thực \(k,l\) ta có:
- \(k(m\overrightarrow {a})=(km)\overrightarrow {a}\)
- \(k(\overrightarrow {a}+\overrightarrow {b})=k\overrightarrow {a}+k\overrightarrow {b}\)
- \((k+m)\overrightarrow {a}=k\overrightarrow {a}+m\overrightarrow {a}\)
3. Điều kiện để hai vectơ cùng phương
Hai vectơ \(\overrightarrow {a}\) và \(\overrightarrow {b}\) cùng phương khi và chỉ khi tồn tại số thực \(k\) sao cho \(\overrightarrow {a}=k\overrightarrow {b}\)(điều kiện \(\overrightarrow {b} \neq \overrightarrow {0}\).
Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi tồn tại số thực \(k\neq0\) sao cho \(\overrightarrow {AB}=k\overrightarrow {AC}\).
Chú ý: Cho hai vectơ \(\overrightarrow {a}\) và \(\overrightarrow {b}\) không cùng phương thì với mọi vectơ \(\overrightarrow {c}\), luôn tồn tại duy nhất cặp số \((m;n)\) sao cho \(\overrightarrow {c}=m\overrightarrow {a}+n\overrightarrow {b}\).
Ví dụ 1: Cho hình bình hành \(ABCD\). Gọi \(E\) là trung điểm \(CD\). Hãy biểu thị vectơ \(\overrightarrow {AE}\) theo hai vectơ \(\overrightarrow {AB}\) và \(\overrightarrow {AD}\).
Hướng dẫn giải
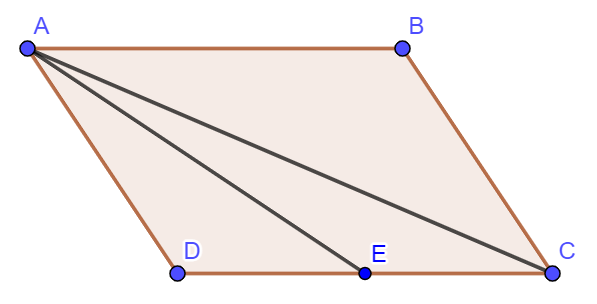
Vì \(E\) là trung điểm \(CD\) nên \(\overrightarrow {AC}+\overrightarrow {AD}=2\overrightarrow {AE}\) hay \(\overrightarrow {AE}=\frac12(\overrightarrow {AC}+\overrightarrow {AD})\).
Áp dụng quy tắc hình bình hành: \(\overrightarrow {AC}=\overrightarrow {AB}+\overrightarrow {AD}\).
Do đó: \(\overrightarrow {AE}=\frac12(\overrightarrow {AC}+\overrightarrow {AD}) =\frac12(\overrightarrow {AB}+\overrightarrow {AD} +\overrightarrow {AD})\)\(=\frac12\overrightarrow {AB}+\overrightarrow {AD}\).
Ví dụ 2: Cho tam giác \(ABC\) có \(M,N,P\) lần lượt là trung điểm \(BC,CA,AB\). Chứng minh:
a) \(\overrightarrow {AP}+\frac12\overrightarrow {BC}=\overrightarrow {AN}\);
b) \(\overrightarrow {BC}+2\overrightarrow {MP}=\overrightarrow {BA}\).
Hướng dẫn giải
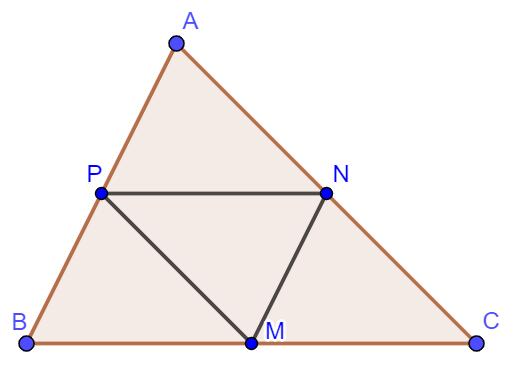
a) Ta có: \(\overrightarrow {AP}+\frac12\overrightarrow {BC}=\overrightarrow {AP}+\overrightarrow {PN}=\overrightarrow {AN}\)(Vì \(\overrightarrow {PN}=\overrightarrow {BM}=\frac12\overrightarrow {BC}\)).
b) Ta có: \(\overrightarrow {BC}+2\overrightarrow {MP}=\overrightarrow {BC}+\overrightarrow {CA}=\overrightarrow {BA}\) (Vì \(PM\) là đường trung bình trong tam giác \(BAC\) nên \(\overrightarrow {CA}=2\overrightarrow {MP}\)).
Ví dụ 3: Cho tam giác \(ABC\). Hãy tìm các điểm \(I,J\) thỏa mãn:
a) \(\overrightarrow {IA}+2\overrightarrow {IB}=\overrightarrow {0}\);
b) \(\overrightarrow {JA}+2\overrightarrow {JB}=2\overrightarrow {CB}\).
Hướng dẫn giải
a) \(\overrightarrow {IA}+2\overrightarrow {IB}=\overrightarrow {0} \Leftrightarrow \overrightarrow {IA}=-2\overrightarrow {IB}\)(2 vectơ ngược hướng).
Suy ra điểm \(I\) nằm giữa đoạn thẳng \(AB\) sao cho \(IA=2IB\).
Hình vẽ biểu diễn điểm \(I\):
b) \(\overrightarrow {JA}+2\overrightarrow {JB}=2\overrightarrow {CB}\)\(\Leftrightarrow \overrightarrow {JA}+2(\overrightarrow {JA}+\overrightarrow {AB})-2\overrightarrow {CB}=\overrightarrow 0\)
\(\Leftrightarrow 3\overrightarrow {JA}+2\overrightarrow {AB}+2\overrightarrow {BC} =\overrightarrow {0}\)\(\Leftrightarrow 3\overrightarrow {JA}+2\overrightarrow {AC}=\overrightarrow 0\)
\(\Leftrightarrow \overrightarrow {JA}=-\frac23 \overrightarrow {AC}\)\(\Leftrightarrow \overrightarrow {AJ}=\frac23 \overrightarrow {AC}\) (2 vectơ cùng hướng).
Suy ra điểm \(J\) nằm giữa đoạn \(AC\) sao cho \(AJ=\frac23AC\).
Hình vẽ biểu diễn điểm \(J\):
