Tính giá trị biểu thức
Cho biết ![]() , biểu thức
, biểu thức ![]() có giá trị là:
có giá trị là:
Ta có:
Cùng nhau thử sức với bài kiểm tra 45 phút Toán 11 CTST Chương 6: Hàm số mũ và hàm số lôgarit nha!
Tính giá trị biểu thức
Cho biết ![]() , biểu thức
, biểu thức ![]() có giá trị là:
có giá trị là:
Ta có:
Ghi lời giải vào chỗ trống
Bác A lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ trước được cộng vào vốn của kỳ kế tiếp) với kỳ hạn 3 tháng với lãi suất một quý. Đúng 6 tháng sau, bác A gửi thêm 100 triệu đồng với kỳ hạn và lãi suất không đổi. Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra. Hỏi tổng số tiền người đó nhận được sau 1 năm gửi tiền vào ngân hàng bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ hai).
Bác A lần đầu gửi vào ngân hàng 100 triệu đồng theo thể thức lãi kép (tức là tiền lãi của kỳ trước được cộng vào vốn của kỳ kế tiếp) với kỳ hạn 3 tháng với lãi suất một quý. Đúng 6 tháng sau, bác A gửi thêm 100 triệu đồng với kỳ hạn và lãi suất không đổi. Biết rằng trong suốt thời gian gửi tiền lãi suất ngân hàng không thay đổi và người đó không rút tiền ra. Hỏi tổng số tiền người đó nhận được sau 1 năm gửi tiền vào ngân hàng bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ hai).
Số tiền 100 triệu đồng gửi lần đầu thì sau 1 năm (4 quý) nhận được cả vốn lẫn lãi là:
triệu đồng
Số tiền 100 triệu đồng gửi lần thứ hai thì 6 tháng (2 quý) nhận được cả vốn lẫn lãi là:
triệu đồng
Vậy tổng số tiền nhận được là: triệu đồng.
Tìm y
Với các số thực dương x, y ta có: ![]() theo thứ tự lập thành một cấp số nhân và các số
theo thứ tự lập thành một cấp số nhân và các số ![]() theo thứ tự lập thành một cấp số cộng. Khi đó y bằng:
theo thứ tự lập thành một cấp số cộng. Khi đó y bằng:
Từ theo thứ tự lập thành một cấp số nhân nên công bội
Mặt khác theo thứ tự lập thành một cấp số cộng nên
Chọn mệnh đề đúng
Với a, b là các số thực dương tùy ý và a khác 1, đặt ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có:
Tính giá trị biểu thức
Ta có: ![]() . Biểu thức
. Biểu thức ![]() có giá trị là:
có giá trị là:
Ta có:
Thu gọn biểu thức B
Thu gọn biểu thức  với
với ![]() ta được:
ta được:
Ta có:
Tìm hàm số nghịch biến
Tìm hàm số nghịch biến trên tập số thực?
Ta có:
Hàm số có cơ số
nên hàm số nghịch biến trên
Hàm số có tập xác định
nên hàm số đồng biến trên
Hàm số có
nên hàm số nghịch biến trên
.
Hàm số có
nên hàm số đồng biến trên
.
Tính tỉ số a và b
Cho ![]() thỏa mãn
thỏa mãn ![]() . Xác định tỉ số
. Xác định tỉ số ![]() ?
?
Điều kiện
Với
Tìm hàm số nghịch biến
Trong các hàm số dưới đây, hàm số nào nghịch biến trên tập xác định của nó?
Hàm số có
là hàm số nghịch biến trên tập xác định của nó.
Các hàm số ;
;
có cơ số lớn hơn 1 nên đồng biến trên tập xác định của nó.
Biểu thức liên hệ giữa n và m
Cho các số thực dương phân biệt a và b. Biểu thức thu gọn của biểu thức
![P = \frac{{\sqrt a - \sqrt b }}{{\sqrt[4]{a} - \sqrt[4]{b}}} - \frac{{\sqrt {4a} + \sqrt[4]{{16ab}}}}{{\sqrt[4]{a} + \sqrt[4]{b}}}](/data/image/holder.png)
có dạng ![]() . Khi đó biểu thức liên hệ giữa n và m là:
. Khi đó biểu thức liên hệ giữa n và m là:
Ta có:
Ghi lời giải vào chỗ trống
Cho ![]() là các số thực thay đổi thỏa mãn
là các số thực thay đổi thỏa mãn ![]() và
và ![]() là các số thực dương thay đổi thỏa mãn
là các số thực dương thay đổi thỏa mãn ![]() . Tính giá trị nhỏ nhất của biểu thức
. Tính giá trị nhỏ nhất của biểu thức ![]() ?
?
Cho ![]() là các số thực thay đổi thỏa mãn
là các số thực thay đổi thỏa mãn ![]() và
và ![]() là các số thực dương thay đổi thỏa mãn
là các số thực dương thay đổi thỏa mãn ![]() . Tính giá trị nhỏ nhất của biểu thức
. Tính giá trị nhỏ nhất của biểu thức ![]() ?
?
Giải phương trình
Tìm nghiệm phương trình ![]() ?
?
Ta có:
Vậy phương trình có nghiệm .
Phân tích sự đúng sai của mỗi phát biểu
Xét tính đúng, sai của các phát biểu sau?
a) Hàm số ![]() luôn nghịch biến trên tập số thực. Đúng||Sai
luôn nghịch biến trên tập số thực. Đúng||Sai
b) Tập xác định của hàm số ![]() là
là ![]() Sai||Đúng
Sai||Đúng
c) Ta có: ![]() suy ra
suy ra ![]() Sai||Đúng
Sai||Đúng
d) Với ![]() thì hàm số
thì hàm số ![]() xác định trên
xác định trên ![]() . Đúng||Sai
. Đúng||Sai
Xét tính đúng, sai của các phát biểu sau?
a) Hàm số ![]() luôn nghịch biến trên tập số thực. Đúng||Sai
luôn nghịch biến trên tập số thực. Đúng||Sai
b) Tập xác định của hàm số ![]() là
là ![]() Sai||Đúng
Sai||Đúng
c) Ta có: ![]() suy ra
suy ra ![]() Sai||Đúng
Sai||Đúng
d) Với ![]() thì hàm số
thì hàm số ![]() xác định trên
xác định trên ![]() . Đúng||Sai
. Đúng||Sai
a) Vì nên hàm số
luôn nghịch biến trên tập số thực đúng.
b) Điều kiện xác định của hàm số:
Vậy tập xác định của hàm số là
c) Ta có: nên
hay
d) Điều kiện xác định:
TH1:
TH2:
Suy ra tập xác định của hàm số
Khi đó yêu cầu bài toán trở thành
Th3:
Suy ra tập xác định của hàm số
Do đó không tồn tại giá trị m thỏa mãn yêu cầu bài toán.
Điền đáp án vào ô trống
Có bao nhiêu giá trị nguyên của dương của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên tập số thực?
đồng biến trên tập số thực?
Đáp án: 4
Có bao nhiêu giá trị nguyên của dương của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên tập số thực?
đồng biến trên tập số thực?
Đáp án: 4
Hàm số đồng biến trên
khi và chỉ khi
Mà
Vậy có 4 giá trị của tham số m thỏa mãn điều kiện đề bài.
Tìm khẳng định đúng
Cho hai số thực dương ![]() thỏa mãn
thỏa mãn ![]() . Tìm khẳng định đúng dưới đây?
. Tìm khẳng định đúng dưới đây?
Ta có:
Chọn đáp án đúng
Tính giá trị biểu thức ![]() .
.
Ta có:
Rút gọn biểu thức H
Rút gọn biểu thức ![]() .
.
Ta có:
Tìm kết luận đúng
Cho ![]() là hai số thực dương bất kì và
là hai số thực dương bất kì và ![]() . Kết luận nào sau đây đúng?
. Kết luận nào sau đây đúng?
Theo tính chất ta suy ra kết luận đúng là:
Chọn kết luận đúng
Cho biểu thức  với
với ![]() . Kết quả sau khi đơn giản biểu thức C là:
. Kết quả sau khi đơn giản biểu thức C là:
Ta có:
Tính giá trị biểu thức
Cho ![]() . Khi đó
. Khi đó ![]() có giá trị là:
có giá trị là:
Ta có:
Tìm x để hàm số có nghĩa
Tìm tập xác định của hàm số ![]() là:
là:
Điều kiện xác định
Suy ra tập xác định của hàm số là: .
Chọn kết quả đúng
Với a là số thực dương tùy ý, ![]() bằng:
bằng:
Ta có:
Tìm các giá trị nguyên của m
Cho phương trình ![]() . Tìm tất cả các giá trị nguyên của tham số m để phương trình có hai nghiệm thực phân biệt
. Tìm tất cả các giá trị nguyên của tham số m để phương trình có hai nghiệm thực phân biệt ![]() thỏa mãn
thỏa mãn ![]() .
.
Đặt . Phương trình đã cho trở thành
Phương trình (*) có hai nghiệm phân biệt thỏa mãn
Tìm nghiệm của phương trình
Xác định nghiệm của phương trình ![]() ?
?
Ta có:
Vậy phương trình có nghiệm x = 1.
Chọn kết luận đúng
Giả sử ![]() , với
, với ![]() là phân số tối giản. Gọi
là phân số tối giản. Gọi ![]() . Kết luận nào dưới đây đúng?
. Kết luận nào dưới đây đúng?
Ta có:
Giải phương trình
Xác định nghiệm của phương trình ![]() ?
?
Ta có:
Vậy phương trình đã cho có nghiệm .
Tìm các giá trị của tham số m
Cho hàm số ![]() với
với ![]() là tham số. Tìm tất cả các giá trị thực của tham số
là tham số. Tìm tất cả các giá trị thực của tham số ![]() để hàm số đã
để hàm số đã ![]() xác định với mọi
xác định với mọi ![]() ?
?
Hàm số xác định với mọi
khi và chỉ khi
Vậy
Tìm tập xác định của hàm số
Cho hàm số ![]() . Tìm tập xác định của hàm số.
. Tìm tập xác định của hàm số.
Điều kiện xác định của hàm số là:
Vậy tập xác định của hàm số là:
Giá trị của biểu thức là
Giá trị của biểu thức ![]() là:
là:
Ta có:
Tính giá trị biểu thức H
Cho số thực dương a tùy ý. Viết biểu thức ![]() dưới dạng
dưới dạng ![]() trong đó
trong đó ![]() là phân số tối giản,
là phân số tối giản, ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có:
Biến đổi biểu thức
Cho ![]() là số thực dương. Viết
là số thực dương. Viết ![]() dưới dạng lũy thừa với số mũ hữu tỉ ta được:
dưới dạng lũy thừa với số mũ hữu tỉ ta được:
Ta có:
Giải phương trình logarit
Tìm nghiệm của phương trình ![]() ?
?
Điều kiện xác định:
Vậy phương trình có nghiệm .
Giải bất phương trình
Tìm tập nghiệm của bất phương trình ![]() ?
?
Ta có:
Vậy tập nghiệm của bất phương trình là
Xét tính đúng sai của các khẳng định
Vẽ được đồ thị của các hàm số sau. Các khẳng định dưới đây đúng hay sai?
a) Đồ thị ![]() có dạng bên:
có dạng bên: 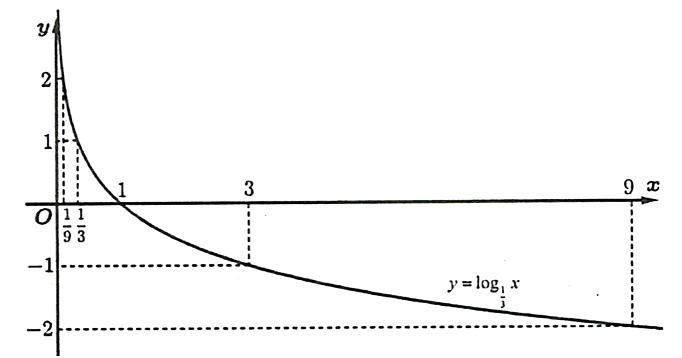 . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên: 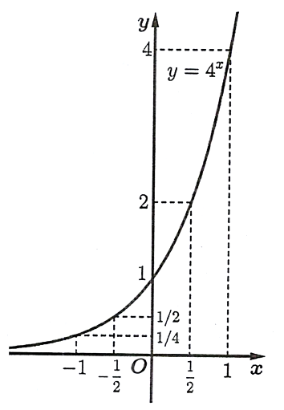 . Đúng||Sai
. Đúng||Sai
c) Đồ thị ![]() có dạng bên:
có dạng bên: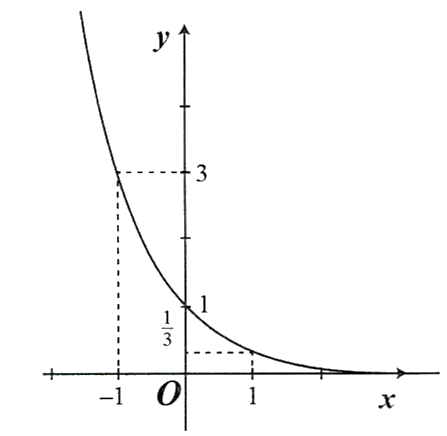 . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên: 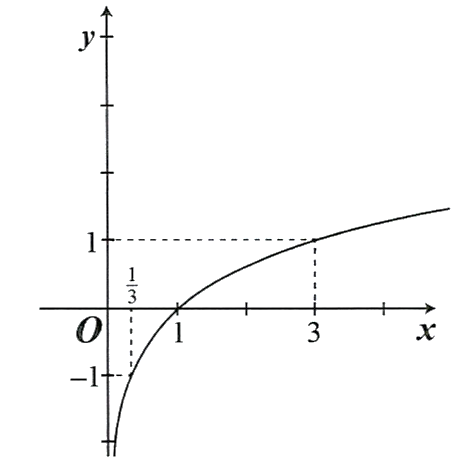 . Đúng||Sai
. Đúng||Sai
Vẽ được đồ thị của các hàm số sau. Các khẳng định dưới đây đúng hay sai?
a) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
c) Đồ thị ![]() có dạng bên:
có dạng bên: . Đúng||Sai
. Đúng||Sai
b) Đồ thị ![]() có dạng bên:
có dạng bên:  . Đúng||Sai
. Đúng||Sai
|
a) Đúng |
b) Đúng |
c) Đúng |
d) Đúng |
a) Hàm số có bảng giá trị:

Đồ thị của hàm số :
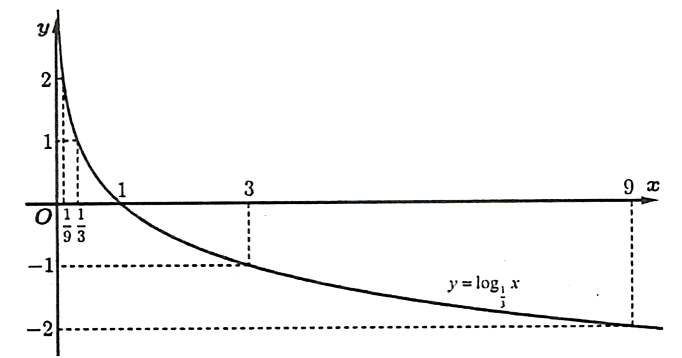
b) Hàm số có bảng giá trị:

Đồ thị của hàm số :
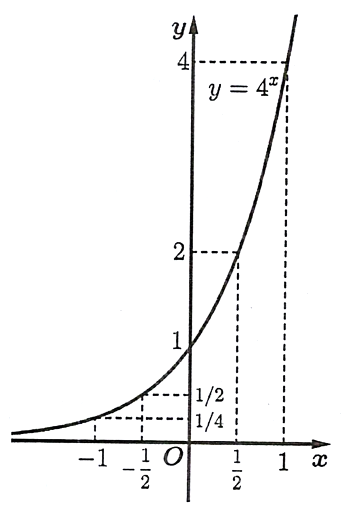
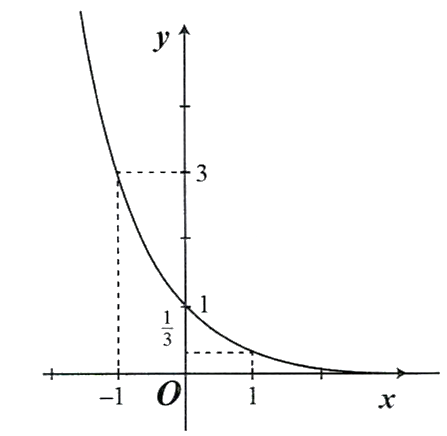
c) Hàm số nghịch biến trên
. Hàm số qua các điểm
,
và nằm trên trục hoành. Đồ thị:
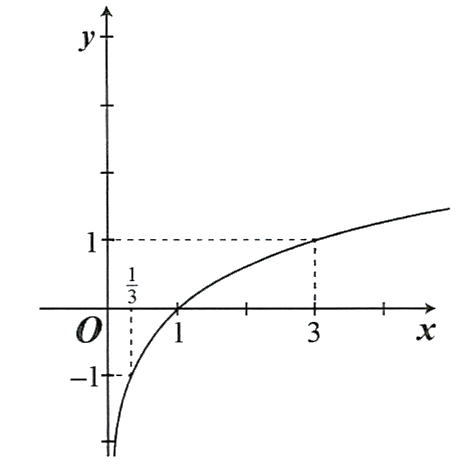
d) Hàm số đồng biến trên
. Hàm số qua các điểm
,
và nằm bên phải trục tung. Đồ thị:
Ghi đáp án vào ô trống
Cho đồ thị hàm số ![]() đối xứng với đồ thị hàm số
đối xứng với đồ thị hàm số ![]() như hình vẽ:
như hình vẽ:

Biết đồ thị hàm số ![]() qua điểm
qua điểm ![]() . Tính giá trị
. Tính giá trị ![]() ?
?
Đáp án: -2020|| - 2020
Cho đồ thị hàm số ![]() đối xứng với đồ thị hàm số
đối xứng với đồ thị hàm số ![]() như hình vẽ:
như hình vẽ:

Biết đồ thị hàm số ![]() qua điểm
qua điểm ![]() . Tính giá trị
. Tính giá trị ![]() ?
?
Đáp án: -2020|| - 2020
Vì đồ thị hàm số đối xứng với đồ thị hàm số
nên
có dạng
.
Gọi
là điểm đối xứng với qua điểm
.
Ta có:
Với
Khi đó:
Từ đó ta có:
Vậy
Chọn đáp án đúng
Cho phương trình ![]() . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
Điều kiện xác định
Lấy logarit cơ số 3 hai vế phương trình ta được:
Trường hợp 1: ta có:
. Phương trình vô nghiệm.
Trường hợp 2: ta có:
vô nghiệm
Vậy phương trình đã cho vô nghiệm.
Tính giá trị của biểu thức
Cho các số thức a, b thỏa mãn ![]() và
và ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]() ?
?
Ta có:
Đặt . Do
Khi đó
Với ta có:
=>
Tìm nghiệm nguyên của bất phương trình
Có bao nhiêu giá trị x nguyên thỏa mãn bất phương trình ![]() ?
?
Ta có:
Mà
Vậy có duy nhất 1 giá trị nguyên của x thỏa mãn yêu cầu đề bài.
Xác định tham số m
Tìm m để bất phương trình ![]() vô nghiệm.
vô nghiệm.
Ta có:
Bất phương trình vô nghiệm khi:
Xác định x để hàm số có nghĩa
Tìm tập xác định của hàm số ![]() ?
?
Hàm số xác định khi
Vậy tập xác định của hàm số là
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
