Hàm số lượng giác và đồ thị CTST

Loại	Định nghĩa	Kí hiệu	Tập xác định
Hàm số sin	quy tắc đặt tương ứng với mỗi số thực x với số thực sinx	\(y = \sin x\)	\(\mathbb{R}\)
Hàm số cosin	quy tắc đặt tương ứng với mỗi số thực x với số thực cosx	\(y = \cos x\)	\(\mathbb{R}\)
Hàm số tang	được cho bằng công thức  \(y = \frac{{\sin x}}{{\cos x}}\)	\(y = \tan x\)	\(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\)
Hàm số cotang	được cho bằng công thức \(y = \frac{{\cos x}}{{\sin x}}\)	\(y = \cot x\)	\(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\)

Ví dụ: Tìm tập xác định của hàm số:

a. \(y = \frac{{1 - 2{x^2}}}{{1 - \cos 2x}}\)	b. \(y = \sqrt {2 - 2\sin x}\)
c. \(y = \tan \left( {x + \frac{\pi }{4}} \right)\)	d. \(y = \cot \left( {\frac{\pi }{4} - 2x} \right) - \frac{2}{{1 - \cos x}}\)

Hướng dẫn giải

a) Hàm số \(y = \frac{{1 - 2{x^2}}}{{1 - \cos 2x}}\) xác định khi và chỉ khi

\(\begin{matrix} 1 - \cos 2x \ne 0 \Leftrightarrow \cos 2x \ne 1 \hfill \\ \Leftrightarrow 2x \ne k2\pi \Leftrightarrow x \ne k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}\)

Vậy tập xác định của hàm số \(D = \mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\)

b) Hàm số \(y = \sqrt {2 - 2\sin x}\) xác định khi và chỉ khi

\(2 - 2\sin x \geqslant 0 \Leftrightarrow \sin x \leqslant 1\) luôn đúng với \(\forall x \in \mathbb{R}\)

Vậy tập xác định của hàm số \(D = \mathbb{R}\).

c) Hàm số \(y = \tan \left( {x + \frac{\pi }{4}} \right)\) xác định khi và chỉ khi

\(\begin{matrix} \cos \left( {x + \dfrac{\pi }{4}} \right) \ne 0 \hfill \\ \Leftrightarrow x + \dfrac{\pi }{4} \ne \dfrac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \Leftrightarrow x \ne \dfrac{\pi }{4} + k\pi ;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}\)

Vậy tập xác định của hàm số \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\pi |k \in \mathbb{Z}} \right\}\).

d) Hàm số \(y = \cot \left( {\frac{\pi }{4} - 2x} \right) - \frac{2}{{1 - \cos x}}\) xác định khi và chỉ khi

\(\begin{matrix} \left\{ \begin{gathered} \sin \left( {\dfrac{\pi }{4} - 2x} \right) \ne 0 \hfill \\ 1 - \cos x \ne 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \dfrac{\pi }{4} - 2x \ne k\pi \hfill \\ \cos x \ne 1 \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow \left\{ \begin{gathered} x \ne \dfrac{\pi }{8} - \dfrac{{k\pi }}{2} \hfill \\ x \ne k2\pi \hfill \\ \end{gathered} \right.;\left( {k \in \mathbb{Z}} \right) \hfill \\ \end{matrix}\)

Vậy tập xác định của hàm số \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{8} - \frac{{k\pi }}{2};k2\pi |k \in \mathbb{Z}} \right\}\).

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a) Hàm số chẵn, hàm số lẻ

Chú ý:

• Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
• Đồ thị của một hàm số lẻ nhận trục hoành làm trục đối xứng.

Ví dụ: Xét tính chẵn lẻ của các hàm số sau:

a) \(y = 2x.\sin x\)

b) \(y = \cos x + \sin 2x\)

c) \(y = \frac{{\cos 2x}}{x}\)

Hướng dẫn giải

a) Tập xác định \(D = \mathbb{R}\) là tập đối xứng do đó \(\forall x \in D \Rightarrow - x \in D\left( * \right)\)

Đặt \(y = f\left( x \right) = 2x.\sin x\)

Với \(\forall x \in D\) ta có:

\(f\left( { - x} \right) = 2\left( { - x} \right).\sin \left( { - x} \right) = 2x.\sin x = f\left( x \right)\left( {**} \right)\)

Từ (*) và (**) suy ra hàm số đã cho là hàm số chẵn.

b) Tập xác định \(D = \mathbb{R}\) là tập đối xứng

Đặt \(y = f\left( x \right) = \cos x + \sin 2x\)

Xét \(x = \frac{\pi }{3} \in D \Rightarrow x = - \frac{\pi }{3} \in D\)

\(\begin{matrix} f\left( {\dfrac{\pi }{3}} \right) = \cos \left( {\dfrac{\pi }{3}} \right) + \sin \left( {\dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2} \hfill \\ f\left( { - \dfrac{\pi }{3}} \right) = \cos \left( { - \dfrac{\pi }{3}} \right) + \sin \left( { - \dfrac{{2\pi }}{3}} \right) = \dfrac{1}{2} - \dfrac{{\sqrt 3 }}{2} \hfill \\ \end{matrix}\)

Ta thấy \(f\left( {\frac{\pi }{3}} \right) \ne f\left( { - \frac{\pi }{3}} \right)\) nên hàm số đã cho không là hàm số chẵn.

\(f\left( {\frac{\pi }{3}} \right) \ne - f\left( { - \frac{\pi }{3}} \right)\) nên hàm số đã cho không là hàm số lẻ.

Vậy hàm số đã cho không chẵn, không lẻ.

c) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\) là tập đối xứng do đó \(\forall x \in D \Rightarrow - x \in D\left( * \right)\)

Đặt \(f\left( x \right) = \frac{{\cos 2x}}{x}\)

Với \(\forall x \in D\) ta có:

.\(f\left( { - x} \right) = \frac{{\cos \left( { - 2x} \right)}}{{ - x}} = - \frac{{\cos \left( {2x} \right)}}{x} = - f\left( x \right)\left( {**} \right)\)

Từ (*) và (**) suy ra hàm số đã cho là hàm số lẻ.

b) Hàm số tuần hoàn

Ví dụ: Xét tính tuần hoàn và chu kì cơ sở của các hàm số sau:

a. \(y = 1 - \sin 5x\)	b. \(y = {\cos ^2}x - 1\)
c. \(y = \sin \left( {\frac{{2x}}{5}} \right).\cos \left( {\frac{{2x}}{5}} \right)\)	d. \(y = \cos x + \cos \left( {\sqrt 3 x} \right)\)

Hướng dẫn giải

a) Hàm số \(y = 1 - \sin 5x\) tuần hoàn với chu kì \(T = \frac{{2\pi }}{5}\)

b) Hàm số \(y = {\cos ^2}x - 1 = \frac{{\cos 2x - 1}}{2}\) tuần hoàn với chu kì \(T = \pi\)

a) Ta có: \(y = \sin \left( {\frac{{2x}}{5}} \right).\cos \left( {\frac{{2x}}{5}} \right) = \frac{1}{2}\sin \left( {\frac{{4x}}{5}} \right)\)

Hàm số tuần hoàn với chu kì

d) Hàm số \(y = \cos x + \cos \left( {\sqrt 3 x} \right)\) không tuần hoàn.

Vì ta có hàm số \(y = \cos x\) tuần hoàn với chu kì \({T_1} = 2\pi\) và hàm số \(y = \cos \left( {\sqrt 3 x} \right)\) tuần hoàn với chu kì \({T_2} = \frac{{2\pi }}{{\sqrt 3 }}\) nhưng không tồn tại bội chung nhỏ nhất của \({T_1} = 2\pi\) và \({T_2} = \frac{{2\pi }}{{\sqrt 3 }}\).

3. Đồ thị của các hàm số lượng giác

a) Hàm số y = sinx

- Tập xác định: \(D = \mathbb{R}\)

- Tập giá trị [-1; 1] hay \(- 1 \leqslant \operatorname{sinx} \leqslant 1,\forall x \in \mathbb{R}\)

- Hàm số là hàm số lẻ tuần hoàn với chu kì \(T = 2\pi\)

- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\), \(k \in \mathbb{Z}\)

- Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.

Đồ thị hàm số \(y = \sin x\)

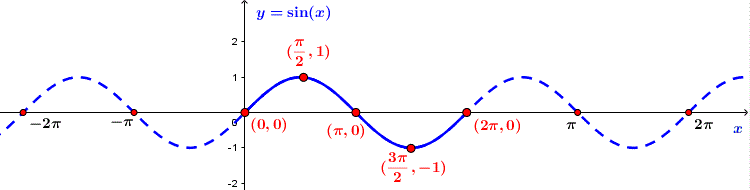
b) Hàm số y = cosx

- Tập xác định: \(D = \mathbb{R}\)

- Tập giá trị [-1; 1] hay \(- 1 \leqslant \operatorname{cosx} \leqslant 1,\forall x \in \mathbb{R}\)

- Hàm số là hàm chẵn tuần hoàn với chu kì \(T = 2\pi\)

- Đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\), \(k \in \mathbb{Z}\)

- Có đồ thị là một đường hình sin đối xứng qua trục tung.

Đồ thị hàm số \(y = \cos x\)

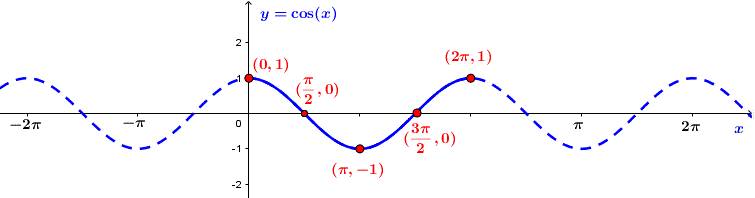
c) Hàm số y = tanx

- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)

- Tập giá trị: \(\mathbb{R}\)

- Hàm số là hàm lẻ tuần hoàn với chu kì \(T = \pi\)

- Đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\)

- Có đồ thị đối xứng qua gốc tọa độ.

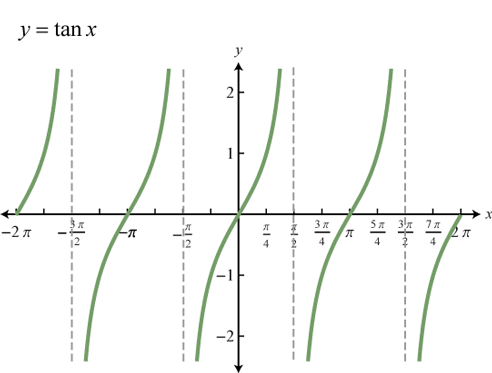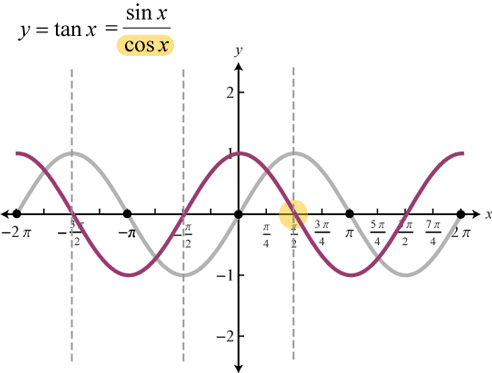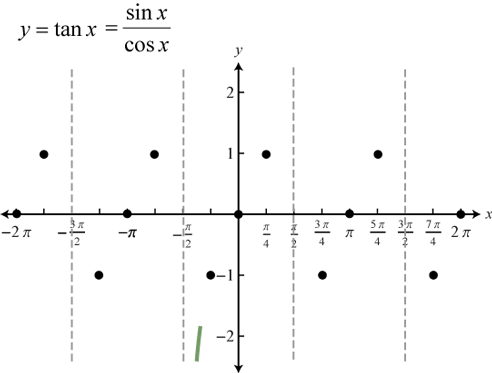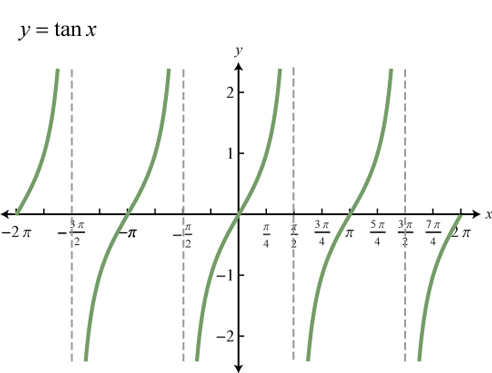
Đồ thị hàm số \(y = \tan x\)

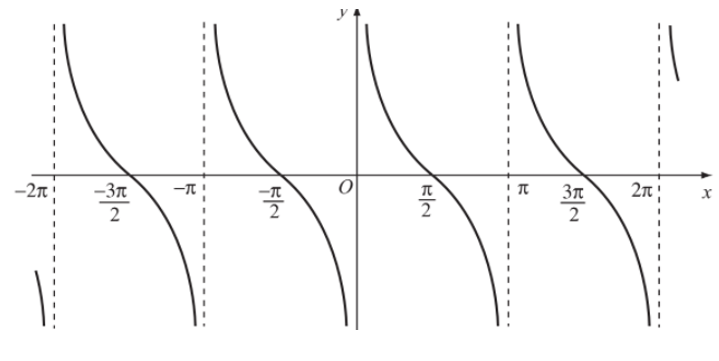
d) Hàm số y = cotx

- Tập xác định: \(D = \mathbb{R}\backslash \left\{ {k\pi ,k \in \mathbb{Z}} \right\}\)

- Tập giá trị: \(\mathbb{R}\)

- Hàm số là hàm lẻ tuần hoàn với chu kì \(T = \pi\)

- Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in \mathbb{Z}\)

- Có đồ thị đối xứng qua gốc tọa độ.

Đồ thị hàm số \(y = \cot x\)