Đường thẳng và mặt phẳng song song CTST
Cho đường thẳng 
\(d\) và mặt phẳng \((P)\):
|
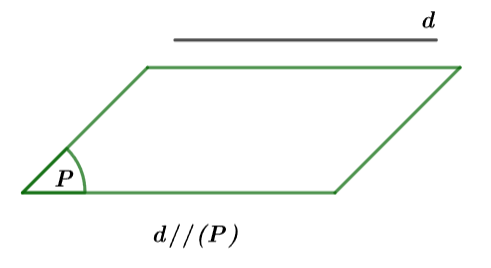
Trường hợp 1: Nếu
|
Hình vẽ minh họa
|
|
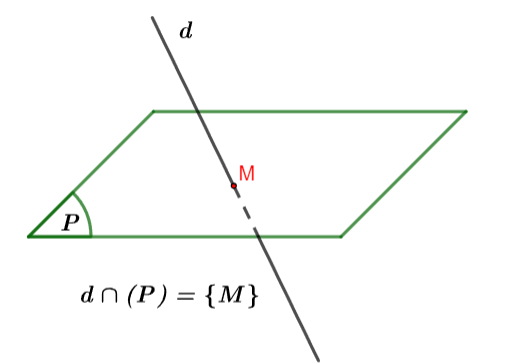
Trường hợp 2: Nếu
|
Hình vẽ minh họa
|
|
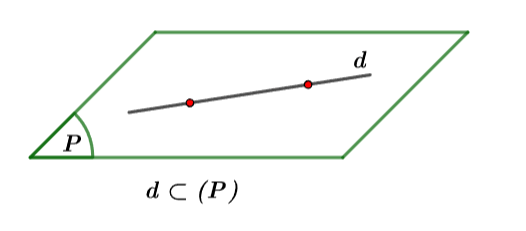
Trường hợp 3: Nếu
|
Hình vẽ minh họa
|
Đường thẳng \(d\) song song với mặt phẳng \((P)\) nếu chúng không có điểm chung.
2. Điều kiện để một đường thẳng song song với một mặt phẳng
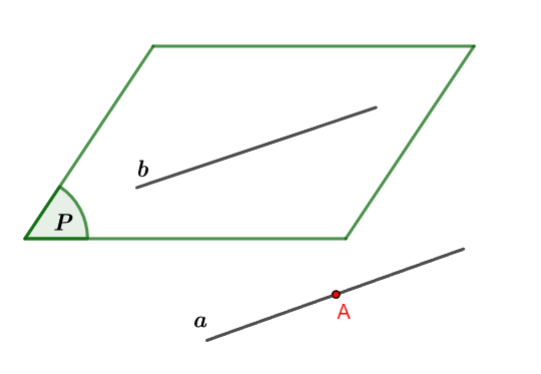
Định lí 1: Nếu đường thẳng \(a\) không nằm trong mặt phẳng \((P)\) và song song với đường thẳng \(b\) nào đó nằm trong \((P)\) thì \(a\) song song với \((P)\).
Hình vẽ minh họa
3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
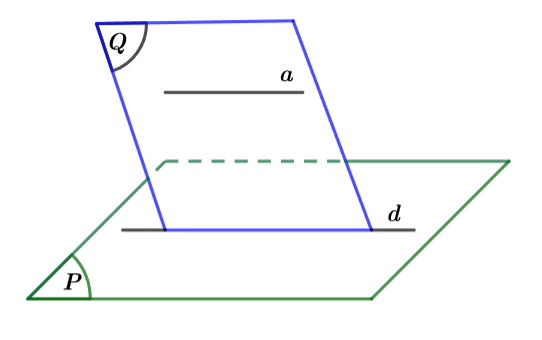
Định lí 2: Cho đường thẳng \(a\) song song với mặt phẳng \((P)\). Nếu mặt phẳng (Q) chứa \(a\), cắt \((P)\) theo giao tuyến \(d\) thì \(a\) song song với \(d\).
Hệ quả 1: Cho đường thẳng \(a\) song song với mặt phẳng \((P)\). Nếu qua điểm M thuộc \((P)\) ta vẽ đường thẳng \(b\) song song với \(a\) thì \(b\) phải nằm trong \((P)\).
Hệ quả 2: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Ví dụ: Cho tứ diện \(ABCD\). Giả sử \(G_1, G_2\) lần lượt là trọng tâm tam giác \(ABD\) và \(ACD\). Tìm giao tuyến của hai mặt phẳng \((AG_1G_2)\) với mặt phẳng \((ABC)\).
Hướng dẫn giải
Hình vẽ minh họa
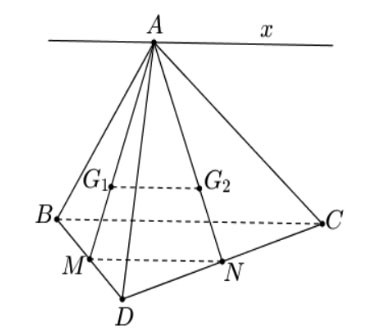
Gọi M và N theo thứ tự là trung điểm của BD và CD.
Trong tam giác \(ΔAMN\), ta có:
\(\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}} = \frac{2}{3}\)\(\Rightarrow {G_1}{G_2}//MN\)
Do \(MN//BC;{G_1}{G_2}//MN\)
Mà \(\left\{ \begin{gathered}
A \in \left( {A{G_1}{G_2}} \right) \cap \left( {ABC} \right) \hfill \\
{G_1}{G_2}//BC \hfill \\
\end{gathered} \right.\)
\(\Rightarrow \left( {A{G_1}{G_2}} \right) \cap \left( {ABC} \right) = Ax//{G_1}{G_2}//BC\)
Định lí 3: Nếu \(a\) và \(b\) là hai đường thẳng chéo nhau thì qua \(a\), có một và chỉ một mặt phẳng song song với \(b\).
Hình vẽ minh họa
Ví dụ: Cho tứ diện \(ABCD\). Giả sử \(M\) thuộc đoạn thẳng \(BC\). Xác định thiết diện của tứ diện \(ABCD\) cắt bởi mặt phẳng \((α)\) qua \(M\) song song với \(AB\) và \(CD\).
Hướng dẫn giải
Hình vẽ minh họa
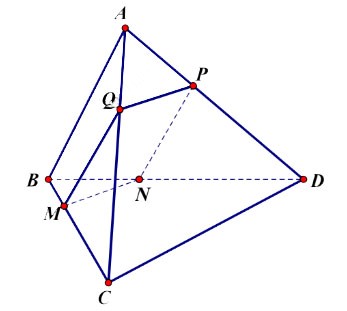
Ta có:
\((α) // AB\) nên giao tuyến của \((α)\) với (ABC) là đường thẳng đi qua M và song song với AB và
cắt AC tại Q.
\((α) // CD\) nên giao tuyến của \((α)\) với (BCD) là đường thẳng đi qua M và song song với CD và
cắt BD tại N.
\((α) // AB\) nên giao tuyến của \((α)\) với (ABD) là đường thẳng đi qua N và song song với AB và
cắt AD tại P.
Ta có \(MN // PQ // CD // MQ // PN // AB\)
Vậy thiết diện là hình bình hành \(MNPQ\).
