Biến cố giao và quy tắc nhân xác suất CTST
Cho hai biến cố 
\(A\) và \(B\). Biến cố “Cả \(A\) và \(B\) cùng xảy ra”, kí hiệu \(AB\) hoặc \(A∩B\) được gọi là biến cố giao của \(A\) và \(B\).
Hình vẽ minh họa
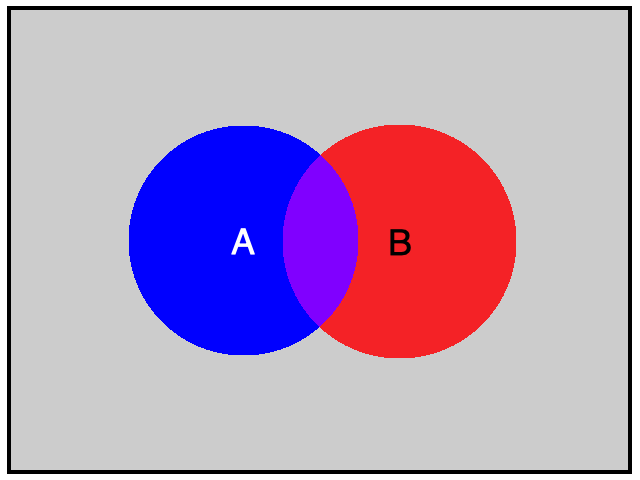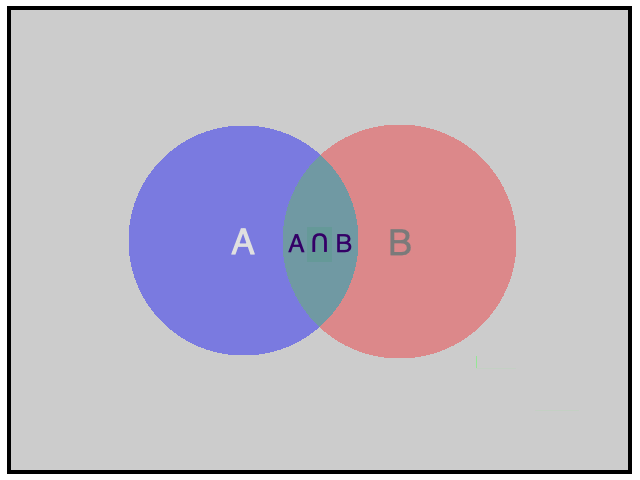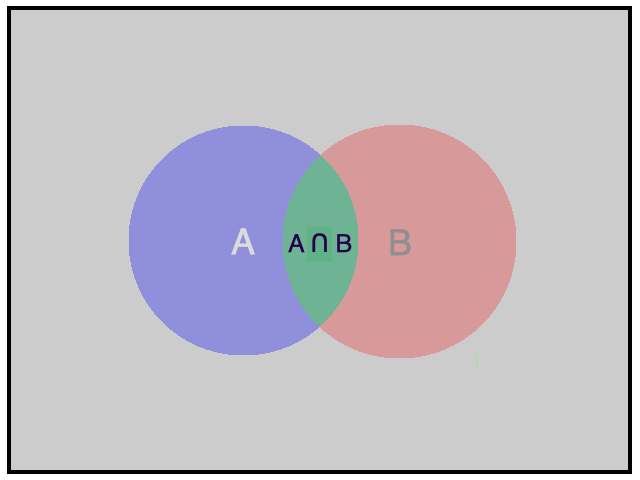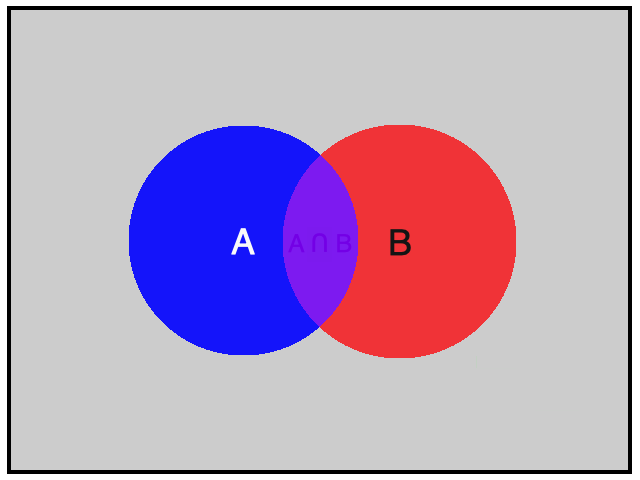
Chú ý: Tập hợp mô tả biến cố \(AB\) là giao của hai tập hợp mô tả biến cố \(A\) và biến cố \(B\). Biến cố AB xảy ra khi và chỉ khi cả hai biến cố \(A\) và \(B\) xảy ra.
Ví dụ: Xét phép thử gieo ngẫu nhiên một con xúc xắc đồng chất sáu mặt. Gọi là biến cố: "Số chấm thu được là số chẵn" và C là biến cố: "Số chấm thu được là số nhỏ hơn 4". Hãy mô tả biến cố giao AC.
Hướng dẫn giải
Ta có: \(A= \left \{2;4;6 \right \} , C=\left \{ 1;2;3 \right \}\).
Suy ra: \(A∩C=\left \{ 2 \right \}\).
2. Hai biến cố xung khắc
Hai biến cố \(A\) và \(B\) được gọi là xung khắc nếu \(A\) và \(B\) không đồng thời xảy ra.
Chú ý: Hai biến cố \(A\) và \(B\) là xung khắc khi và chỉ khi \(A∩B= ∅\).
Ví dụ: Xét phép thử gieo ngẫu nhiên một con xúc xắc đồng chất sáu mặt. Gọi A là biến cố: "Số chấm thu được là số nhỏ hơn 3 ", B là biến cố: "Số chấm thu được là số lớn hơn hoặc bằng 4 " và C là biến cố: "Số chấm thu được là số lẻ”. Có bao nhiêu cặp biến cố xung khắc?
Hướng dẫn giải
Ta có: \(A=\left \{ 1;2 \right \} , B= \left \{ 4;5;6\right \} , C=\left \{ 1;3;5 \right \}\)
Ta thấy A và B là các biến cố xung khắc vì nếu A xảy ra thì B không thể xảy ra và ngược lại (hay \(A∩B= ∅\)).
Vì \(A∩C=\left \{ 1 \right \} ≠∅, B∩C=\left \{ 5 \right \} ≠∅\) nên các cặp biến cố A,C và B,C không phải là biến cố xung khắc.
3. Biến cố độc lập
Hai biến cố A và \(B\) được gọi là độc lập nếu việc xảy ra hay không xảy ra của biến cố này không làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Nhận xét: Nếu hai biến cố \(A\) và \(B\) độc lập thì các cặp biến cố \(\left\{ \begin{gathered}
\overline A ;B \hfill \\
A;\overline B \hfill \\
\overline A ;\overline B \hfill \\
\end{gathered} \right.\) cùng độc lập.
4. Quy tắc nhân xác suất của hai biến cố độc lập
Nếu hai biến cố \(A\) và \(B\) độc lập thì \(P\left( {AB} \right) = P\left( A \right).P\left( B \right)\).
Chú ý: Từ quy tắc nhân xác suất ta thấy nếu \(P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\) thì hai biến cố \(A\) và \(B\) không độc lập.
Ví dụ: Gieo hai đồng xu cân đối. Xét các biến cố A: "Cả hai đồng xu đều ra mặt sấp", B: "Có ít nhất một đồng xu ra mặt sấp". Hỏi A và B có độc lập hay không?
Hướng dẫn giải
Ta có: \(\Omega = \left\{ {SS;SN;NS;NN} \right\} \Rightarrow n\left( \Omega \right) = 4\)
Ta có:
\(A = \left\{ {SS} \right\} \Rightarrow n\left( A \right) = 1 \Rightarrow P\left( A \right) = \frac{1}{4}\)
\(B = \left\{ {SS;SN;NS} \right\} \Rightarrow n\left( B \right) = 3 \Rightarrow P\left( B \right) = \frac{3}{4}\)
\(AB = A \cap B = \left\{ {SS} \right\} \Rightarrow n\left( {A \cap B} \right) = 1\)
\(\Rightarrow P\left( {AB} \right) = \frac{1}{4}\)
Ta có: \(P\left( {AB} \right) = \frac{4}{{16}} \ne P\left( A \right).P\left( B \right) = \frac{1}{4}.\frac{3}{4} = \frac{3}{{16}}\)
Vậy hai biến cố A và B không độc lập.
