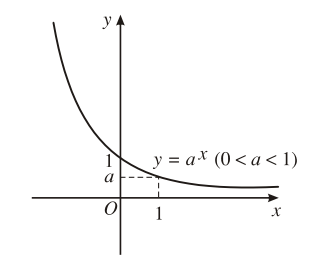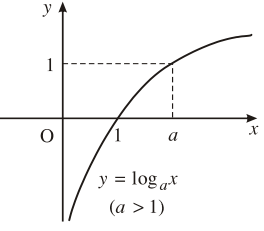Hàm số mũ. Hàm số lôgarit CTST
Định nghĩa hàm số mũ
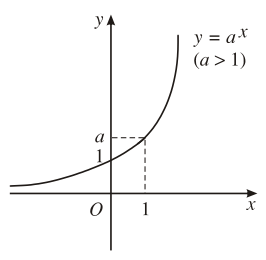
Cho số thực dương 
\(a \ne 1\). Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
Đặc điểm của hàm số mũ
|
|
|
|
| 1. Tập xác định |
\(\mathbb{R}\) |
\(\mathbb{R}\) |
| 2. Sự biến thiên | Đồng biến trên \(\mathbb{R}\) |
Nghịch biến trên \(\mathbb{R}\) |
| 3. Sự liên tục | \(\mathbb{R}\) |
\(\mathbb{R}\) |
| 4. Giới hạn đặc biệt | \(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = 0 \hfill \\
\mathop {\lim }\limits_{x \to + \infty } a = + \infty \hfill \\
\end{matrix}\) |
\(\begin{matrix}
\mathop {\lim }\limits_{x \to - \infty } {a^x} = + \infty \hfill \\
\mathop {\lim }\limits_{x \to + \infty } {a^x} = 0 \hfill \\
\end{matrix}\) |
|
5. Đồ thị hàm số |
Đồ thị luôn đi qua các điểm |
Đồ thị luôn đi qua các điểm |
Ví dụ: So sánh các cặp số sau:
a) \(0,{75^{ - 0,1}}\) và \(0,{75^{ - 0,2}}\)
b) \(\sqrt[4]{4}\) và \(\sqrt[5]{8}\)
Hướng dẫn giải
a) Do \(0,75 < 1\) nên hàm số \(y = 0,{75^x}\) nghịch biến trên \(\mathbb{R}\) và \(- 0,1 > - 0,2\) nên \(0,{75^{ - 0,1}} < 0,{75^{ - 0,2}}\).
b) Ta có: \(\sqrt[4]{4} = {2^{\frac{2}{3}}};\sqrt[5]{8} = {2^{\frac{3}{5}}}\)
Do \(2 > 1\) nên hàm số \(y = {2^x}\) đồng biến trên \(\mathbb{R}\) và \(\frac{2}{3} > \frac{3}{5}\) nên \({2^{\frac{2}{3}}} > {2^{\frac{3}{5}}}\) hay \(\sqrt[4]{4} > \sqrt[5]{8}\)
Ví dụ: Dựa vào đồ thị hàm số, cho biết với giá trị nào của x thì đồ thị hàm số \(y = {3^x}\):
a) Nằm ở phía trên đường thẳng \(y=3\)
b) Nằm ở phía dưới đường thẳng \(y=1\)
Hướng dẫn giải
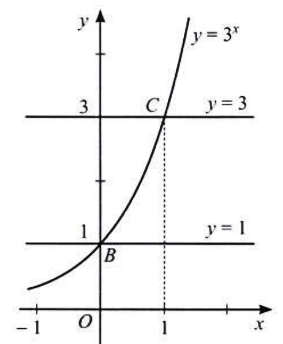
a) Đường thẳng \(y=3\) cắt đồ thị hàm số \(y = {3^x}\) tại điểm \(C(1; 3)\)
Dựa vào hình vẽ ta thấy đồ thị hàm số \(y = {3^x}\) nằm phía trên đường thẳng \(y=3\) khi .
b) Đường thẳng \(y=1\) cắt đồ thị hàm số \(y = {3^x}\) tại điểm
Dựa vào hình vẽ ta thấy đồ thị hàm số \(y = {3^x}\) nằm phía dưới đường thẳng \(y=1\) khi x < 0.
2. Hàm số lôgarit
Định nghĩa hàm số lôgarit
Cho \(a\) là số thực dương và \(a \ne 1\).
Hàm số \(y = \log_{a}x\) được gọi là hàm số lôgarit cơ số \(a\).
Đặc điểm của hàm số lôgarit
|
|
|
|
| 1. Tập xác định |
|
\((0; + \infty )\) |
| 2. Sự biến thiên | Đồng biến trên \((0; + \infty )\) |
Nghịch biến trên \((0; + \infty )\) |
| 3. Sự liên tục | \(\mathbb{R}\) |
\(\mathbb{R}\) |
| 4. Giới hạn đặc biệt |
|
|
|
5. Đồ thị hàm số |
Đi qua các điểm |
Đi qua các điểm |
Ví dụ: Tìm tất cả các giá trị của tham số m để hàm số \(y = {\log _3}\left( {4{x^2} - 4x + m} \right)\) xác định trên \(\mathbb{R}\).
Hướng dẫn giải
Hàm số \(y = {\log _3}\left( {4{x^2} - 4x + m} \right)\) xác định trên \(\mathbb{R}\) khi và chỉ khi
\(4{x^2} - 4x + m > 0\forall x \in \mathbb{R}\) \(\Leftrightarrow \Delta < 0 \Leftrightarrow m > 1\)
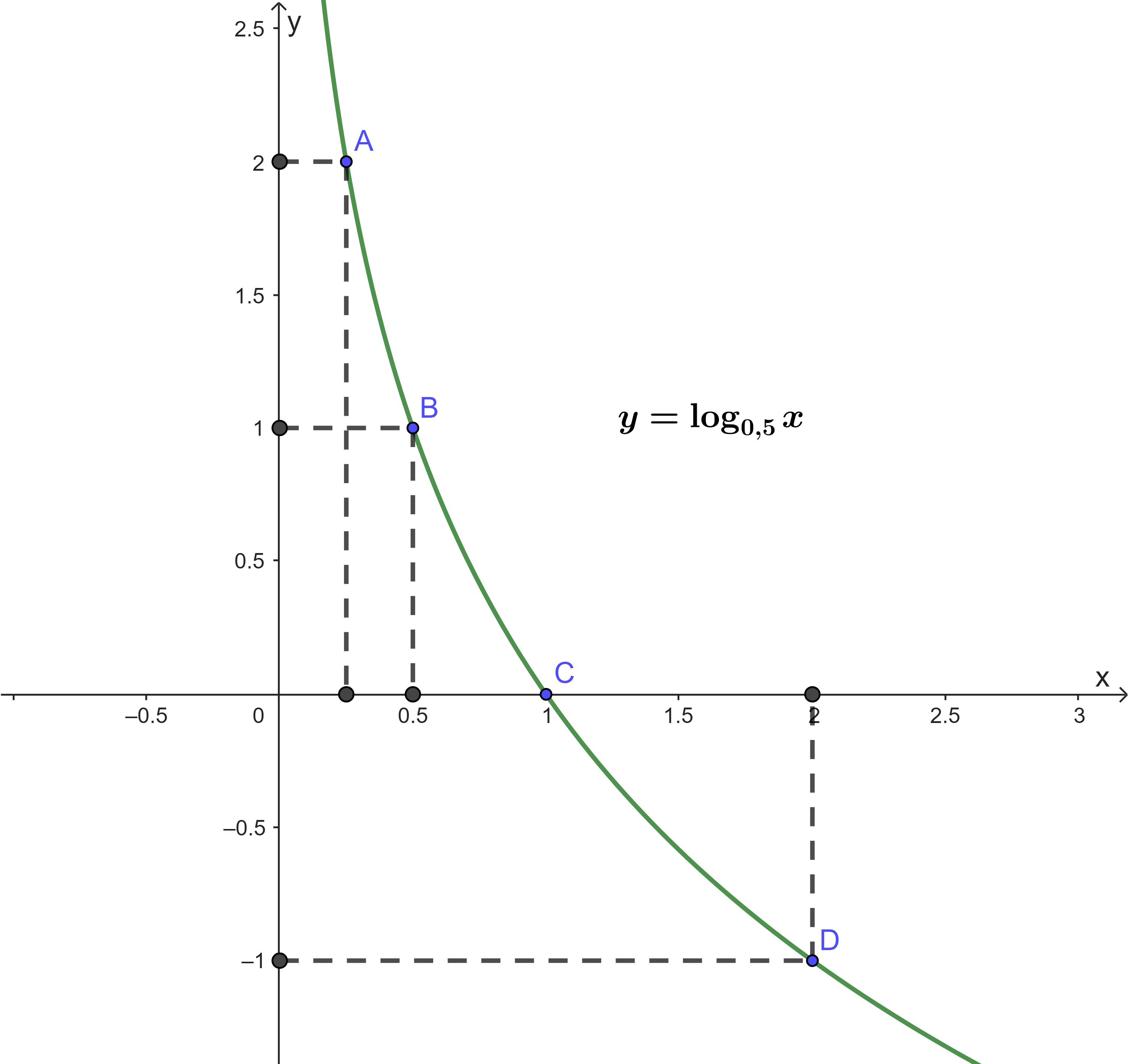
Ví dụ: Vẽ đồ thị hàm số \(y = {\log _{0,5}}x\).
Hướng dẫn giải
Tập xác định \(\left( {0; + \infty } \right)\)
Do \(0 < 0,5 < 1\) nên hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Bảng giá trị:
|
x |
0,25 |
0,5 |
1 |
2 |
4 |
|
y |
2 |
1 |
0 |
-1 |
-2 |
Đồ thị hàm số đi qua các điểm có toạ độ theo bảng giá trị và nằm bên phải trục tung.
Từ đó, ta vẽ được đồ thị hàm số như hình bên:
