Phương trình, bất phương trình mũ và lôgarit CTST
Phương trình mũ cơ bản có dạng
![]() \({a^x} = b{\text{ }}\left( {a > 0,{\text{ }}a \ne 1} \right)\)
\({a^x} = b{\text{ }}\left( {a > 0,{\text{ }}a \ne 1} \right)\)
Để giải phương trình mũ, ta xét hai trường hợp sau:
- Khi
 \(b > 0\) phương trình có một nghiệm duy nhất.
\(b > 0\) phương trình có một nghiệm duy nhất. - Khi
 \(b \leq 0\) phương trình vô nghiệm.
\(b \leq 0\) phương trình vô nghiệm.
Minh họa bằng đồ thị
|
|
|
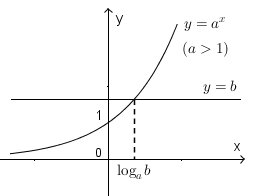 |
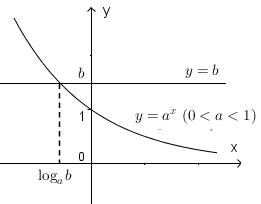 |
Cách giải phương trình mũ
![]() \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow a = 1\) hoặc
\({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow a = 1\) hoặc ![]() \(\left\{ \begin{gathered}
0 < a \ne 1 \hfill \\
f\left( x \right) = g\left( x \right) \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{gathered}
0 < a \ne 1 \hfill \\
f\left( x \right) = g\left( x \right) \hfill \\
\end{gathered} \right.\)
Ví dụ: Giả sử ![]() \(x_{1};x_{2}\) là hai nghiệm của phương trình
\(x_{1};x_{2}\) là hai nghiệm của phương trình ![]() \(2^{x^{2} - x + 8} - 4^{1 - 3x} =
0\) . Xác định giá trị biểu thức
\(2^{x^{2} - x + 8} - 4^{1 - 3x} =
0\) . Xác định giá trị biểu thức ![]() \(M =
4{x_{1}}^{2} - {x_{2}}^{2}\) biết
\(M =
4{x_{1}}^{2} - {x_{2}}^{2}\) biết ![]() \(x_{1} > x_{2}\) ?
\(x_{1} > x_{2}\) ?
Hướng dẫn giải
Ta có:
![]() \(2^{x^{2} - x + 8} - 4^{1 - 3x} = 0
\Leftrightarrow 2^{x^{2} - x + 8} = \left( 2^{2} ight)^{1 -
3x}\)
\(2^{x^{2} - x + 8} - 4^{1 - 3x} = 0
\Leftrightarrow 2^{x^{2} - x + 8} = \left( 2^{2} ight)^{1 -
3x}\)
![]() \(\Leftrightarrow 2^{x^{2} - x + 8} =
2^{2.(1 - 3x)}\)
\(\Leftrightarrow 2^{x^{2} - x + 8} =
2^{2.(1 - 3x)}\)
![]() \(\Leftrightarrow x^{2} - x + 8 = 2.(1 -
3x)\)
\(\Leftrightarrow x^{2} - x + 8 = 2.(1 -
3x)\)
![]() \(\Leftrightarrow x^{2} + 5x + 6 = 0
\Leftrightarrow \left\lbrack \begin{matrix}
x_{1} = - 2 \\
x_{2} = - 3 \\
\end{matrix} ight.\ (tm)\)
\(\Leftrightarrow x^{2} + 5x + 6 = 0
\Leftrightarrow \left\lbrack \begin{matrix}
x_{1} = - 2 \\
x_{2} = - 3 \\
\end{matrix} ight.\ (tm)\)
![]() \(\Rightarrow M = 4{x_{1}}^{2} -
{x_{2}}^{2} = 7\)
\(\Rightarrow M = 4{x_{1}}^{2} -
{x_{2}}^{2} = 7\)
2. Phương trình lôgarit
Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
Phương trình lôgarit cơ bản có dạng:
![]() \({\log _a}f(x) = b\)
\({\log _a}f(x) = b\) ![]() \((a > 0,\,\,a \ne 1 )\)
\((a > 0,\,\,a \ne 1 )\)
Để giải phương trình lôgarit cơ bản, ta có:
![]() \({\log _a}f(x) = b \Leftrightarrow x =a^b\)
\({\log _a}f(x) = b \Leftrightarrow x =a^b\)
Minh họa bằng đồ thị
|
|
|
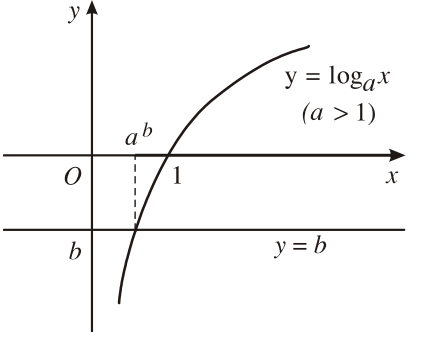 |
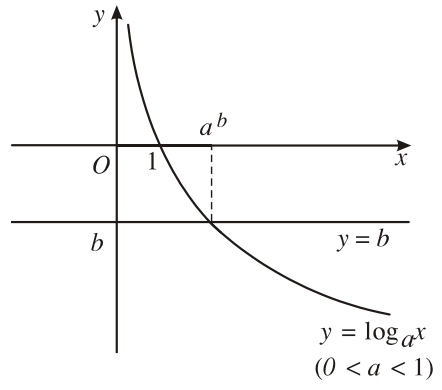 |
|
|
|
Cách giải phương trình lôgarit
![]() \({\log _a}f(x) = {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) = g(x) \hfill \\
\end{gathered} \right.\) , với mọi
\({\log _a}f(x) = {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) = g(x) \hfill \\
\end{gathered} \right.\) , với mọi ![]() \(0 < a \ne 1\)
\(0 < a \ne 1\)
Ví dụ: Giả sử ![]() \(S\) là tổng các nghiệm của phương trình:
\(S\) là tổng các nghiệm của phương trình:
![]() \(\frac{1}{4}\log_{4}(a - 3)^{8} +\frac{1}{2}\log_{\sqrt{2}}(a + 1) = \log_{2}(4a)\)
\(\frac{1}{4}\log_{4}(a - 3)^{8} +\frac{1}{2}\log_{\sqrt{2}}(a + 1) = \log_{2}(4a)\)
Giá trị của ![]() \(S\) bằng bao nhiêu?
\(S\) bằng bao nhiêu?
Hướng dẫn giải
Điều kiện xác định  \(\left\{ \begin{matrix}
(a - 3)^{8} > 0 \\
a + 1 > 0 \\
4a > 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}
a eq 3 \\
a > - 1 \\
a > 0 \\
\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}
a eq 3 \\
a > 0 \\
\end{matrix} ight.\)
\(\left\{ \begin{matrix}
(a - 3)^{8} > 0 \\
a + 1 > 0 \\
4a > 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}
a eq 3 \\
a > - 1 \\
a > 0 \\
\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}
a eq 3 \\
a > 0 \\
\end{matrix} ight.\)
Phương trình đã cho tương đương:
![]() \(\Leftrightarrow \dfrac{1}{4}\log_{2^{2}}(a- 3)^{8} + \frac{1}{2}\log_{2^{\frac{1}{2}}}(a + 1) =\log_{2}(4a)\)
\(\Leftrightarrow \dfrac{1}{4}\log_{2^{2}}(a- 3)^{8} + \frac{1}{2}\log_{2^{\frac{1}{2}}}(a + 1) =\log_{2}(4a)\)
![]() \(\Leftrightarrow \log_{2}|a - 3| +\log_{2}(a + 1) = \log_{2}(4a)\)
\(\Leftrightarrow \log_{2}|a - 3| +\log_{2}(a + 1) = \log_{2}(4a)\)
![]() \(\Leftrightarrow \log_{2}|a - 3| =\log_{2}(4a) - \log_{2}(a + 1)\)
\(\Leftrightarrow \log_{2}|a - 3| =\log_{2}(4a) - \log_{2}(a + 1)\)
![]() \(\Leftrightarrow \log_{2}|a - 3| =\log_{2}\left( \frac{4a}{a + 1} ight)\)
\(\Leftrightarrow \log_{2}|a - 3| =\log_{2}\left( \frac{4a}{a + 1} ight)\)
 \(\Leftrightarrow |a - 3| = \dfrac{4a}{a +1} \Leftrightarrow \left\lbrack \begin{matrix}a - 3 = \dfrac{4a}{a + 1} \\a - 3 = - \dfrac{4a}{a + 1} \\\end{matrix} ight.\)
\(\Leftrightarrow |a - 3| = \dfrac{4a}{a +1} \Leftrightarrow \left\lbrack \begin{matrix}a - 3 = \dfrac{4a}{a + 1} \\a - 3 = - \dfrac{4a}{a + 1} \\\end{matrix} ight.\)
 \(\Leftrightarrow \left\lbrack
\begin{matrix}
a^{2} - 6a - 3 = 0 \\
a^{2} + 2a - 3 = 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}
a = 3 + 2\sqrt{3}(tm) \\
a = 3 - 2\sqrt{3}(ktm) \\
a = 1(tm) \\
a = - 3(ktm) \\
\end{matrix} ight.\)
\(\Leftrightarrow \left\lbrack
\begin{matrix}
a^{2} - 6a - 3 = 0 \\
a^{2} + 2a - 3 = 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix}
a = 3 + 2\sqrt{3}(tm) \\
a = 3 - 2\sqrt{3}(ktm) \\
a = 1(tm) \\
a = - 3(ktm) \\
\end{matrix} ight.\)
![]() \(\Rightarrow S = 3 + 2\sqrt{3} + 1 = 4 +
2\sqrt{3}\)
\(\Rightarrow S = 3 + 2\sqrt{3} + 1 = 4 +
2\sqrt{3}\)
3. Bất phương trình mũ
a) Định nghĩa bất phương trình mũ
Bất phương trình mũ cơ bản có dạng ![]() \({a^x} > b\) (hoặc
\({a^x} > b\) (hoặc ![]() \({a^x} \geqslant b,{a^x} < b,{a^x} \leqslant b\)) với
\({a^x} \geqslant b,{a^x} < b,{a^x} \leqslant b\)) với ![]() \(a > 0,a \ne 1\).
\(a > 0,a \ne 1\).
Để giải, ta xét bất phương trình có dạng ![]() \({a^x} > b\)
\({a^x} > b\)
- Nếu
 \(b \leq 0\), tập nghiệm của bất phương trình là
\(b \leq 0\), tập nghiệm của bất phương trình là  \(\mathbb{R}\), vì
\(\mathbb{R}\), vì  \({a^x} > b,\forall x \in \mathbb{R}\)
\({a^x} > b,\forall x \in \mathbb{R}\) - Nếu
 \(b > 0\) thì bất phương trình tương đương với
\(b > 0\) thì bất phương trình tương đương với  \({a^x} > {a^{{{\log }_a}b}}\), khi đó:
\({a^x} > {a^{{{\log }_a}b}}\), khi đó:
-
- Với
 \(a>1\), nghiệm của bất phương trình là
\(a>1\), nghiệm của bất phương trình là  \(x > {\log _a}b\)
\(x > {\log _a}b\) - Với
 \(0 < a < 1\), nghiệm của bất phương trình là
\(0 < a < 1\), nghiệm của bất phương trình là  \(x < {\log _a}b\)
\(x < {\log _a}b\)
- Với
b) Cách giải bất phương trình mũ
- Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
 \(\boxed{{a^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
a > 1 \hfill \\
f\left( x \right) > g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
0 < a < 1 \hfill \\
f\left( x \right) < g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.}\)
\(\boxed{{a^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
a > 1 \hfill \\
f\left( x \right) > g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
0 < a < 1 \hfill \\
f\left( x \right) < g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.}\)
- Tương tự với bất phương trình dạng:
 \(\left[ \begin{gathered}
{a^{f\left( x \right)}} \geqslant {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} < {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} \leqslant {a^{g\left( x \right)}} \hfill \\
\end{gathered} \right.\)
\(\left[ \begin{gathered}
{a^{f\left( x \right)}} \geqslant {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} < {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} \leqslant {a^{g\left( x \right)}} \hfill \\
\end{gathered} \right.\)
- Trong trường hợp cơ số
 \(a\) có chứa ẩn số thì:
\(a\) có chứa ẩn số thì:
![]() \(\boxed{{a^M} > {a^N} \Leftrightarrow \left( {a - 1} \right)\left( {M - N} \right) > 0}\).
\(\boxed{{a^M} > {a^N} \Leftrightarrow \left( {a - 1} \right)\left( {M - N} \right) > 0}\).
- Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ: đưa về cùng cơ số; đặt ẩn phụ.
Ví dụ: Cho bất phương trình ![]() \(\left( \frac{1}{3} ight)^{x} > 9\) . Xác định nghiệm của bất phương trình đã cho?
\(\left( \frac{1}{3} ight)^{x} > 9\) . Xác định nghiệm của bất phương trình đã cho?
Hướng dẫn giải
Ta có:
![]() \(\left( \frac{1}{3} ight)^{x} > 9\Leftrightarrow \left( 3^{- 1} ight)^{x} > 3^{2}\)
\(\left( \frac{1}{3} ight)^{x} > 9\Leftrightarrow \left( 3^{- 1} ight)^{x} > 3^{2}\)
![]() \(\Leftrightarrow 3^{- x} > 3^{2}\Leftrightarrow x < - 2\)
\(\Leftrightarrow 3^{- x} > 3^{2}\Leftrightarrow x < - 2\)
Vậy tập nghiệm của bất phương trình là ![]() \(x\in ( - \infty; - 2)\)
\(x\in ( - \infty; - 2)\)
4. Bất phương trình lôgarit
a) Định nghĩa bất phương trình lôgarit
Bất phương trình lôgarit là bất phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit.
Bất phương trình logarit cơ bản có dạng ![]() \({\log _a}x > b\) (hoặc
\({\log _a}x > b\) (hoặc ![]() \({\log _a}x \geqslant b,\)
\({\log _a}x \geqslant b,\)![]() \({\log _a}x < b,\)
\({\log _a}x < b,\)![]() \({\log _a}x \leqslant b\)) với
\({\log _a}x \leqslant b\)) với ![]() \(a > 0,a \ne 1\).
\(a > 0,a \ne 1\).
Để giải, ta xét bất phương trình ![]() \({\log _a}x > b\) như sau:
\({\log _a}x > b\) như sau:
- Trường hợp
 \(a>1\), ta có:
\(a>1\), ta có:  \({\log _a}x > b \Leftrightarrow x > {a^b}\)
\({\log _a}x > b \Leftrightarrow x > {a^b}\)- Trường hợp
 \(0 < a < 1\), ta có:
\(0 < a < 1\), ta có:
![]() \({\log _a}x > b \Leftrightarrow 0 < x < {a^b}\)
\({\log _a}x > b \Leftrightarrow 0 < x < {a^b}\)
b) Cách giải bất phương trình lôgarit
Nếu ![]() \(a> 1\) thì
\(a> 1\) thì
![]() \({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
g(x) > 0 \hfill \\
f(x) > g(x) \hfill \\
\end{gathered} \right.\)
\({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
g(x) > 0 \hfill \\
f(x) > g(x) \hfill \\
\end{gathered} \right.\)
Nếu ![]() \(0 < a < 1\) thì
\(0 < a < 1\) thì
![]() \({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) < g(x) \hfill \\
\end{gathered} \right.\)
\({\log _a}f(x) > {\log _a}g(x) \Leftrightarrow \left\{ \begin{gathered}
f(x) > 0 \hfill \\
f(x) < g(x) \hfill \\
\end{gathered} \right.\)
Ví dụ: Tìm giá trị tham số m để bất phương trình ![]() \(1 + \log_{5}\left( x^{2} + 1 ight) \geq \log_{5}\left( mx^{2} + 4x + m ight)\) có nghiệm đúng với mọi x.
\(1 + \log_{5}\left( x^{2} + 1 ight) \geq \log_{5}\left( mx^{2} + 4x + m ight)\) có nghiệm đúng với mọi x.
Hướng dẫn giải
Ta có:
![]() \(1 + \log_{5}\left( x^{2} + 1 ight) \geq \log_{5}\left( mx^{2} + 4x + m ight)\)
\(1 + \log_{5}\left( x^{2} + 1 ight) \geq \log_{5}\left( mx^{2} + 4x + m ight)\)
![]() \(\Leftrightarrow \log_{5}\left\lbrack5\left( x^{2} + 1 ight) ightbrack \geq \log_{5}\left( mx^{2} + 4x +m ight)\)
\(\Leftrightarrow \log_{5}\left\lbrack5\left( x^{2} + 1 ight) ightbrack \geq \log_{5}\left( mx^{2} + 4x +m ight)\)
![]() \(\Leftrightarrow \left\{ \begin{matrix}
5\left( x^{2} + 1 ight) \geq mx^{2} + 4x + m \\
mx^{2} + 4x + m > 0 \\
\end{matrix} ight.\)
\(\Leftrightarrow \left\{ \begin{matrix}
5\left( x^{2} + 1 ight) \geq mx^{2} + 4x + m \\
mx^{2} + 4x + m > 0 \\
\end{matrix} ight.\)
![]() \(\Leftrightarrow \left\{ \begin{matrix}
(5 - m)x^{2} - 4x + 5 - m \geq 0\ \ \ (1) \\
mx^{2} + 4x + m > 0\ \ \ \ (2) \\
\end{matrix} ight.\)
\(\Leftrightarrow \left\{ \begin{matrix}
(5 - m)x^{2} - 4x + 5 - m \geq 0\ \ \ (1) \\
mx^{2} + 4x + m > 0\ \ \ \ (2) \\
\end{matrix} ight.\)
Bất phương trình đã cho có nghiệm đúng với mọi x khi cả (1) và (2) đúng với mọi x.
Với ![]() \(m = 0\) hoặc
\(m = 0\) hoặc ![]() \(m = 5\) không thỏa mãn đề bài.
\(m = 5\) không thỏa mãn đề bài.
Với ![]() \(m eq 0\) hoặc
\(m eq 0\) hoặc ![]() \(m eq 5\) để thỏa mãn đề bài thì:
\(m eq 5\) để thỏa mãn đề bài thì:
 \(\left\{ \begin{matrix}
5 - m > 0 \\
4 - (5 - m)^{2} \leq 0 \\
m > 0 \\
4 - m^{2} < 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}
m < 5 \\
\left\lbrack \begin{matrix}
m \leq 3 \\
m \geq 7 \\
\end{matrix} ight.\ \\
m > 0 \\
\left\lbrack \begin{matrix}
m > 2 \\
m < - 2 \\
\end{matrix} ight.\ \\
\end{matrix} ight.\)
\(\left\{ \begin{matrix}
5 - m > 0 \\
4 - (5 - m)^{2} \leq 0 \\
m > 0 \\
4 - m^{2} < 0 \\
\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}
m < 5 \\
\left\lbrack \begin{matrix}
m \leq 3 \\
m \geq 7 \\
\end{matrix} ight.\ \\
m > 0 \\
\left\lbrack \begin{matrix}
m > 2 \\
m < - 2 \\
\end{matrix} ight.\ \\
\end{matrix} ight.\)
![]() \(\Leftrightarrow 2 < m \leq
3\)
\(\Leftrightarrow 2 < m \leq
3\)






