Góc lượng giác Chân trời sáng tạo
a) Khái niệm góc lượng giác
Cho hai tia 
\(Oa,Ob\)
- Nếu một tia \(Om\) quay quanh gốc \(O\) của nó theo một chiều cố định bắt đầu từ vị trí tia \(Oa\) và dừng ở vị trí tia \(Ob\) thì ta nói tia \(Om\) quét một góc lượng giác có tia đầu \(Oa\), tia cuối \(Ob\), kí hiệu là \((Oa, Ob)\).
- Khi tia \(Om\) quay một góc \(α\), ta nói số đo của góc lượng giác \((Oa, Ob)\) bằng \(α\), kí hiệu là \(sđ(Oa, Ob) = α\).
Hình vẽ minh họa
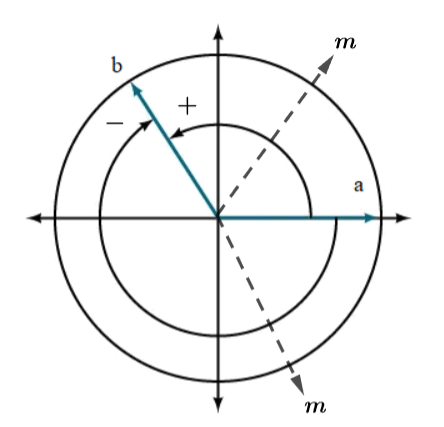
Chú ý: Với hai tia \(Oa,Ob\) cho trước, có vô số góc lượng giác tia đầu Oa và tia cuối Ob. Ta dùng chung kí hiệu \((Oa, Ob)\) cho tất cả các góc lượng giác này.
Ví dụ:
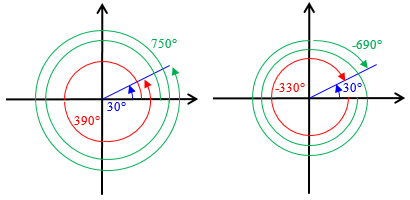
Nhận xét: Số đo của các góc lượng giác có cùng tia đầu \(Oa\) và tia cuối \(Ob\) sai khác nhau một bội nguyên của \(360^0\) nên có công thức tổng quát là:
\(sd\left( {Oa,Ob} \right) = {\alpha ^0} + k{.360^0};\left( {k \in \mathbb{Z}} \right)\)
Hay \(\left( {Oa,Ob} \right) = {\alpha ^0} + k{.360^0};\left( {k \in \mathbb{Z}} \right)\)
Với \({\alpha ^0}\) là số đo của một góc lượng giác bất kì có tia đầu \(Oa\) và tia cuối \(Ob\).
b) Hệ thức Chasles
Với ba tia \(Oa\), \(Ob\) và \(Oc\) bất kì ta có:
\(\left( {Oa,Ob} \right) + \left( {Ob,Oc} \right) = \left( {Oa,Oc} \right) + k{.360^0};\left( {k \in \mathbb{Z}} \right)\)
c) Đơn vị radian
Trên đường tròn bán kính \(R\) tùy ý, góc ở tâm chắn một chung có độ dài đúng bằng \(R\) được gọi là một góc có số đo 1 radian (hay 1rad).
Công thức chuyển đổi góc sang radian và ngược lại:
| \({\beta ^0} = \frac{{\pi .\beta }}{{{{180}^0}}}rad\) |
\(\alpha rad = {\left( {\frac{{180\alpha }}{\pi }} \right)^0}\) |
Ví dụ: a) Đổi từ độ sang radian các số đo sau: \({270^0}; - {480^0}\)
b) Đổi từ radian sang độ các số đo sau: \(5\pi ;\frac{{ - 12\pi }}{5}\)
Hướng dẫn giải
a) Ta có: \(\left\{ \begin{gathered}
{270^0} = 270.\frac{\pi }{{180}} = \frac{{3\pi }}{2} \hfill \\
- {480^0} = - 480.\frac{\pi }{{180}} = \frac{{ - 8\pi }}{3} \hfill \\
\end{gathered} \right.\)
b) Ta có: \(\left\{ \begin{gathered}
5\pi = 5\pi .{\left( {\frac{{180}}{\pi }} \right)^0} = {900^0} \hfill \\
\frac{{ - 12\pi }}{5} = \left( {\frac{{ - 12\pi }}{5}} \right).{\left( {\frac{{180}}{\pi }} \right)^0} = - {432^0} \hfill \\
\end{gathered} \right.\)
2. Đường tròn lượng giác
Trong mặt phẳng \(Oxy\), cho đường tròn tâm \(O\) bán kính bằng \(1\). Trên đường tròn này, chọn điểm \(A(1; 0)\) làm gốc:
- Chiều dương ngược chiều kim đồng hồ.
Hình vẽ minh họa
- Chiều âm cùng chiều kim đồng hồ.
Hình vẽ minh họa
Đường tròn cùng với gốc và chiều như trên được gọi là đường tròn lượng giác.
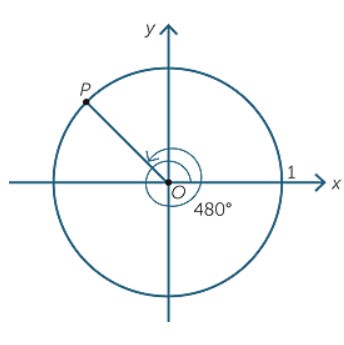
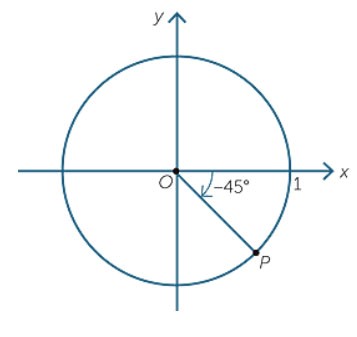
Ví dụ: Biểu diễn trên đường tròn lượng giác các góc \(-45^0\) và góc \(480^0\).
Hướng dẫn giải
a) Biểu diễn góc \(-45^0\)
b) Ta có: \({480^0} = {120^0} + {360^0}\)
Biểu diễn góc \(480^0\) như sau:
