Giá trị lượng giác của một góc lượng giác CTST
Định nghĩa: Giả sử điểm 
\(M\left( {x;y} \right)\) là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo \(\alpha\) (như hình vẽ):
- Hoành độ \(x = \cos \alpha\)
- Tung độ \(y = \sin \alpha\)
- \(\tan \alpha = \frac{y}{x} = \frac{{\sin \alpha }}{{\cos \alpha }};\left( {x \ne 0} \right)\) hay \(\tan \alpha\) xác định khi \(\alpha \ne \frac{\pi }{2} + k\pi ;\left( {k \in \mathbb{Z}} \right)\)
- \(\cot \alpha = \frac{x}{y} = \frac{{\cos \alpha }}{{\sin \alpha }};\left( {y \ne 0} \right)\) hay \(\cot \alpha\) xác định khi \(\alpha \ne k\pi ;\left( {k \in \mathbb{Z}} \right)\)
Chú ý:
+ Trục tung là trục sin, trục hoành là trục cosin.
+ Trục có gốc tại điểm \(A(1; 0)\) song song với trục sin là trục tang.
+ Trục có gốc tại điểm \(B(0; 1)\) song song với trục cosin là trục cotang.
a) Một số chú ý quan trọng
Với mọi góc lượng giác α và số nguyên k ta có:
| \(\sin \left( {\alpha + k2\pi } \right) = \sin \alpha\) |
\(\cos \left( {\alpha + k2\pi } \right) = \cos \alpha\) |
| \(\tan \left( {\alpha + k\pi } \right) = \tan \alpha\) |
\(\cot \left( {\alpha + k\pi } \right) = \cot \alpha\) |
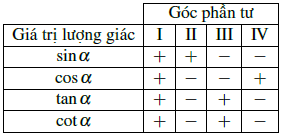
Chú ý: Dấu của các giá trị lượng giác của một góc lượng giác phụ thuộc vào vị trí điểm biểu diễn M trên đường tròn lượng giác.
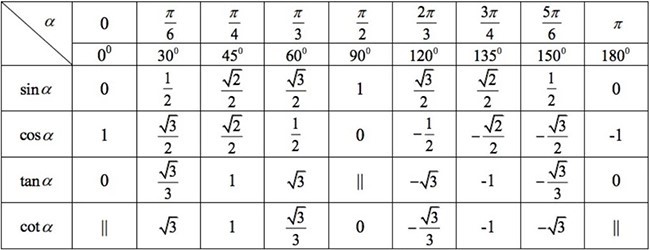
b) Giá trị lượng giác của các góc đặc biệt
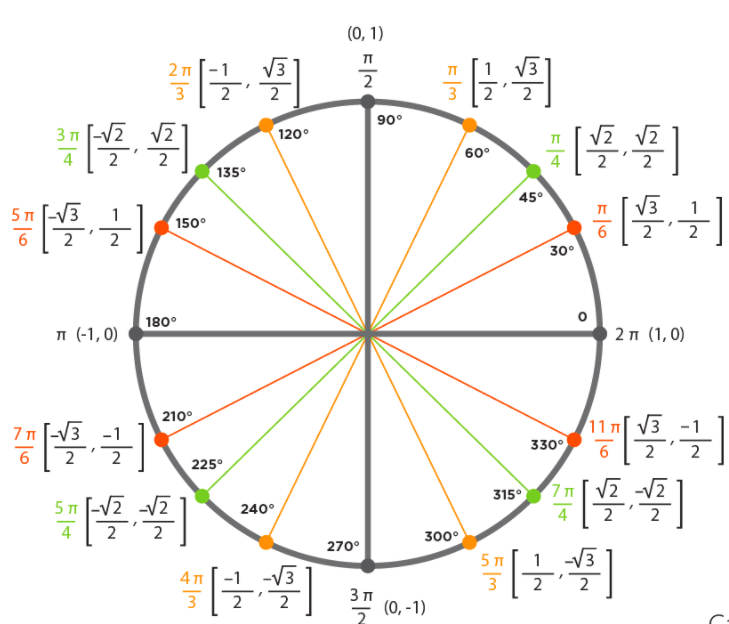
Biểu diễn trên vòng tròn lượng giác
Ví dụ: Cho góc \({0^0} < \alpha < {90^0}\). Xét dấu biểu thức: \(A = \sin \left( {\alpha + {{90}^0}} \right)\) và \(B = \cos \left( {{{270}^0} - \alpha } \right)\)?
Hướng dẫn giải
\(A = \sin \left( {\alpha + {{90}^0}} \right)\)
Ta có: \({0^0} < \alpha < {90^0} \Rightarrow {90^0} < \alpha + {90^0} < {180^0}\)
\(\Rightarrow A = \sin \left( {\alpha + {{90}^0}} \right) > 0\)
\(B = \cos \left( {{{270}^0} - \alpha } \right)\)
Ta có:
\({0^0} < \alpha < {90^0} \Rightarrow {180^0} < {270^0} - \alpha < {270^0}\)
\(\Rightarrow \cos \left( {{{270}^0} - \alpha } \right) < 0\)
2. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
| \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) |
\(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }};\left( {\alpha \ne \frac{\pi }{2} + k\pi ;k \in \mathbb{Z}} \right)\) |
| \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }};\left( {\alpha \ne k\pi ;k \in \mathbb{Z}} \right)\) |
\(\tan \alpha .\cot \alpha = 1;\left( {\alpha \ne \frac{{k\pi }}{2};k \in \mathbb{Z}} \right)\) |
Ví dụ: Rút gọn biểu thức: \(B = {\left( {\frac{{\sin x + \tan x}}{{\cos x + 1}}} \right)^2} + 1\)
Hướng dẫn giải
Ta có:
\(B = {\left( {\frac{{\sin x + \tan x}}{{\cos x + 1}}} \right)^2} + 1\)
\(B = {\left( {\dfrac{{\sin x + \dfrac{{\sin x}}{{\cos x}}}}{{\cos x + 1}}} \right)^2} + 1\)
\(B = {\left[ {\frac{{\sin x\left( {\cos x + 1} \right)}}{{\cos x\left( {\cos x + 1} \right)}}} \right]^2} + 1\)
\(B = {\left( {\frac{{\sin x}}{{\cos x}}} \right)^2} + 1 = {\tan ^2}x + 1 = \frac{1}{{{{\cos }^2}x}}\)
3. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
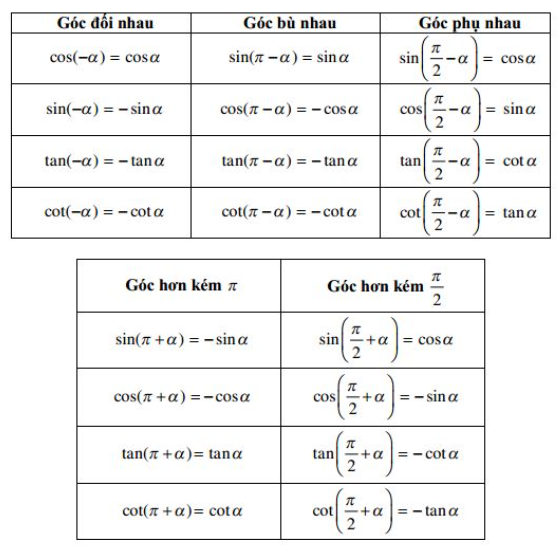
Ví dụ: Rút gọn biểu thức: \(A = \cos \left( {3\pi + x} \right) + \cos \left( {2\pi - x} \right) + \cos \left( {\frac{\pi }{2} + x} \right)\)
Hướng dẫn giải
Ta có:
\(A = \cos \left( {3\pi + x} \right) + \cos \left( {2\pi - x} \right) + \cos \left( {\frac{\pi }{2} + x} \right)\)
\(A = - \cos x + \cos \left( { - x} \right) - \sin x\)
\(A = - \cos x + \cos x - \sin x\)
\(A = - \sin x\)
