Giới hạn của dãy số CTST
a) Giới hạn 0 của dãy số
Ta nói dãy số 
\(\left( {{u_n}} \right)\) có giới hạn \(0\) khi \(n\) dần tới dương vô cực, nếu \(\left| {{u_n}} \right|\) nhỏ hơn một số dương bất kì cho trước, kể từ một số hạng nào đó trở đi, kí hiệu \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0\) hay \({u_n} \to 0\) khi \(n \to + \infty\). Ta còn viết là \(\lim {u_n} = 0\).
Chú ý:
- \(\lim \frac{1}{{{u^k}}} = 0,\left( {k \in {\mathbb{N}^*}} \right)\)
- \(\lim {q^n} = 0;\left( {q \in \mathbb{R},\left| q \right| < 1} \right)\)
Ví dụ: Chứng minh rằng các dãy số có giới hạn là 0.
|
a) |
b) |
Hướng dẫn giải
a) Ta có:
\(\left| {\frac{1}{{n\left( {2n + 3} \right)}}} \right| = \left| {\frac{1}{{2{n^2} + 3n}}} \right| \leqslant \frac{1}{{{n^2}}}\)
Mà \(\lim \frac{1}{{{n^2}}} = 0 \Rightarrow \lim \frac{1}{{n\left( {2n + 3} \right)}} = 0\)
b) \({u_n} = \frac{{{n^n}{{\left( {n + 2} \right)}^n}}}{{{{\left( {2n + 2} \right)}^{2n}}}} = \frac{{{{\left( {{n^2} + 2n} \right)}^n}}}{{{2^{2n}}{{\left( {n + 1} \right)}^{2n}}}}\)\(\leqslant \frac{{{{\left( {n + 1} \right)}^{2n}}}}{{{2^{2n}}{{\left( {n + 1} \right)}^{2n}}}} = {\left( {\frac{1}{2}} \right)^{2n}}\)
Mà \(\lim {\left( {\frac{1}{2}} \right)^{2n}} = 0 \Rightarrow \lim {u_n} = 0\)
b) Giới hạn hữu hạn của dãy số
Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn hữu hạn là số \(a\) khi n dần tới dương vô cực, nếu \(\lim \left( {{u_n} - a} \right) = 0\). Khi đó ta viết là \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\) hay \(\lim {u_n} = a\) hay \({u_n} \to a\) khi .
Chú ý: Nếu \({u_n} = c,\left( {c = const} \right)\) thì \(\lim {u_n} = \lim c = c\)
Ví dụ: Chứng minh rằng \(\lim \frac{{6n + 2}}{{n + 5}} = 6\)
Hướng dẫn giải
Ta có:
\(\lim \left( {\frac{{6n + 2}}{{n + 5}} - 6} \right) = \lim \left( {\frac{{ - 28}}{{n + 5}}} \right) = 0\)
(Do \(\left| {\frac{{28}}{{n + 5}}} \right| < \frac{{28}}{n}\))
Theo định nghĩa suy ra điều phải chứng minh.
2. Các phép toán về giới hạn hữu hạn của dãy số
Cho \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a;\mathop {\lim }\limits_{n \to + \infty } {v_n} = b\) và \(c\) là hằng số khi đó:
| \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b\) |
\(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} - {v_n}} \right) = a - b\) |
| \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n}.{v_n}} \right) = a.b\) |
\(\mathop {\lim }\limits_{n \to + \infty } \left( {\frac{{{u_n}}}{{{v_n}}}} \right) = \frac{a}{b};\left( {b \ne 0} \right)\) |
| \(\mathop {\lim }\limits_{n \to + \infty } \left( {c.{u_n}} \right) = c.a\) |
Nếu \(\left\{ \begin{gathered}
{u_n} \geqslant 0;\forall n \hfill \\
\mathop {\lim }\limits_{n \to + \infty } {u_n} = a \hfill \\
\end{gathered} \right.\) thì \(\left\{ \begin{gathered}
a > 0 \hfill \\
\mathop {\lim }\limits_{n \to + \infty } \sqrt {{u_n}} = \sqrt a \hfill \\
\end{gathered} \right.\). |
Ví dụ: Tính giới hạn:
|
a) |
b) |
|
c) |
d) |
Hướng dẫn giải
a) \(\lim \frac{{n\sqrt n - 1}}{{n + n\sqrt n }} = \lim \frac{{{n^{\frac{3}{2}}} - 1}}{{n + {n^{\frac{3}{2}}}}} = \lim \dfrac{{1 - \dfrac{1}{{{n^{\frac{3}{2}}}}}}}{{\frac{1}{{{n^{\frac{1}{2}}}}} + 1}} = 1\)
b) \(\lim \dfrac{{3{n^2} - 2n + 5}}{{2{n^2} + 5n - 3}} = \lim \dfrac{{3 - \dfrac{2}{n} + \dfrac{5}{{{n^2}}}}}{{2 + \dfrac{5}{n} - \dfrac{3}{{{n^2}}}}} = \dfrac{3}{2}\)
c) \(\lim \left( {\sqrt {{n^2} + 2n + 3} - n} \right)\)
\(= \lim \frac{{\left( {\sqrt {{n^2} + 2n + 3} + n} \right)\left( {\sqrt {{n^2} + 2n + 3} - n} \right)}}{{\sqrt {{n^2} + 2n + 3} + n}}\)
\(= \lim \left( {\frac{{2n + 3}}{{\sqrt {{n^2} + 2n + 3} + n}}} \right)\)
\(= \lim \left( {\dfrac{{2 + \dfrac{3}{n}}}{{\sqrt {1 + \dfrac{2}{n} + \dfrac{3}{{{n^2}}}} + 1}}} \right) = 1\)
d) \(\lim \dfrac{{{3^n} - {4^n} + {5^n}}}{{{3^n} + {4^n} - {5^n}}} = \lim \dfrac{{\dfrac{{{3^n}}}{{{5^n}}} - \dfrac{{{4^n}}}{{{5^n}}} + 1}}{{\dfrac{{{3^n}}}{{{5^n}}} + \dfrac{{{4^n}}}{{{5^n}}} - 1}} = - 1\)
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội \(q\) thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn.
Cấp số nhân lùi vô hạn có tổng là:
\(S = {u_1} + {u_2} + ... + {u_n} = \frac{{{u_1}}}{{1 - q}}\)
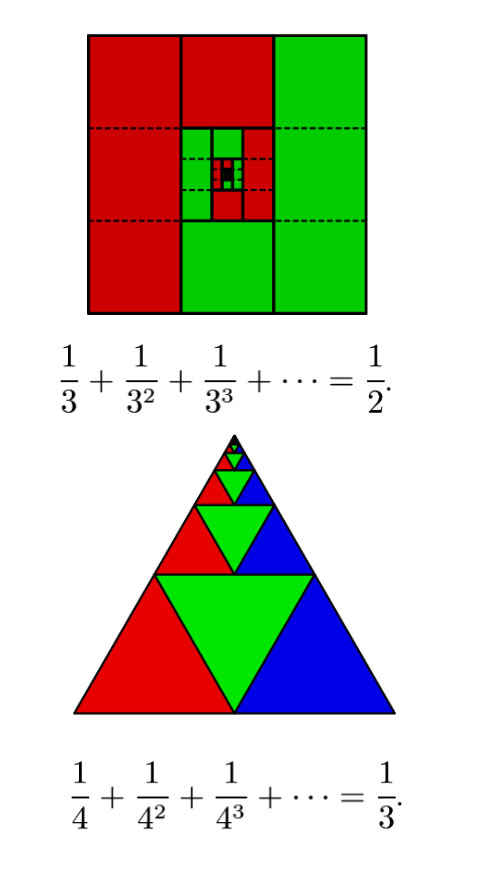
Ví dụ minh họa cấp số nhân lùi vô hạn:
Ví dụ: Tính tổng \(A = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{10}}}}\)
Hướng dẫn giải
Ta có:
\(A = \frac{1}{5} + \frac{1}{{{5^2}}} + \frac{1}{{{5^3}}} + ... + \frac{1}{{{5^{10}}}}\)
\(\Leftrightarrow A + 1 = {\left( {\frac{1}{5}} \right)^{10}} + {\left( {\frac{1}{5}} \right)^9} + ... + \frac{1}{{{5^3}}} + \frac{1}{{{5^2}}} + \frac{1}{5} + 1\)
\(\Leftrightarrow \left( {A + 1} \right)\left( {\frac{1}{5} - 1} \right) = [{\left( {\frac{1}{5}} \right)^{10}} + {\left( {\frac{1}{5}} \right)^9} +\)\(... + \frac{1}{{{5^3}}} + \frac{1}{{{5^2}}} + \frac{1}{5} + 1]\left( {\frac{1}{5} - 1} \right)\)
\(\Leftrightarrow \frac{4}{5}.\left( {A + 1} \right) = {\left( {\frac{1}{5}} \right)^{10}} - 1\)
\(\Leftrightarrow A + 1 = \frac{{{{5.5}^{10}} - 1}}{{{{4.5}^{10}}}}\)
\(\Leftrightarrow A = \frac{{{{5.5}^{10}} - 1}}{{{{4.5}^{10}}}} - 1 \Leftrightarrow A = \frac{{{5^{10}} - 1}}{{{{4.5}^{10}}}} - 1\)
\(\Leftrightarrow A = \frac{1}{4}\left[ {1 - {{\left( {\frac{1}{5}} \right)}^{10}}} \right]\)
4. Giới hạn vô cực
- Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là \(+ \infty\) nếu \(n \to + \infty\) lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi, kí hiệu \(\lim {u_n} = + \infty\) hay \({u_n} \to + \infty\) khi \(n \to + \infty\).
- Ta nói dãy số \(\left( {{u_n}} \right)\) có giới hạn là \(- \infty\) khi \(n \to + \infty\) nếu \(\lim \left( { - {u_n}} \right) = + \infty\) kí hiệu là \(\lim {u_n} = - \infty\) hay \({u_n} \to - \infty\) khi \(n \to + \infty\).
Chú ý:
a) \(\lim {u_n} = + \infty\) khi và chỉ khi \(\lim \left( { - {u_n}} \right) = - \infty\)
b) Nếu \(\lim {u_n} = + \infty\) hoặc \(\lim {u_n} = - \infty\) thì \(\lim \frac{1}{{{u_n}}} = 0\)
c) Nếu \(\lim {u_n} = 0\) và \({u_n} > 0\) với mọi n thì \(\lim \frac{1}{{{u_n}}} = + \infty\)
Ví dụ: Tính giới hạn:
|
a) |
b) |
Hướng dẫn giải
a) \(\lim \left( {\sqrt[3]{{1 + 2n - {n^3}}} - n} \right)\)
\(= \lim \left[ {\sqrt[3]{{{n^3}\left( {\frac{1}{{{n^3}}} + \frac{2}{{{n^2}}} - 1} \right)}} - n} \right]\)
\(= \lim \left( { - 2n} \right) = - \infty\)
b) \(\lim \left( {n + \sqrt {{n^2} - n + 1} } \right)\)
\(= \lim \left( {n + n\sqrt {1 - \frac{1}{n} + \frac{1}{{{n^2}}}} } \right) = \lim \left( {2n} \right) = + \infty\)
