Hai đường thẳng vuông góc CTST
Góc giữa hai đường thẳng 
\(a, b\) trong không gian, kí hiệu \((a; b)\) là góc giữa hai đường thẳng \(a’, b’\) cùng đi qua một điểm và lần lượt song song hoặc trùng với \(a\) và \(b\).
Hình vẽ minh họa
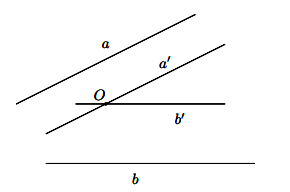
Chú ý:
- Để xác định góc giữa hai đường thẳng \(a, b\) ta có thể lấy một điểm \(O\) nằm trên một trong hai đường thẳng đó và vẽ đường thẳng song song với đường thẳng còn lại.
- Góc giữa hai đường thẳng nhận giá trị từ \(0^0\) đến \(180^0\).
Ví dụ: Cho tứ diện \(ABCD\). Gọi trung điểm của các cạnh \(AB\) và \(CD\) lần lượt là \(M\) và \(N\). Biết rằng \(MN = a\sqrt {3a} ;AD = BC = 2a\). Xác định và tính góc giữa hai đường thẳng \(AD\) và \(BC\)?
Hướng dẫn giải
Hình vẽ minh họa
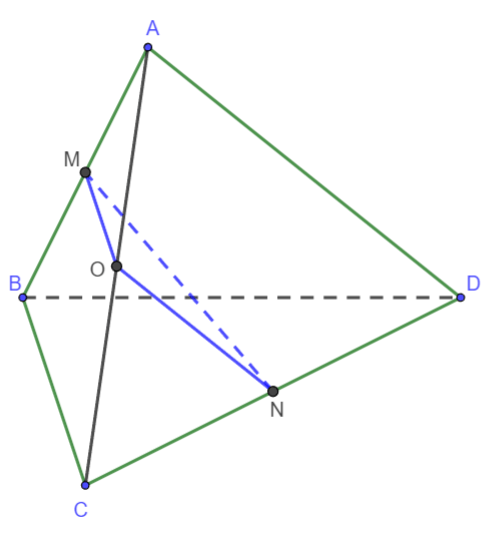
Gọi O là trung điểm AC.
Vì \(OM, ON\) lần lượt là đường trung bình của hai tam giác \(ABC\) và \(CAD\) nên \(\left\{ \begin{gathered}
OM//BC,OM = \frac{1}{2}CB = a \hfill \\
ON//AD,ON = \frac{1}{2}AD = a \hfill \\
\end{gathered} \right.\)
Xét tam giác OMN có:
\(\cos \widehat {MON} = \frac{{O{M^2} + O{N^2} - M{N^2}}}{{2OM.ON}}\)
\(= \frac{{{a^2} + {a^2} - {{\left( {a\sqrt 3 } \right)}^2}}}{{2.a.a}} = \frac{1}{2}\)
\(\Rightarrow \widehat {MON} = {120^0}\)
\(\Rightarrow \left( {AD,BC} \right) = \left( {ON,OM} \right)\)\(= {180^0} - {120^0} = {60^0}\)
2. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng a, b được gọi là vuông góc với nhau, kí hiệu là nếu góc giữa chúng bằng \(90^0\).
Ví dụ: Cho tứ diện \(ABCD\). Gọi trung điểm cạnh \(AC\) và \(BD\) lần lượt là \(M\) và \(N\). Chứng minh đường thẳng \(AB\) vuông góc với đường thẳng \(CD\). Biết \(AB = 2\sqrt 2 a;CD = 2a;MN = a\sqrt 3\).
Hướng dẫn giải
Hình vẽ minh họa
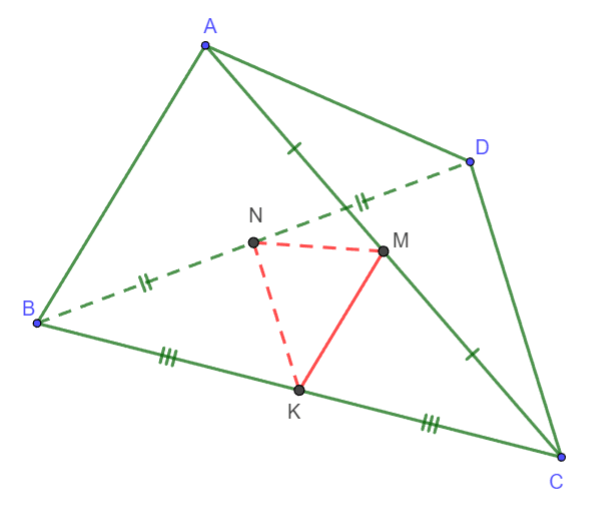
Gọi K là trung điểm cạnh \(BC\)
Ta có: \(NK,MK\) lần lượt là đường trung bình của tam giác BCD và tam giác ABC nên \(NK = a;MK = a\sqrt 2\)
Do đó \(M{N^2} = 3{a^2} - M{K^2} + N{K^2}\)
Suy ra tam giác MNK vuông tại K \(\Rightarrow MK \bot NK\)
Mà \(\left\{ \begin{gathered}
MK//AB \hfill \\
NK//CD \hfill \\
\end{gathered} \right.\) nên \(\left( {AB,CD} \right) = \left( {MK,NK} \right) = {90^0}\)
\(\Rightarrow AB \bot CD\)
