Biến cố hợp và quy tắc cộng xác suất CTST
Cho hai biến cố 
\(A\) và \(B\). Biến cố “\(A\) hoặc \(B\) xảy ra”, kí hiệu là \(A \cup B\), được gọi là biến cố hợp của \(A\) và B.
Hình vẽ minh họa
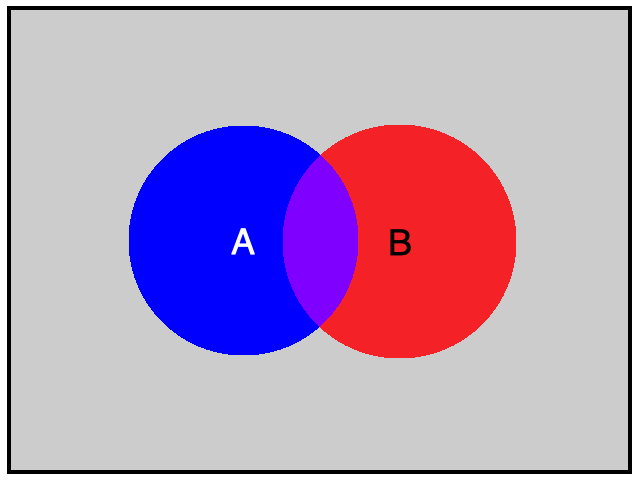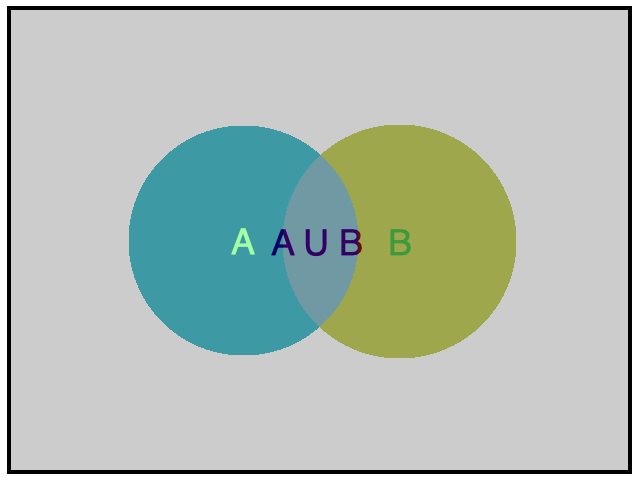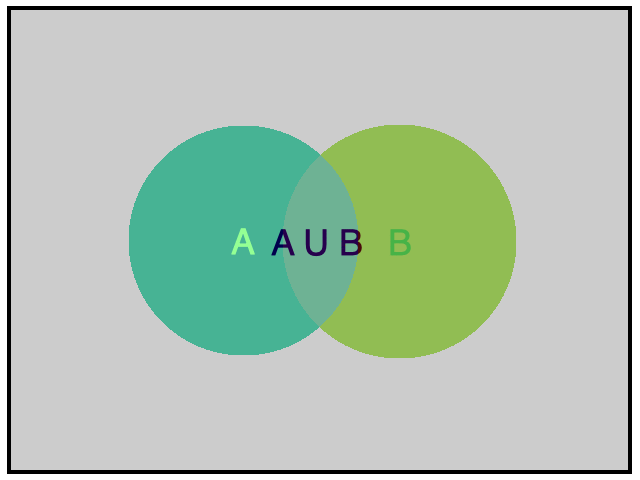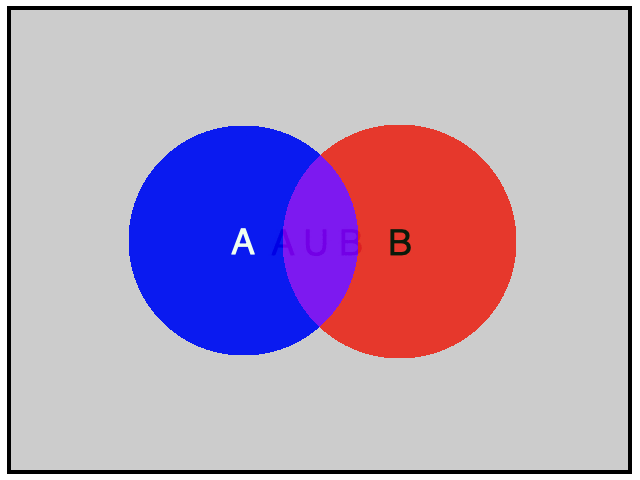
Chú ý: Biến cố \(A \cup B\) xảy ra khi có ít nhất một trong hai biến cố \(A\) hoặc \(B\) xảy ra. Tập hợp mô tả biến cố \(A \cup B\) là hợp của hai tập hợp mô tả biến cố \(A\) và biến cố \(B\).
2. Quy tắc cộng xác suất
a) Quy tắc cộng cho hai biến cố xung khắc
Cho hai biến cố xung khắc \(A\) và \(B\). Khi đó:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
Ví dụ: Một hộp đựng 9 tấm thẻ được đánh số từ 1 tới 9, hai tấm thẻ khác nhau đánh hai số khác nhau. Rút ngẫu nhiên đồng thời hai tấm thẻ từ hộp. Xét các biến cố sau: A: "Cả hai tấm thẻ đều đánh số chẵn", B: "Chỉ có một tấm thẻ đánh số chẵn", C: "Tích hai số đánh trên hai tấm thẻ là một số chẵn". Tính xác suất để biến cố C xảy ra.
Hướng dẫn giải
Ta có: A và B là hai biến cố xung khắc nên \(P\left( C \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\)
\(P\left( A \right) = \frac{{C_4^2}}{{C_9^2}} = \frac{1}{6}\)
\(P\left( B \right) = \frac{{C_4^1.C_5^1}}{{C_9^2}} = \frac{5}{9}\)
\(\Rightarrow P\left( C \right) = P\left( A \right) + P\left( B \right) = \frac{1}{6} + \frac{5}{9} = \frac{{13}}{{18}}\)
b) Quy tắc cộng cho hai biến cố bất kì
Cho hai biến cố \(A\) và \(B\) bất kì. Khi đó:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\)
Ví dụ: Một khu phố có 50 hộ gia đình trong đó có 18 hộ nuôi chó, 16 hộ nuôi mèo và 7 hộ nuôi cả chó và mèo. Chọn ngẫu nhiên một hộ trong khu phố trên, tính xác suất để: Hộ đó nuôi chó hoặc nuôi mèo.
Hướng dẫn giải
Gọi các biến cố A: "Chọn được hộ nuôi chó" và B: "Chọn được hộ nuôi mèo".
Ta có:
\(n\left( \Omega \right) = 50\)
\(P\left( A \right) = \frac{{18}}{{50}} = \frac{9}{{25}}\)
\(P\left( B \right) = \frac{{16}}{{50}} = \frac{8}{{25}}\)
\(P\left( {AB} \right) = \frac{7}{{50}}\)
Xác suất để chọn được hộ nuôi chó hoặc nuôi mèo là:
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right)\)
\(= \frac{9}{{25}} + \frac{8}{{25}} - \frac{7}{{50}} = \frac{{27}}{{50}} \approx 0,54\)
