Đề thi học kì 1 Toán 9 Kết nối tri thức CV 7991 Đề 4

Đề kiểm tra cuối kì 1 toán 9 theo công văn 7991

Đề thi học kì 1 Toán 9 Kết nối tri thức theo công văn 7991 được biên soạn bám sát nội dung chương trình mới của Bộ Giáo dục và Đào tạo, đảm bảo đúng chuẩn năng lực – phẩm chất học sinh theo định hướng phát triển năng lực. Bộ đề giúp học sinh ôn luyện toàn diện các mảng kiến thức trọng tâm như: Căn bậc hai, Hệ thức lượng trong tam giác vuông, phương trình, hệ phương trình, bất đẳng thức, ... cùng các bài toán thực tế vận dụng.

Với cấu trúc và mức độ câu hỏi tương tự đề kiểm tra chính thức, đây là tài liệu hữu ích giúp giáo viên tham khảo, học sinh tự đánh giá năng lực và chuẩn bị hiệu quả cho kỳ thi học kì 1 môn Toán lớp 9.

Giới thiệu tài liệu đề thi Toán 9 sách Kết nối tri thức

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 2 môn Toán lớp 9.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

A. TRẮC NGHIỆM (7 ĐIỂM)

Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. \(2xy + y = 3\).       B. \(y - 2x = 0\).         C. \(2x + 2y = 1\).            D. \(0x + 0y = 0\).

Câu 2: Phương trình bậc nhất hai ẩn \(x - 2y = 4\) có một nghiệm là:

A. (1; -1).         B. (-2;1).          C. (2; 1).           D. (2; -1).

Câu 3: Hệ phương trình \(\left\{ \begin{matrix} - x + 2y = 3 \\ x - y = 1 \end{matrix} \right.\) có nghiệm là:

A. (-4; 5).                B. (5; -4).            C. (5; 4).              D. (1; 0).

Câu 4: Cho bất đẳng thức \(a < b\). Khẳng định nào sau đây là đúng.

A. \(a + 3 > b + 3\).        B. \(a + 3 < b + 3\) .          C.  \(a.2 > b.2\).       D.\(- 3a < - 3 b\).

Câu 5: Bất phương trình nào là bất phương trình bậc nhất một ẩn

A. \(0x - 3 > 0\).          B. \(2x + 5y > 0\).       C. \(2xy > 0\) .        D. \(3x + 2y < x - 4\).

Câu 6. Tất cả các giá trị thực của x thoả mãn \(\sqrt[3]{2x + 1} > - 3\) là:

A. \(x = - 14.\)             B. \(x < - 14.\)              C. \(x > - 14.\)       D. \(x > - 12.\)

Câu 7. Tập hợp \(S = \left\{ 2 \right\}\) là nghiệm của phương trình nào?

A. \(x + 2 = 0\).       B. \(2x + 4 = 0\).             C. \(- 5x + 10= 0\).                D. \(3x + 6 = 0\).

Câu 8. Cho ∆ABC vuông tại A có \(BA = 5;AC = 13\). Giá trị \(\cos C\) bằng:

A. \(\frac{12}{13}\).              B. \(\frac{5}{13}\).            C. \(\frac{5}{12}\).           D. \(\frac{12}{5}\).

Câu 9. Trong các khẳng định sau, khẳng định nào sai?

A. \(\cos35^{0} = \sin55^{0}\).          B. \(\sin65^{0} = \cos25^{0}\).   

C. \(\tan25^{0} = \cot65^{0}\).          D. \(\cos25^{0} =\cos65^{0}\)

Câu 10. Hình vành khuyên giới hạn bởi hai đường tròn \(\left( O;\mathbf{\ }2\mathbf{\ }cm \right)\) và \(\left( O;\mathbf{\ }R\mathbf{\ }cm \right)\); \((R > 2)\) có diện tích là \(32\pi\mathbf{\ }cm^{2}\), khi đó \(R\) bằng:

A. \(6\mathbf{\ }cm\).        B. \(\mathbf{5\ }cm\).         C. \(\mathbf{4\ }cm\).            D. \(\mathbf{3\ }cm\).

Câu 11: Khẳng định nào sau đây là đúng?

A. Đường tròn là hình có 1 tâm đối xứng, không có trục đối xứng.

B. Đường tròn là hình có 1 tâm đối xứng, có 1 trục đối xứng.

C. Đường tròn là hình có 1 tâm đối xứng, có vô số trục đối xứng.

D. Đường tròn là hình không có tâm đối xứng, có vô số trục đối xứng.

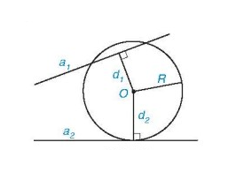
Câu 12: Cho đường tròn \((O;R)\) và hai đường thẳng \(a_{1}\) và \(a_{2}\). Gọi \(d_{1},d_{2}\) lần lượt là khoảng cách từ điểm \(O\) đến \(a_{1}\) và \(a_{2}\). Biết rằng \((O)\) cắt \(a_{1}\) và tiếp xúc với \(a_{2}\) (hình vẽ). Khi đó:

A.\(d_{1} = R;d_{2} < R.\)                     B.\(d_{1} < R;d_{2} = R.\)

C. \(d_{1} > R;d_{2} = R.\)                    D. \(d_{1} < R;d_{2} < R.\)

Phần 2. Câu trắc nghiệm đúng sai (2 điểm)

Thí sinh trả lời câu 13 và câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 13 (1 điểm): Cho tam giác ABC vuông tại A, có \(AB = 3cm\), \(BC = 5cm\). Xét tính đúng sai của các khẳng định dưới đây:

Câu 14 (1 điểm): Để mở rộng kinh doanh, một cửa hàng đã vay \(600\) triệu đồng kì hạn \(12\)tháng từ hai ngân hàng A và B với lãi suất lần lượt là \(8\)% năm và \(9\)% năm. Tổng số tiền lãi một năm phải trả cho cả hai ngân hàng đó là \(51,5\) triệu đồng. Gọi \(x\) và \(y\) (triệu đồng) lần lượt là số tiền mà cửa hàng đã vay từ mỗi ngân hàng A và B \((x > 0;\ y > 0)\). Xét tính đúng sai của các mệnh đề sau:

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2 điểm)

Trong mỗi câu hỏi từ 15 đến 18, hãy viết câu trả lời đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Thực hiện các phép tính sau:

a. \(\sqrt{21,8^{2} - 18,2^{2}}\)                    b. \(2\left( \sqrt[3]{27} + 5\sqrt[3]{216} \right).\sqrt[3]{\frac{1}{64}}.\)

Câu 16. Bạn A quan sát đứng cách một cái cây \(25m\), nhìn thẳng đỉnh cây dưới một góc nâng \(42^{0}\) so với phương ngang của mặt đất (như hình vẽ).

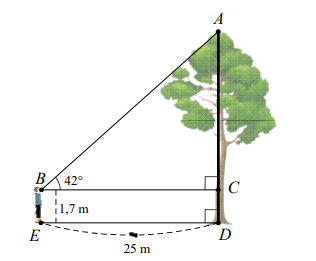
Biết khoảng cách từ mắt bạn A đến mặt đất bằng \(1,7m\). Hãy tính chiều cao của cây (làm tròn kết quả đến chữ số thập phân thứ nhất của mét).

Câu 17. Cho đường thẳng d có phương trình \((2m - 4)x + (m - 1)y = m - 5\). Tìm các giá trị của m tham số d để đi qua gốc tọa độ?

Câu 18. Để hưởng ứng phong trào “Trồng cây gây rừng”, lớp 9A có kế hoạch trồng ít nhất 100 cây xanh. Lớp 9A đã trồng được 54 cây. Để đạt được kế hoạch đề ra, lớp 9A cần trồng thêm ít nhất bao nhiêu cây xanh nữa?

B. TỰ LUẬN (3 ĐIỂM)

Bài 1 (1 điểm). Thực hiện theo các yêu cầu dưới đây:

a) Cho biểu thức: \(A = \left( \frac{\sqrt{x}}{\sqrt{x} - 2} + \frac{\sqrt{x}}{\sqrt{x} + 2} \right).\frac{x - 4}{2\sqrt{x}\left( \sqrt{x} + 1 \right)};(x > 0;x \neq 4)\). Rút gọn biểu thức A.

b) Để hoàn thành một công việc, hai tổ làm chung và dự kiến hoàn thành sau 4 giờ. Trên thực tế sau 3 giờ hai tổ làm chung thì tổ I bị điều đi làm việc khác, tổ II hoàn thành nốt công việc còn lại trong 3 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ hoàn thành công việc?

Bài 2 (1,5 điểm). Từ điểm \(A\) nằm ngoài đường tròn tâm \(O\), bán kính \(R\), vẽ hai tiếp tuyến \(AB\) và \(AC\) (B và C là hai tiếp điểm).

a) Chứng minh rằng: \(AB = AC\) và \(OA\) vuông góc với \(BC\) tại \(H\).

b) Vẽ đường kính \(BD\), đoạn \(AD\) cắt đường tròn tại \(E\). Chứng minh \(BE\) vuông góc với \(AD\) tại \(E\) và \(AC^{2} = AE.AD\).

c) Chứng minh: \(\widehat{AHE} = \widehat{EDB}\).

Bài 3 (0,5 điểm). Cho các số dương \(a,\ b,\ c\) thỏa mãn \(a + b + c = 2023\). Tìm giá trị lớn nhất của biểu thức: \(Q = \sqrt{ab + 2023c} + \sqrt{bc + 2023a} + \sqrt{ac + 2023b}\ \ .\)

------------ Hết -----------

 Bạn muốn xem toàn bộ tài liệu? Hãy nhấn Tải về ngay!