Đề thi học kì 1 Toán 9 Chân trời sáng tạo (Theo công văn 7991) Đề 4

Đề kiểm tra cuối kì 1 toán 9 CTST (CV 7991)

Đề thi cuối học kì 1 lớp 9 môn Toán sách Chân trời sáng tạo được VnDoc biên soạn bám sát nội dung cấu trúc ma trận đề thi theo Công văn 7991 của Bộ Giáo dục và Đào tạo. 

Giới thiệu tài liệu đề thi Toán 9 sách Chân trời sáng tạo

Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 1 môn Toán lớp 9.

Họ và tên học sinh: …………………………….. Lớp: …………………………..

A. TRẮC NGHIỆM (7 ĐIỂM)

Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.

Câu 1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. \(2x - 5y = 1\)        B.\(0x + 0y = - 2\)        C. \(2z + 3y = z\)      D.\(x - 0y = z^{2}\)

Câu 2. Phương trình bậc nhất hai ẩn \(\frac{12}{3}x + y = 3\) có hệ số \(a;b\) lần lượt là

A.\(a = 1;b = \frac{12}{3}\) B. \(a = \frac{12}{3};b = 3\) C. \(a = \frac{12}{3};b = 1\) D. \(a = 3;b = 1\)

Câu 3. Cho hệ phương trình sau: \(\left\{ \begin{matrix} 2x + 3y = 7 \\ 2x + 2y = 4 \end{matrix} \right.\) Chọn khẳng định đúng.

A. Lấy (1) – (2) ta được phương trình một ẩn là: \(x = 3\)

B. Lấy (1) – (2) ta được phương trình một ẩn là: \(y = 3\)

C. Lấy (1) – (2) ta được phương trình một ẩn: \(x = 11\)

D. Lấy (1) – (2) ta được phương trình một ẩn là: \(y = 11\)

Câu 4. Cặp số \((2; - 1)\)là nghiệm của hệ phương trình nào?

A. \(\left\{ \begin{matrix} 3x - y = - 1 \\ x - 3y = 5 \end{matrix} \right.\)      B. \(\left\{ \begin{matrix} y = 1 \\ x - 3y = 4 \end{matrix} \right.\)      C. \(\left\{ \begin{matrix} 3x - y = 1 \\ x - 3y = 4 \end{matrix} \right.\)      D. \(\left\{ \begin{matrix} y = - 1 \\ x - 3y = 5 \end{matrix} \right.\)

Câu 5. Bất phương trình nào sau đây không phải là bất phương trình bậc nhất một ẩn?

A. \(- x + 5 > 0.\)           B. \(\sqrt{2}y - 3x + 5 > 0.\)      C. \(- x - 1 > 0.\)            D. \(x + 9 \leq 0.\) 

Câu 6.  \(x = 1;x = 5\) là hai nghiệm của phương trình nào dưới đây?

A. \((5 - x)(x + 1) = 0.\)             B.  \((5 - x)(x - 1) = 0.\)

C.  \((5 + x)(x + 1) = 0.\)               D.  \((5 + x)( - x - 1) = 0.\)

Câu 7. Điều kiện xác định của phương trình: \(1 - \frac{3}{1 - x} = 0\) là:

A. \(x \neq 3.\)        B. \(x \neq 1.\)        C. \(x \neq - 1.\)           D. \(x \neq - 3.\)

Câu 8. Nghiệm của bất phương trình \(- x + 1 > 0\) là:

A.  \(x > 1.\)         B.\(x < 1.\)        C.  \(x \geq 1.\)      D.\(x \leq 1.\)

Câu 9. Biểu thức \(\sqrt{2x}\) có nghĩa khi:

A. \(x > 2.\)             B. \(x \geq 0.\)                C. \(x \leq 0.\)         D. Với mọi x\(\in\)R\(.\)

Câu 10. Tính giá trị biểu thức \(B = \sqrt[3]{( - 15)^{3}} + \sqrt[3]{(19)^{3}}\) ta được kết quả:

A. \(4\)             B.\(34\)        C. \(- 4\)             D. \(- 34\)

Câu 11. Cho đường tròn\((O;\ 10cm)\). Khi đó dây lớn nhất của đường tròn có độ dài là:

A.\(\ 5\ cm\)        B.\(\ 10\ cm\)      C. \(15\ cm\)       D. \(20\ cm\)

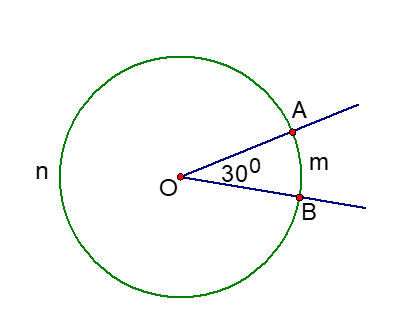
Câu 12. Cho hình vẽ bên. Số đo \(\widehat{AnB}\)= …

A.\(\ 60^{\circ}\).        B. \(330^{\circ}\).     C.\(\ 120^{\circ}\).     D. \(90^{\circ}\).

Phần 2. Câu trắc nghiệm đúng sai (2 điểm)

Thí sinh trả lời câu 13 và câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.

Câu 13 (1 điểm): Cho hai đường tròn \((O;4\ cm)\) và \((O';3\ cm)\).

a) Nếu \(OO' = 7cm\) thì hai đường tròn trên tiếp xúc ngoài

b) Nếu \(OO' > 7cm\) thì hai đường tròn trên cắt nhau.

c) Nếu hai đường tròn trên cắt nhau thì số giá trị nguyên mà độ dài \(OO'\) có thể nhận được (đơn vị cm) là \(4\).

d) Nếu \(OO' = 5\ cm\), hai đường tròn trên cắt nhau tại \(A\) và \(B\) thì độ dài \(AB\) là \(4,8\ cm\)

Câu 14 (1 điểm): Một quá táo có giá 22 nghìn đồng, một quả lê có giá 10 nghìn đồng. Bạn An có 300 nghìn đồng, bạn ấy muốn mua mỗi loại ít nhất 6 quả và tổng số hai loại quả mua được là nhiều nhất. Gọi \(x\) (quả) là tổng số quả táo và quả lê bạn An có thể mua được \((x \in N,\ x \geq 12)\).

a) Do mỗi loại bạn An mua ít nhất 6 quả và giá của mỗi quả táo cao hơn mỗi quả lê, nên bạn An chỉ nên mua 6 quá táo để số quả lê mua được là nhiều nhất.

b) Số tiền bạn An dùng để mua lê là \(10\ (x - 6)\ (\)nghìn đồng).

c) Bất phương trình biểu diễn số tiền bạn An dùng để mua hai loại quả là:\(132 + 10\ (x - 6)\ \leq 300\).

d) Bạn An có thể mua được nhiều nhất 20 quá táo và lê.

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2 điểm)

Trong mỗi câu hỏi từ 15 đến 18, hãy viết câu trả lời đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Câu 15. Tính giá trị của biểu thức: \(5\sqrt{48} - 2\sqrt{108} + \frac{\sqrt{42}}{\sqrt{14}} - 2\sqrt{147}\)?

Câu 16. Tính diện tích hình quạt tròn có bán kính \(4\ cm\), ứng với cung \(36^{0}\).

Câu 17. Trên một khúc sông với hai bờ song song với nhau, có một chiếc đò dự định chèo qua sông từ vị trí \(A\) ở bờ bên này sang vị trí \(B\) ở bờ bên kia, đường thẳng \(AB\) vuông góc với các bờ sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị tri \(C\) cách \(B\) một khoảng bằng \(30\ \ m\). Biết khúc sông rộng \(150\ \ m\). Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây).

Câu 18. Cho ΔABC vuông tại A có AB = 6 cm; AC = 8cm. Hỏi bán kính đường tròn đi qua ba điểm A; B; C bằng bao nhiêu centimet?

B. TỰ LUẬN (3 ĐIỂM)

Bài 1 (1, 5 điểm). a. Với \(x > 0\) và \(x \neq 1\) rút gọn biểu thức:

\(Q = \frac{\sqrt{x}}{\sqrt{x} - 1} - \frac{2}{\sqrt{x} + 1} - \frac{2}{x - 1}\).

b. Tìm số tự nhiên có hai chữ số biết tổng của hai chữ số đó bằng 10. Nếu thêm chữ số 0 vào giữa hai chữ số thì được số tự nhiên có ba chữ số, lấy số tự nhiên có ba chữ số này chia cho số cần tìm thì được thương là 7 và dư là 12.

Bài 2 (1 điểm). Cho đường tròn (O; R), đường kính AB. Lấy điểm C thuộc (O; R) sao cho AC > BC. Kẻ đường cao CH của \(\Delta\)ABC (H\(\ \in\) AB), kéo dài CH cắt (O; R) tại điểm D (D ≠ C). Tiếp tuyến tại điểm A và tiếp tuyến tại điểm C của đường tròn (O; R) cắt nhau tại điểm M. Gọi I là giao điểm của OM và AC. Hai đường thẳng MC và AB cắt nhau tại F.

a) Chứng minh DF là tiếp tuyến của (O; R).

b) Chứng minh: AF.BH = BF.AH.

Bài 3 (0,5 điểm). Cho x, y, z là các số thực dương thỏa mãn \(xy + yz + zx = 5\)

Tìm giá trị nhỏ nhất của biểu thức: \(P = \frac{3x + 3y + 2z}{\sqrt{6(x^{2} + 5)} + \sqrt{6(y^{2} + 5)} + \sqrt{z^{2} + 5}}\)

- Hết -

Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.