Đề thi học kì 1 Toán 9 Chân trời sáng tạo (Theo công văn 7991) Đề 2
Đề kiểm tra cuối kì 1 toán 9 CTST (Theo CV 7991)
Đề thi cuối học kì 1 lớp 9 môn Toán sách Chân trời sáng tạo được VnDoc biên soạn bám sát nội dung cấu trúc ma trận đề thi theo Công văn 7991 của Bộ Giáo dục và Đào tạo.
Giới thiệu tài liệu đề thi Toán 9 sách Chân trời sáng tạo
Cấu trúc đề thi: Kết hợp giữa trắc nghiệm và tự luận (tỉ lệ 70% trắc nghiệm, 30% tự luận).
Mức độ: Nhận biết - Thông hiểu - Vận dụng: 40% - 30% - 30%
Phần 1: Trắc nghiệm khách quan (TNKQ) gồm:
- TNKQ Nhiều lựa chọn: Gồm 12 câu hỏi ở dạng thức trắc nghiệm nhiều lựa chọn, cho 4 phương án chọn 1 đáp án đúng. Mỗi câu trả lời đúng thí sinh được 0,25 điểm.
- TNKQ Đúng - Sai: Gồm 2 câu hỏi ở dạng thức trắc nghiệm dạng Đúng/Sai. Mỗi câu hỏi có 4 ý, tại mỗi ý thí sinh lựa chọn Đúng hoặc Sai. Mỗi ý đúng thí sinh được 0,25 điểm
- TNKQ trả lời ngắn: Gồm 4 câu hỏi ở dạng thức trắc nghiệm trả lời ngắn. Học sinh ghi lại kết quả theo yêu cầu của đề bài, tại mỗi ý đúng thí sinh được 0,5 điểm.
Phần 2. Tự luận (gồm 3 câu hỏi), thí sinh trình bày câu trả lời ra giấy.
Hy vọng thông qua nội dung tài liệu, sẽ giúp bạn học ôn tập, củng cố kiến thức, chuẩn bị tốt cho bài kiểm tra đánh giá học kì 1 môn Toán lớp 9.
|
Trường THCS Đề thi theo CV 7991 - Số 2 Chân trời sáng tạo |
MÔN: TOÁN - LỚP 9 NĂM HỌC: 2025 – 2026 Thời gian làm bài: 90 phút |
Họ và tên học sinh: …………………………….. Lớp: …………………………..
A. TRẮC NGHIỆM (7 ĐIỂM)
Phần I. Câu trắc nghiệm nhiều phương án lựa chọn (3 điểm)
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn 1 phương án.
Câu 1. Căn bậc hai của số thực không âm a là số X thoả mãn:
A. ![]() \(a^{2} = x\) B.
\(a^{2} = x\) B. ![]() \(x^{2} = a\). C.
\(x^{2} = a\). C. ![]() \(x \geq 0\) và
\(x \geq 0\) và ![]() \(x^{2} = a\). D.
\(x^{2} = a\). D. ![]() \(x \geq 0\) và
\(x \geq 0\) và ![]() \(\sqrt{x} = a\).
\(\sqrt{x} = a\).
Câu 2. Cho tam giác ![]() \(ABC\) vuông tại
\(ABC\) vuông tại ![]() \(A\). Ta có sin
\(A\). Ta có sin ![]() \(B\) bằng:
\(B\) bằng:
A. ![]() \(\frac{AB}{AC}\). B.
\(\frac{AB}{AC}\). B. ![]() \(\frac{AC}{AB}\). C.
\(\frac{AC}{AB}\). C. ![]() \(\frac{AB}{BC}\). D.
\(\frac{AB}{BC}\). D. ![]() \(\frac{AC}{BC}\).
\(\frac{AC}{BC}\).
Câu 3. Góc nào sau đây trong hình vẽ là góc nội tiếp đường tròn tâm ![]() \(O\) ?
\(O\) ?
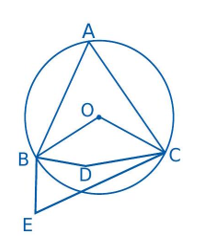
A. ![]() \(\widehat{BAC}\). B.
\(\widehat{BAC}\). B. ![]() \(\widehat{BOC}\). C.
\(\widehat{BOC}\). C. ![]() \(\widehat{BDC}\). D.
\(\widehat{BDC}\). D. ![]() \(\widehat{BEC}\).
\(\widehat{BEC}\).
Câu 4. Đường thẳng nào sau đây là trục đối xứng của đường tròn tâm ![]() \(O\) ?
\(O\) ?
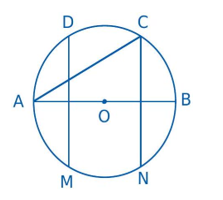
A.![]() \(CN\). B.
\(CN\). B.![]() \(AC\). C.
\(AC\). C.![]() \(DM\). D.
\(DM\). D.![]() \(AB\).
\(AB\).
Câu 5. Biểu thức nào sau đây là căn thức bậc ba của một biểu thức đại số?
A. ![]() \(\sqrt[3]{x} + 1\) B.
\(\sqrt[3]{x} + 1\) B. ![]() \(\sqrt[3]{x} + \sqrt{x} + 1\). C.
\(\sqrt[3]{x} + \sqrt{x} + 1\). C. ![]() \(\sqrt[3]{x} - 1\). D.
\(\sqrt[3]{x} - 1\). D. ![]() \(\sqrt[3]{x}\).
\(\sqrt[3]{x}\).
Câu 6. Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn?
A. ![]() \(\left\{ \begin{matrix}
x + y = 1 \\
x - y = 3.
\end{matrix} \right.\) B.
\(\left\{ \begin{matrix}
x + y = 1 \\
x - y = 3.
\end{matrix} \right.\) B. ![]() \(\left\{
\begin{matrix}
x + y = 3 \\
xy = 2
\end{matrix} \right.\) C.
\(\left\{
\begin{matrix}
x + y = 3 \\
xy = 2
\end{matrix} \right.\) C. ![]() \(\left\{ \begin{matrix}
xy = 4 \\
x - y = 3.
\end{matrix} \right.\) D.
\(\left\{ \begin{matrix}
xy = 4 \\
x - y = 3.
\end{matrix} \right.\) D. ![]() \(\left\{
\begin{matrix}
x^{2} + y^{2} = 2 \\
x + y = 2
\end{matrix} \right.\)
\(\left\{
\begin{matrix}
x^{2} + y^{2} = 2 \\
x + y = 2
\end{matrix} \right.\)
Câu 7. Cho hai số ![]() \(a,b\) được biểu diễn trên trục số (hình vẽ).
\(a,b\) được biểu diễn trên trục số (hình vẽ).
![]()
Phát biểu nào sau đây là đúng?
A. ![]() \(a < b\) và
\(a < b\) và ![]() \(b < 0\). B.
\(b < 0\). B. ![]() \(0 < b\) và
\(0 < b\) và ![]() \(b
< a\). C.
\(b
< a\). C. ![]() \(a < 0\) và
\(a < 0\) và ![]() \(0 < b\). D.
\(0 < b\). D. ![]() \(0 < a\) và
\(0 < a\) và ![]() \(a
< b\)
\(a
< b\)
Câu 8. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. ![]() \(x + y - 1 > 0\). B.
\(x + y - 1 > 0\). B. ![]() \(x - 1 > 0\). C.
\(x - 1 > 0\). C. ![]() \(x + y > 0\). D.
\(x + y > 0\). D. ![]() \(x - y > 0\).
\(x - y > 0\).
Câu 9. Điều kiện xác định của phương trình ![]() \(\frac{2x + 5}{2x} - \frac{x}{x + 5} = 0\) là:
\(\frac{2x + 5}{2x} - \frac{x}{x + 5} = 0\) là:
A. ![]() \(x \neq 0\) và
\(x \neq 0\) và ![]() \(x \geq - 5\). B.
\(x \geq - 5\). B. ![]() \(x \neq 0\) và
\(x \neq 0\) và ![]() \(x
\neq - 5\).
\(x
\neq - 5\).
C. ![]() \(x \neq \pm 5\). D.
\(x \neq \pm 5\). D. ![]() \(x \geq 0\) và
\(x \geq 0\) và ![]() \(x
\geq - 5\).
\(x
\geq - 5\).
Câu 10. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn?
A. ![]() \(\frac{1}{2}y^{2} + 5 \geq 0\). B.
\(\frac{1}{2}y^{2} + 5 \geq 0\). B. ![]() \(\frac{2}{y} - 3 > 0\). C.
\(\frac{2}{y} - 3 > 0\). C. ![]() \(3x - 9 > 0\). D.
\(3x - 9 > 0\). D. ![]() \(0.x - 6 < 0\).
\(0.x - 6 < 0\).
Câu 11. Cho bất đẳng thức ![]() \(2 \geq 3a -
1\). Bất đẳng thức nào cùng chiều với bất đẳng thức đã cho
\(2 \geq 3a -
1\). Bất đẳng thức nào cùng chiều với bất đẳng thức đã cho
A. ![]() \(4 < 2a\). B.
\(4 < 2a\). B. ![]() \(3a - 2 \leq 4\). C.
\(3a - 2 \leq 4\). C. ![]() \(2 = 3a - 1\). D.
\(2 = 3a - 1\). D. ![]() \(a - 1 \geq - 2\).
\(a - 1 \geq - 2\).
Câu 12. Cho ![]() \(\alpha;\beta\) là hai góc nhọn bất kì với
\(\alpha;\beta\) là hai góc nhọn bất kì với ![]() \(\alpha <
\beta\) khi đó:
\(\alpha <
\beta\) khi đó:
A. ![]() \(\sin\alpha > \sin\beta\) B.
\(\sin\alpha > \sin\beta\) B. ![]() \(\cos\alpha < \cos\beta\) C.
\(\cos\alpha < \cos\beta\) C. ![]() \(\tan\alpha < \tan\beta\) D.
\(\tan\alpha < \tan\beta\) D. ![]() \(\cot\alpha < \cot\beta\)
\(\cot\alpha < \cot\beta\)
Phần 2. Câu trắc nghiệm đúng sai (2 điểm)
Thí sinh trả lời câu 13 và câu 14. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh trả lời đúng hoặc sai.
Câu 13 (1 điểm): Bạn Dương có số tiền không quá ![]() \(70000\) đồng gồm
\(70000\) đồng gồm ![]() \(15\) tờ tiền mệnh giá
\(15\) tờ tiền mệnh giá ![]() \(2000\) đồng và
\(2000\) đồng và ![]() \(5000\) đồng. Hỏi bạn Dương có nhiều nhất bao nhiêu tờ tiền loại
\(5000\) đồng. Hỏi bạn Dương có nhiều nhất bao nhiêu tờ tiền loại ![]() \(5000\) đồng? Gọi số tờ tiền loại
\(5000\) đồng? Gọi số tờ tiền loại ![]() \(5000\) đồng là
\(5000\) đồng là ![]() \(x\) (với
\(x\) (với ![]() \(x\) nguyên dương).
\(x\) nguyên dương).
|
Phát biểu |
Đúng |
Sai |
|
a) Số tờ loại |
|
|
|
b) Số tờ loại |
|
|
|
c) Số tiền loại |
|
|
|
d) Bất phương trình thỏa mãn bài toán là: |
|
|
Câu 14 (1 điểm): Một chiếc máy bay, bay lên với vận tốc ![]() \(500km/h\). Đường bay lên tạo với phương nằm ngang một góc
\(500km/h\). Đường bay lên tạo với phương nằm ngang một góc ![]() \(30^{0}\).(như hình vẽ)
\(30^{0}\).(như hình vẽ)
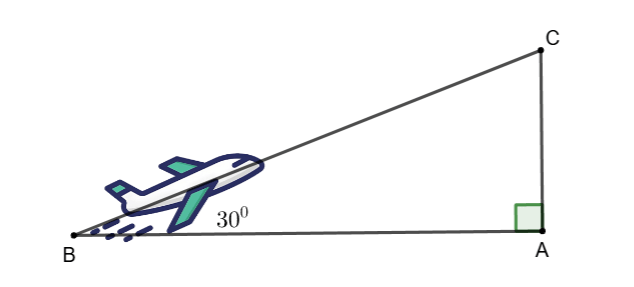
|
Phát biểu |
Đúng |
Sai |
|
a) |
|
|
|
b) |
|
|
|
c) |
|
|
|
d) Độ dài |
|
|
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn (2 điểm)
Trong mỗi câu hỏi từ 15 đến 18, hãy viết câu trả lời đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Câu 15. Rút gọn biểu thức: ![]() \(A = \sqrt{12}
- \frac{3 + \sqrt{3}}{\sqrt{3} + 1} + \frac{11}{2\sqrt{3} +
1}\)ta được kết quả là: …
\(A = \sqrt{12}
- \frac{3 + \sqrt{3}}{\sqrt{3} + 1} + \frac{11}{2\sqrt{3} +
1}\)ta được kết quả là: …
Câu 16. Giải bất phương trình sau ![]() \(4x + (x
+ 1) \geq 9x - (5x - 4)\)?
\(4x + (x
+ 1) \geq 9x - (5x - 4)\)?
Câu 17. Người ta giăng lưới để nuôi riêng một loại cá trên một góc hồ. Biết rằng lưới được giăng theo một đường thẳng từ một vị trí trên bờ ngang đến một vị trí trên bờ dọc và phải đi qua một cái cọc đã cắm sẵn ở vị trí A. Hỏi diện tích nhỏ nhất có thể giăng là bao nhiêu, biết rằng khoảng cách từ cọc đến bờ ngang là 5 m và khoảng cách từ cọc đến bờ dọc là 12 m.
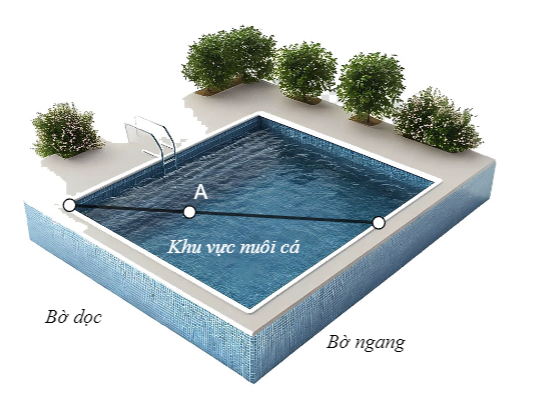
Câu 18. Một chất điểm chuyển động trên một đường tròn có bán kính ![]() \(r = 0,3\)m với tốc độ không đổi. Chất điểm chuyển động hết một vòng quanh đường tròn đó trong
\(r = 0,3\)m với tốc độ không đổi. Chất điểm chuyển động hết một vòng quanh đường tròn đó trong ![]() \(20\)s. Tính tốc độ của chất điểm (theo đơn vị mét trên giây và làm tròn kết quả đến hàng phần trăm).
\(20\)s. Tính tốc độ của chất điểm (theo đơn vị mét trên giây và làm tròn kết quả đến hàng phần trăm).
B. TỰ LUẬN (3 ĐIỂM)
Bài 1 (1 điểm). Rút gọn biểu thức sau:
![]() \(A = \left( \frac{\sqrt{y}}{x +
\sqrt{xy}} + \frac{\sqrt{y}}{x - \sqrt{xy}} \right):\frac{2\sqrt{y}}{x -
y}\ \ ;\ \ \ x > 0,\ \ y > 0,\ \ x \neq y\)
\(A = \left( \frac{\sqrt{y}}{x +
\sqrt{xy}} + \frac{\sqrt{y}}{x - \sqrt{xy}} \right):\frac{2\sqrt{y}}{x -
y}\ \ ;\ \ \ x > 0,\ \ y > 0,\ \ x \neq y\)
Bài 2 (1,5 điểm). Cho đường tròn ![]() \((O;R)\), điểm
\((O;R)\), điểm ![]() \(I\) nằm ngoài đường tròn,
\(I\) nằm ngoài đường tròn, ![]() \(IA,IB\) lần lượt tiếp xúc với đường tròn tại
\(IA,IB\) lần lượt tiếp xúc với đường tròn tại ![]() \(A,B\) và
\(A,B\) và ![]() \(\widehat{AIB} = 60^{\circ}\). Điểm
\(\widehat{AIB} = 60^{\circ}\). Điểm ![]() \(C\) thuộc cung nhỏ
\(C\) thuộc cung nhỏ ![]() \(AB\) của
\(AB\) của ![]() \((O;R)\),
\((O;R)\), ![]() \(C\) khác
\(C\) khác ![]() \(A\) và
\(A\) và ![]() \(B\). Tiếp tuyến tại
\(B\). Tiếp tuyến tại ![]() \(C\) của
\(C\) của ![]() \((O;R)\) cắt các cạnh
\((O;R)\) cắt các cạnh ![]() \(IA\) và
\(IA\) và ![]() \(IB\) lần lượt tại
\(IB\) lần lượt tại ![]() \(M\) và
\(M\) và ![]() \(N\).
\(N\).
a) So sánh ![]() \(\widehat{OIA}\) và
\(\widehat{OIA}\) và ![]() \(\widehat{OIB},IA\) và
\(\widehat{OIB},IA\) và ![]() \(IB\).
\(IB\).
b) Tính số đo góc ![]() \(OIA\) và tính theo
\(OIA\) và tính theo ![]() \(R\) độ dài đoạn các đoạn thẳng IA, IB.
\(R\) độ dài đoạn các đoạn thẳng IA, IB.
c) Chứng minh rằng ![]() \(\widehat{MON} =
60^{\circ}\).
\(\widehat{MON} =
60^{\circ}\).
Bài 3 (0,5 điểm). Một chiếc thuyền xuôi dòng và ngược dòng trên khúc sông dài 40 km hết 4 giờ 30 phút. Biết thời gian thuyền xuôi dòng 5 km bằng thời gian thuyền ngược dòng 4 km. Tính vận tốc dòng nước.
- Hết -
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.










