Chia đa thức cho đơn thức
Chuyên đề Toán học lớp 8: Chia đa thức cho đơn thức được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Chia đa thức cho đơn thức
A. Lý thuyết
1. Đa thức chia cho đơn thức.
Với A là đa thức và B là đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một biểu thức Q (Q có thể là đa thức hoặc đơn thức) sao cho A= B.Q.
Trong đó:
A là đa thức bị chia.
B là đơn thức chia.
Q là thương
Kí hiệu: Q= A : B hoặc
2. Quy tắc
Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B), ta chia mỗi hạng tử của A cho B rồi cộng các kết quả với nhau.
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, thường ta phân tích trước để rút gọn cho nhanh.
Ví dụ 1: Thực hiện phép tính
a, (12x4y3 + 8x3y2 - 4xy2):2xy.
b, (- 2x5 + 6x2 - 4x3):2x2
Hướng dẫn:
a) Ta có: (12x4y3 + 8x3y2 - 4xy2):2xy = (12x4y3:2xy) + (8x3y2:2xy) - (4xy2:2xy)
= 6x4 - 1.y3 - 1 + 4x3 - 1.y2 - 1 - 2x1 - 1.y2 - 1 = 6x3y2 + 4x2y - 2y
b) Ta có: (- 2x5 + 6x2 - 4x3):2x2 = (- 2x5:2x2) + (6x2:2x2) - (4x3:2x2)
= - x5 - 2 + 3x2 - 2 - 2x3 - 2 = - x3 - 2x + 3.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Đa thức M thỏa mãn xy2 + 1/3x2y2 + 7/2x3y = (5xy).M là?
A. M = y + 1/15xy2 + 7/10x2
B. M = 1/5y + 1/15xy + 7/10x2
C. M = - 1/5y + 1/5x2y + 7/10x2
D. Cả A, B, C đều sai.
Ta có xy2 + 1/3x2y2 + 7/2x3y = (5xy).M
⇒ M = (xy2 + 1/3x2y2 + 7/2x3y):(5xy)
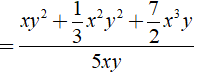= 1/5y + 1/15xy + 7/10x2.
Chọn đáp án B.
Bài 2: Kết quả nào sau đây đúng?
A. (- 3x3 + 5x2y - 2x2y2):(- 2) = - 3/2x3 - 5/2x2y + x2y2
B. (3x3 - x2y + 5xy2):(1/2x) = 6x2 - 2xy + 10y2
C. (2x4 - x3 + 3x2):(- 1/3x) = 6x2 + 3x - 9
D. (15x2 - 12x2y2 + 6xy3):(3xy) = 5x - 4xy - 2y2
Ta có:
+ (- 3x3 + 5x2y - 2x2y2):(- 2) = 3/2x3 - 5/2x2y + x2y2
⇒ Đáp án A sai.
+ (3x3 - x2y + 5xy2):(1/2x) = 6x2 - 2xy + 10y2
⇒ Đáp án B đúng.
+ (2x4 - x3 + 3x2):(- 1/3x) = - 6x3 + 3x2 - 9x
⇒ Đáp án C sai.
+ (15x2 - 12x2y2 + 6xy3):(3xy) = 5x/y - 4xy - 2y2
⇒ Đáp án D sai.
Chọn đáp án B.
Bài 3: Giá trị của biểu thức A = [(x - y)5 + (x - y)4 + (x - y)3]:(x - y) với x = 3, y = 1 là?
A. A =28 B. A =16 C. A =20 D. A =14
Ta có A = [(x - y)5 + (x - y)4 + (x - y)3]:(x - y)
= (x - y)4 + (x - y)3 + (x - y)2
Với x = 3, y = 1 ta có A = (3 - 1)4 + (3 - 1)3 + (3 - 1)2 = 24 + 23 + 22 = 16 + 8 + 4 = 28.
Chọn đáp án A.
II. Bài tập tự luận
Bài 1: Thực hiện các phép tính sau:
a, (1/2a2x4 + 4/3ax3 - 2/3ax2):(- 2/3ax2)
b, 4(3/4x - 1) + (12x2 - 3x):(- 3x) - (2x + 1)
Hướng dẫn:
a) Ta có: (1/2a2x4 + 4/3ax3 - 2/3ax2):(- 2/3ax2)
= (1/2a2x4: - 2/3ax2) + (4/3ax3: - 2/3ax2) + (- 2/3ax2: - 2/3ax2)
= - 3/4ax2 - 2x + 1
b) Ta có 4(3/4x - 1) + (12x2 - 3x):(- 3x ) - (2x + 1)
= 4(3/4x - 1) + [(12x2: - 3x) + (- 3x: - 3x)] - (2x + 1)
= 4(3/4x - 1) + (- 4x + 1) - (2x + 1) = 3x - 4 + 1 - 4x - 2x - 1 = - 3x - 4
Bài 2: Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7xn - 1y5 - 5x3y4;
B = 5x2yn
Hướng dẫn:
Ta có A:B = (7xn - 1 y5 - 5x3y4):(5x2yn) = 7/5xn - 3 y5 - n - xy4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
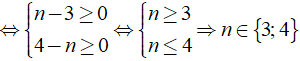
Vậy giá trị n cần tìm là n∈{3; 4}
Bài 3: Tìm đa thức A biết
a, A.6x4 = 24x9 - 30x8 + 1/2x5
b, A.(- 5/2x3y2) = 5x6y4 + 15/2x5y3 - 10x3y2
Hướng dẫn:
a) Ta có A.6x4 = 24x9 - 30x8 + 1/2x5 ⇒ A = (24x9 - 30x8 + 1/2x5):(6x4)
⇔ A = 24/6x9 - 4 - 30/6x8 - 4 + 1/12x5 - 4 = 4x5 - 5x4 + 1/12x
Vậy A = 4x5 - 5x4 + 1/12x.
b) Ta có A.(- 5/2x3y2) = 5x6y4 + 15/2x5y3 - 10x3y2 ⇒ A = (5x6y4 + 15/2x5y3 - 10x3y2):(- 5/2x3y2)
⇔ A = - 2x6 - 3y4 - 2 - 3x5 - 3y3 - 2 + 4x3 - 3y2 - 2
Vậy A = - 2x3y2 - 3x2y + 1.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Chia đa thức cho đơn thức. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
