Toán lớp 6 bài 6 sách mới

Giải Toán lớp 6 Kết nối tri thức, Cánh Diều, Chân trời sáng tạo

Toán lớp 6 bài 6

Giải Toán lớp 6 bài 6 của 3 bộ sách mới: Kết nối tri thức, Cánh Diều, Chân trời sáng tạo với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 6. Lời giải bài tập Toán 6 bài Ôn tập và bổ túc về số tự nhiên với các bài giải tương ứng với từng bài học trong sách giúp cho các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán và để học tốt Toán lớp 6.

1. Giải Toán lớp 6 bài 6 sách Kết nối tri thức với cuộc sống

Lũy thừa với số mũ tự nhiên Kết nối tri thức lớp 6 trang 17, 18, 19 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học Toán 6 sách mới, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách KNTT. Tham khảo chi tiết: Toán lớp 6 bài 6 Lũy thừa với số mũ tự nhiên Kết nối tri thức.

Toán lớp 6 tập 1 trang 24 Câu 1.36

Viết các tích sau dưới dạng một lũy thừa:

a) 9 . 9 . 9 . 9 . 9

b) 10 . 10 . 10 . 10

c) 5 . 5 . 5 . 25

c) a . a . a . a . a . a

Đáp án

a) 9 . 9 . 9 . 9 . 9 = 9 ⁵

b) 10 . 10 . 10 . 10 = 10⁴

c) 5 . 5 . 5 . 25 = 5 . 5 . 5 . 5 . 5 = 5⁵

c) a . a . a . a . a . a = a⁶

Toán lớp 6 tập 1 trang 24 Câu 1.37

Hoàn thành bảng sau vào vở:

Lũy thừa	Cơ số	Số mũ	Giá trị của lũy thừa
4 ³	?	?	?
?	3	5	?
?	2	?	128

Đáp án

Lũy thừa	Cơ số	Số mũ	Giá trị của lũy thừa
4³	4	3	64
3⁵	3	5	243
2⁷	2	7	128

Toán lớp 6 tập 1 trang 24 Câu 1.38

Tính:

a) 2 ⁵

b) 3 ³

c) 5 ²

d) 10 ⁹

Đáp án

a. ${2^5} = 2.2.2.2.2 = 32$ ${2^5} = 2.2.2.2.2 = 32$

b. ${3^3} = 3.3.3 = 27$ ${3^3} = 3.3.3 = 27$

c. ${5^2} = 5.5 = 25$ ${5^2} = 5.5 = 25$

d. ${10^9} = \underbrace {10.10.10.....10}_9 = 1000000000$ ${10^9} = \underbrace {10.10.10.....10}_9 = 1000000000$

Toán lớp 6 tập 1 trang 24 Câu 1.39

Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các lũy thừa của 10: 215; 902; 2 020; 883 001

Đáp án

Ta có:

$\begin{matrix} 215 = 200 + 10 + 5 = {2.10^2} + {10^1} + 5 \hfill \\ 902 = 900 + 2 = 9.100 + 2 = {9.10^2} + 2 \hfill \\ 2020 = 2.1000 + 2.10 = {2.10^3} + {2.10^1} \hfill \\ 883001 = 800000 + 80000 + 3000 + 1 = {8.10^5} + {8.10^4} + {3.10^3} + 1 \hfill \\ \end{matrix}$ $\begin{matrix} 215 = 200 + 10 + 5 = {2.10^2} + {10^1} + 5 \hfill \\ 902 = 900 + 2 = 9.100 + 2 = {9.10^2} + 2 \hfill \\ 2020 = 2.1000 + 2.10 = {2.10^3} + {2.10^1} \hfill \\ 883001 = 800000 + 80000 + 3000 + 1 = {8.10^5} + {8.10^4} + {3.10^3} + 1 \hfill \\ \end{matrix}$

Toán lớp 6 tập 1 trang 24 Câu 1.40

Tính 11 ² , 111 ² . Từ đó hãy dự đoán kết quả của 1111 ²

Đáp án

Ta có:

$\begin{matrix} {11^2} = 11.11 = 121 \hfill \\ {111^2} = 111.111 = 12321 \hfill \\ \end{matrix}$ $\begin{matrix} {11^2} = 11.11 = 121 \hfill \\ {111^2} = 111.111 = 12321 \hfill \\ \end{matrix}$

Dự đoán ${1111^2} = 1234321$ ${1111^2} = 1234321$

Kiểm tra kết quả ${1111^2} = 1111.1111 = 1234321$ ${1111^2} = 1111.1111 = 1234321$

Toán lớp 6 tập 1 trang 24 Câu 1.41

Biết 2 ¹⁰ = 1024 . Hãy tính 2 ⁹ và 2 ¹¹

Đáp án

Ta có:

$\begin{matrix} {2^{10}} = {2^{9 + 1}} = {2^9}{.2^1} = {2^9}.2 = 1024 \hfill \\ \Rightarrow {2^9} = 1024:2 = 512 \hfill \\ \end{matrix}$ $\begin{matrix} {2^{10}} = {2^{9 + 1}} = {2^9}{.2^1} = {2^9}.2 = 1024 \hfill \\ \Rightarrow {2^9} = 1024:2 = 512 \hfill \\ \end{matrix}$

Ta lại có:

$\begin{matrix} {2^{10}} = {2^{11 - 1}} = {2^{11}}:{2^1} = {2^{11}}:2 = 1024 \hfill \\ \Rightarrow {2^{11}} = 1024.2 = 2048 \hfill \\ \end{matrix}$ $\begin{matrix} {2^{10}} = {2^{11 - 1}} = {2^{11}}:{2^1} = {2^{11}}:2 = 1024 \hfill \\ \Rightarrow {2^{11}} = 1024.2 = 2048 \hfill \\ \end{matrix}$

Toán lớp 6 tập 1 trang 24 Câu 1.42

Tính :

a) 5 ⁷ .5 ³

b) 5 ⁸ : 5 ⁴

Đáp án

a. ${5^7}{.5^3} = {5^{7 + 3}} = {5^{10}}$ ${5^7}{.5^3} = {5^{7 + 3}} = {5^{10}}$

b. ${5^8}:{5^4} = {5^{8 - 4}} = {5^4}$ ${5^8}:{5^4} = {5^{8 - 4}} = {5^4}$

Toán lớp 6 tập 1 trang 24 Câu 1.43

Ta có: 1 + 3 + 5 = 9 = 3 ²

Viết các tổng sau dưới dạng bình phương của một số tự nhiên:

a) 1 + 3 + 5 + 7

b) 1 + 3 + 5 + 7 + 9

Đáp án

a. 1 + 3 + 5 + 7 = 16 = 4²

b. 1 + 3 + 5 + 7 + 9 = 25 = 5²

Toán lớp 6 tập 1 trang 24 Câu 1.44

Trái Đất có khối lượng khoảng 60.10 ²⁰ tấn. Mỗi giây Mặt Trời tiêu thụ 6.10 ⁶ tấn khí Hydrogen (theo vnexpress.net). Hỏi Mặt Trời cần bao nhiêu giây để tiêu thụ một lượng khí hdrogen có khối lượng bằng khối lượng Trái Đất?

Đáp án

Thời gian để Mặt Trời tiêu thụ một lượng khí hdrogen có khối lượng bằng khối lượng Trái Đất là:

$\left( {{{60.10}^{20}}} \right):\left( {{{6.10}^6}} \right) = \frac{{60}}{6}{.10^{20 - 6}} = {10.10^{14}} = {10^{1 + 14}} = {10^{15}}\left( s \right)$ $\left( {{{60.10}^{20}}} \right):\left( {{{6.10}^6}} \right) = \frac{{60}}{6}{.10^{20 - 6}} = {10.10^{14}} = {10^{1 + 14}} = {10^{15}}\left( s \right)$

Toán lớp 6 tập 1 trang 24 Câu 1.45

Theo các nhà khoa học, mỗi giây cơ thể con người trung bình tạo ra khoảng 25.10 ⁵ tế bào hồng cầu (theo www.healthline.com). Hãy tính xem mỗi giờ có bao nhiêu tế bào hồng cầu được tạo ra?

Đáp án

Đổi 1 giờ = 3600 giây

Mỗi giờ số tế bào hồng cầu được tạo ra là:

${25.10^5}.3600 = {90000.10^5} =9.10^4 .10^5=9.10^{4+5}=9.10^9$ ${25.10^5}.3600 = {90000.10^5} =9.10^4 .10^5=9.10^{4+5}=9.10^9$ (tế bào)

2. Giải Toán lớp 6 bài 6 sách Chân trời sáng tạo

Giải Chia hết và chia có dư. Tính chất chia hết của một tổng Chân trời sáng tạo lớp 6 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học bài 6 Toán 6 trang 21, 22, 23 giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách Chân trời sáng tạo. Xem chi tiết: Giải Toán lớp 6 bài 6 Chia hết và chia có dư. Tính chất chia hết của một tổng

3. Giải Toán lớp 6 bài 6 sách Cánh Diều

Giải Thứ tự thực hiện các phép tính Cánh Diều lớp 6 bao gồm đáp án chi tiết cho từng phần, từng bài tập trong nội dung chương trình học bài 6 Toán 6 trang 26, 27, 28, 29, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 6 sách Cánh Diều. Xem chi tiết: Toán lớp 6 bài 5 Phép tính lũy thừa với số mũ tự nhiên Cánh Diều

4. Giải Toán lớp 6 bài 6 sách cũ

Tóm tắt kiến thức phép trừ và phép chia lớp 6

1. Cho hai số tự nhiên a và b. Nếu có số tự nhiên x mà b + x = a thì ta có phép trừ a – b = x. Số a gọi là số bị trừ, số b là số trừ, số x là hiệu số.

Lưu ý:

Nếu b + x = a thì x = a – b và b = a – x.
Nếu x = a – b thì b + x = a và b = a – x.
Điều kiện để thực hiện được phép trừ là số bị trừ phải lớn hơn hay bằng số trừ.

2. Cho hai số tự nhiên a và b, với b ≠ 0. Nếu có số tự nhiên x mà b . x = a thì ta có phép chia hết a : b = x. Số a gọi là số bị chia, số b là số chia, số x là thương.

Lưu ý:

Nếu b . x = a thì x = a : b nếu b ≠ 0 và b = a : x nếu x ≠ 0.
Nếu x = a : b thì b . x = a và nếu a ≠ 0 thì b = a : x.

3. Cho hai số tự nhiên a và b, với b ≠ 0, ta luôn tìm được hai số tự nhiên q và r sao cho a = bq + r, trong đó 0 ≤ r < b.

Khi r ≠ 0 ta nói rằng ta có phép chia có dư với a là số bị chia, b là số chia, q là thương, r là số dư.

4. Số chia bao giờ cũng khác 0.

Câu hỏi 1 SGK Toán 6 trang 21 tập 1

Điền vào chỗ trống:

a) a – a = …;

b) a – 0 = …;

c) Điều kiện để có hiệu a – b là …

Lời giải chi tiết

Ta có:

a) a – a = 0

b) a – 0 = a

c) Điều kiện để có hiệu a – b là a > b

Câu hỏi 2 SGK Toán 6 trang 21 tập 1

Điền vào chỗ trống:

a) 0 : a=…(a≠0);

b) a : a=…(a≠0);

c) a : 1=…

Phương pháp giải

Sử dụng:

+) 0 chia số nào cũng bằng 0

+) Số nào chia cho 1 cũng bằng chính nó.

Lời giải chi tiết

Ta có:

a) 0 : a = 0 (a≠0)

b) a : a = 1 (a≠0)

c) a : 1 = a

Câu hỏi 3 SGK Toán 6 trang 22 tập 1

Điền vào ô trống ở các trường hợp có thể xảy ra:

Số bị chia	600	1312	15
Số chia	17	32	0	13
Thương				4
Số dư				15
	(1)	(2)	(3)	(4)

Phương pháp giải

Thực hiện phép chia hai số tự nhiên rồi điền vào ô trống.

Lời giải chi tiết

Ta có kí hiệu như sau: Số bị chia là a; Số chia là b; Thương là q; Số dư là r.

- Ở cột (1) ta có a = 600; b = 17

Chia 600 cho 17 được q = 35 ; r = 5

- Ở cột (2) ta có a = 1312 ; b = 32

Chia 1312 cho 32 được q = 41 ; r = 0

- Ở cột (3) ta có a = 15 ; b = 0

Có b = 0 nên phép chia a cho b không thể thực hiện được

- Ở cột (4) ta có b = 13 ; q = 5 ; r = 2

Vậy a = b . q + r = 13 . 5 + 2 = 67

Ta có bảng:

Số bị chia	600	1312	15	67
Số chia	17	32	0	13
Thương	35	41		5
Số dư	5	0		2

Giải bài tập Toán lớp 6 SGK Trang 22, 23, 24 tập 1 - Phép trừ và phép chia

Giải Toán SGK Đại số 6 tập 1 trang 22 Bài 41

Hà Nội, Huế, Nha Trang, Thành phố Hồ Chí Minh nằm trên quốc lộ 1 theo thứ tự như trên. Cho biết các quãng đường trên quốc lộ ấy:

Hà Nội – Huế: 658km,

Hà Nội – Nha Trang: 1278km,

Hà Nội – Thành phố Hồ Chí Minh: 1710km.

Tính các quãng đường: Huế – Nha Trang, Nha Trang – Thành phố Hồ Chí Minh.

Phương pháp giải

Quãng đường từ Huế đến Nha Trang chính bằng quãng đường từ Hà Nội đến Nha Trang trừ đi quãng đường từ Hà Nội đến Huế.

Quãng đường từ Nha Trang đến TP HCM bằng quãng đường từ hà nội đến TP HCM trừ đi quãng đường từ HN đến Nha Trang

Đáp án và bài giải:

Quãng đường Huế – Nha Trang: 1278 – 658 = 620 (km).

Nha Trang – Thành phố Hồ Chí Minh: 1710 – 1278 = 432 (km).

Giải Toán SGK Đại số 6 tập 1 trang 23 Bài 42

Các số liệu về kênh đào Xuy-ê (Ai Cập) nối Địa Trung Hải và Hồng Hải được cho trong bảng 1 và bảng 2.

Bảng 1

Kênh đào Xuy-ê	Năm 1869	Năm 1955
Chiều rộng mặt kênh	58m	135m
Chiều rộng đáy kênh	22m	50m
Độ sâu của kênh	6m	13m
Thời gian tàu qua kênh	48 giờ	14 giờ

Bảng 2

Hành trình	Qua mũi Hảo Vọng	Qua kênh Xuy-ê
Luân Đôn - Bom-bay	17400km	10100km
Mác-xây- Bom-bay	16000km	7400km
Ô-đét-xa- Bom-bay	19000km	6800km

a) Trong bảng 1, các số liệu ở năm 1955 tăng thêm (hay giảm bớt) bao nhiêu so với năm 1869 (năm khánh thành kênh đào)?
b) Nhờ đi qua kênh đào Xuy-ê, mỗi hành trình trong bảng 2 giảm bớt được bao nhiêu kilômét?

Đáp án và bài giải:

Chiều rộng mặt kênh tăng lên 77m.

Chiều rộng đáy kênh tăng lên 28m.

Độ sâu của kênh tăng lên 7m.

Thời gian tàu qua kênh giảm bớt 34 giờ.

Hành trình Luân Đôn – Bom-bay giảm bớt 7300km.

Hành trình Mác-xây – Bom-bay giảm bớt 8600km.

Hành trình Ô-đét-xa – Bom-bay giảm bớt 12200km.

Kênh đào Xuy-ê	Năm 1869	Năm 1955
Chiều rộng mặt kênh	58m	135m
Chiều rộng đáy kênh	22m	50m
Độ sâu của kênh	6m	13m
Thời gian tàu qua kênh	48 giờ	14 giờ

Giải Toán SGK Đại số 6 tập 1 trang 23 Bài 43

Tính khối lượng của quả bí ở hình 18 khi cân thăng bằng:

Bài tập môn toán lớp 6 học kì 1

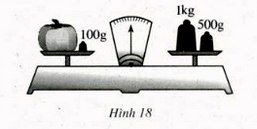
Bài giải:

Vận dụng điều lưu ý trong phần tóm tắt kiến thức.

Theo hình vẽ: Khối lượng quả bí + 100g = 1500g. Do đó khối lượng của quả bí là 1500g – 100g = 1400g.

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 44

Tìm số tự nhiên x, biết:

a) x : 13 = 41; b) 1428 : x = 14; c) 4x : 17 = 0;

d) 7x – 8 = 713; e) 8(x – 3) = 0; g) 0 : x = 0.

Đáp án và hướng dẫn giải:

Vận dụng điều lưu ý trong phần tóm tắt kiến thức.

a) Nếu x : 13 = 41 thì x = 41 . 13 = 533.

b) Nếu 1428 : x = 14 thì x = 1428 : 14 = 102.

c) Nếu 4x : 17 = 0 thì x = 0.

d) 7x – 8 = 713 thì 7x = 713 + 8 = 721. Do đó x = 721 : 7 = 103.

e) Nếu 8(x – 3) = 0 thì x – 3 = 0. Do đó x = 3.

g) Vì x là số chia nên x ≠ 0. Từ 0 : x = 0 suy ra x . 0 = 0. Vì mọi số nhân với 0 đều bằng 0 nên x là một số tự nhiên bất kì, khác 0.

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 45

Điền vào ô trống sao cho a = b.q + r với 0 ≤ r < b:

Đáp án:

a	392	278	357	b	420
b	28	13	21	14	35
q	14	21	17	25	12
r	0	5	0	10	0

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 46

a) Trong phép chia cho 2, số dư có thể bằng 0 hoặc 1. Trong mỗi phép chia cho 3, cho 4, cho 5, số dư có thể bằng bao nhiêu?

b) Dạng tổng quát của số chia hết cho 2 là 2k, dạng tổng quát của số chia hết cho 2 dư 1 là 2k + 1 với k ∈ N. Hãy viết dạng tổng quát của số chia hết cho 3, số chia hết cho 3 dư 1, số chia hết cho 3 dư 2.

Đáp án và hướng dẫn giải:

a) Số dư trong phép chia một số tự nhiên cho số tự nhiên b ≠ 0 là một số tự nhiên r < b nghĩa là r có thể là 0; 1;...; b – 1.

Số dư trong phép chia cho 3 có thể là 0; 1; 2.

Số dư trong phép chia cho 4 có thể là: 0; 1; 2; 3.

Số dư trong phép chia cho 5 có thể là: 0; 1; 2; 3; 4.

b) Dạng tổng quát của số tự nhiên chia hết cho 3 là 3k, với k ∈ N.

Dạng tổng quát của số tự nhiên chia hết cho 3, dư 1 là 3k + 1, với k ∈ N.

Dạng tổng quát của số tự nhiên chia hết cho 3, dư 2 là 3k + 2, với k ∈ N.

Giải bài tập Toán lớp 6 SGK Trang 24 tập 1 - Luyện tập Phép trừ và phép chia

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 47

Tìm số tự nhiên x, biết

a) (x – 35) – 120 = 0;

b) 124 + (118 – x) = 217;

c) 156 – (x + 61) = 82.

Đáp án và hướng dẫn giải:

a) (x-35) -120 = 0

x-35 = 0 +120

x-35 = 120

x = 120 +35

x = 155

b) 124 + (118 - x) = 217

118 – x = 217-124

118 – x = 93

x = 118 – 93

x = 25

c) 156 - (x + 61) = 82

x + 61 = 156 -82

x + 61 = 74

x = 74- 61

x = 13

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 48

Tính nhẩm bằng cách thêm vào ở số hạng này, bớt đi ở số hạng kia cùng một số thích hợp:

Ví dụ: 57 + 96 = (57 – 4) + (96 + 4) = 53 + 100 = 153.

Hãy tính nhẩm: 35 + 98; 46 + 29.

Đáp án và hướng dẫn giải:

35 + 98 = (35 – 2) + (98 + 2) = 33 + 100 = 133.

46 + 29 = (46 – 1) + (29 + 1) = 45 + 30 = 75.

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 49

Tính nhẩm bằng cách thêm vào số bị trừ và số trừ cùng một số thích hợp:

Ví dụ: 135 – 98 = (135 + 2) – (98 + 2) = 137 – 100 = 37.

Hãy tính nhẩm: 321 – 96; 1354 – 997.

Đáp án và hướng dẫn giải:

321 – 96 = (321 + 4) – (96 + 4) = 325 -100 = 225.

1354 – 997 = (1354 + 3) – (997 + 3) = 1357 – 1000 = 357.

Giải Toán SGK Đại số 6 tập 1 trang 24 Bài 50

Sử dụng máy tính bỏ túi:để tính:

425 – 257; 91 – 56; 82 – 56; 73 – 56; 652 – 46 – 46 – 46.

Đáp án

425 - 257 = 168;

91 - 56 = 35;

82 - 56 = 26;

73 - 56 = 17;

652 - 46 - 46 - 46 = 514.

Ngoài ra các em học sinh có thể tham khảo các bài giải SGK môn Toán lớp 6, Môn Ngữ văn 6, Môn Vật lý 6, môn Sinh Học 6, Lịch sử 6, Địa lý 6....và các đề thi học kì 1 lớp 6 và đề thi học kì 2 lớp 6 để chuẩn bị cho các bài thi đề thi học kì đạt kết quả cao.

Tham khảo các dạng Toán lớp 6:

Chia sẻ, đánh giá bài viết

123

30.283

Bài trước

Bài sau

Chia sẻ bởi:
Khang Anh
Nhóm:
Sưu tầm
Ngày: 23/09/2021

Tải về

Chọn file muốn tải về: