Toán lớp 3 trang 36 Luyện tập
Toán lớp 3 trang 36 Luyện tập với lời giải chi tiết giúp các em học sinh hiểu được cách lập bảng chia 7 và học thuộc bảng chia 7, cách thực hành chia trong phạm vi 7 và giải các bài toán có lời văn lớp 3.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 3, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 3 sau: Nhóm Tài liệu học tập lớp 3. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Giải Toán lớp 3 trang 36:
Toán lớp 3 trang 36 bài 1
Tính nhẩm:
| a) 7 × 8 = | 7 × 9 = | 7 × 6 = | 7 × 7 = |
| 56 : 7 = | 63 : 7 = | 42 : 7 = | 49 : 7 = |
| b) 70 : 7 = | 28 : 7 = | 30 : 6 = | 18 : 2 = |
| 63 : 7 = | 42 : 6 = | 35 : 5 = | 27 : 3 = |
| 14 : 7 = | 42 : 7 = | 35 : 7 = | 56 : 7 = |
Hướng dẫn giải
| a) 7 × 8 = 56 | 7 × 9 = 63 | 7 × 6 = 42 | 7 × 7 = 49 |
| 56 : 7 = 8 | 63 : 7 = 9 | 42 : 7 = 6 | 49 : 7 = 7 |
| b) 70 : 7 = 10 | 28 : 7 = 4 | 30 : 6 = 5 | 18 : 2 = 6 |
| 63 : 7 = 9 | 42 : 6 = 7 | 35 : 5 = 7 | 27 : 3 = 9 |
| 14 : 7 = 2 | 42 : 7 = 6 | 35 : 7 = 5 | 56 : 7 = 8 |
Toán lớp 3 trang 36 bài 2
\(\left. \begin{align} & \begin{matrix} 28 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 35 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 21 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 14 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 42 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 42 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{6}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 25 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{5}{{}} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix} 49 \end{matrix} \\ & \, \\ \end{align} \right|\begin{matrix} \dfrac{7}{{}} \\ \end{matrix}\)
Hướng dẫn giải:
\(\left. \begin{align} & \begin{matrix}28 \\ 28 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{4} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}35 \\ 35 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{5} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}21 \\ 21 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{3} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}14 \\ 14 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{2} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}42 \\ 42 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{6} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}42 \\ 42 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{6}{7} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}25 \\ 25 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{5}{5} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
\(\left. \begin{align} & \begin{matrix}49 \\ 49 \\ \end{matrix} \\ & \overline{\begin{align} &\,\,\, 0 \\ \end{align}} \\ \end{align} \right|\begin{matrix} \dfrac{7}{7} \\ \begin{matrix} \end{matrix} {} \\ \end{matrix}\)
Toán lớp 3 trang 36 bài 3
Cô giáo chia 35 học sinh thành các nhóm, mỗi nhóm có 7 học sinh. Hỏi chia được bao nhiêu nhóm?
Hướng dẫn giải
Số nhóm được chia là:
35 : 7 = 5 (nhóm)
Đáp số: 5 nhóm
Toán lớp 3 trang 36 bài 4
Tìm \(\frac{1}{7}\) số con mèo trong mỗi hình sau:
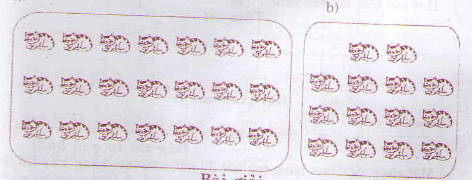
Hướng dẫn giải
C1: Trong hình vẽ có 7 cột, mỗi cột có 3 con mèo, như vậy \(\frac{1}{7}\) số con mèo là số con mèo trong 1 cột, tức là có 3 con mèo.
C2: Đếm tổng cộng có 21 con mèo
Vậy \(\frac{1}{7}\) số con mèo trong hình a là:
21 : 7 = 3 (con).
Đáp số: 3 con
b) 2 con mèo
>> Bài tiếp theo: Giải bài tập trang 37, 38 SGK Toán 3: Giảm đi một số lần
Trên đây là: Toán lớp 3 trang 36 Luyện tập. Trong quá trình học lớp 3, các em học sinh không tránh được việc gặp những bài toán 3 khó, nâng cao. Những bài tập sách giáo khoa cũng có thể khiến các em gặp khó khăn trong quá trình giải. Tuy nhiên, để cùng các em học Toán lớp 3 hiệu quả hơn, VnDoc cung cấp lời giải bài tập Toán 3 để các em tham khảo. Chúc các em học tốt và đạt kết quả cao.
