Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 (cũ)
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề thi học kì 1 Toán 12 Đề 1

Mô tả thêm:

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 12 nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 50 câu
  • Số điểm tối đa: 50 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
  • Câu 1: Thông hiểu

    Thu gọn biểu thức lũy thừa

    Với a là một số thực dương thì biểu thức P = \frac{{{a^{\sqrt 7 + 1}}.{a^{2 - \sqrt 7 }}}}{{{{\left( {{a^{\sqrt 2 - 2}}} ight)}^{\sqrt 2 + 2}}}} được rút gọn là:

    Ta có: P = \frac{{{a^{\sqrt 7 + 1}}.{a^{2 - \sqrt 7 }}}}{{{{\left( {{a^{\sqrt 2 - 2}}} ight)}^{\sqrt 2 + 2}}}} = \frac{{{a^3}}}{{{a^{ - 2}}}} = {a^5}

  • Câu 2: Nhận biết

    Đếm số hình đa diện

    Cho các hình sau:

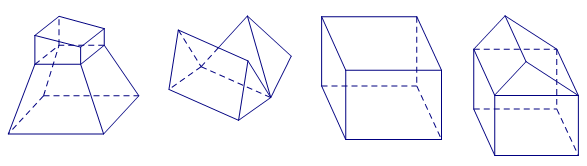
    Đếm số hình đa diện

    Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:

     Các hình đa diện là:

    Đếm số hình đa diện; Đếm số hình đa diện; Đếm số hình đa diện

  • Câu 3: Thông hiểu

    Tính đường kính của mặt cầu

    Cho các điểm A(2;4; - 1) và B(0; - 2;1) và đường thẳng d:\left\{ \begin{matrix} x = 1 + 2t \\ y = 2 - t \\ z = 1 + t \\ \end{matrix} \right.. Gọi (S) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Đường kính mặt cầu (S) bằng:

    Gọi I(1 + 2t;2 - t;1 + t) trên d vì IA = IB \Rightarrow t = 1 \Rightarrow R = IA = \sqrt{19} đường kính là 2\sqrt{19}.

  • Câu 4: Vận dụng

    Chọn đáp án đúng

    Cho hàm số y = f(x) có đạo hàm f'(x) = x^{2}(x - 9)(x - 4)^{2}. Khi đó hàm số y = f\left( x^{2} ight) nghịch biến trên khoảng nào?

    Ta có:

    y' = \left( f\left( x^{2} ight) ight)' = 2x.f'\left( x^{2} ight) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x^{4}\left( x^{2} - 9 ight)\left( x^{2} - 4 ight)^{2} = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = \pm 3 \\ x = \pm 2 \\ \end{matrix} ight.

    Ta có bảng biến thiên:

    Dựa vào bảng biến thiên ta có hàm số nghịch biến trên ( - \infty; - 3) và (0;3).

  • Câu 5: Nhận biết

    Tìm cực đại của hàm số

    Cho hàm số y = f(x) có đạo hàm f'(x) = x(x - 1)(x - 2);\forall x\mathbb{\in R}. Tìm số điểm cực đại của hàm số đã cho.

    Ta có: f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ x = 2 \\ \end{matrix} ight.

    Ta có bảng xét dấu:

    Suy ra hàm số có một điểm cực đại.

  • Câu 6: Vận dụng cao

    Tính thể tích đa diện

    Cho khối lăng trụ ABC.A'B'C'có thể tích bằng 60 \,\text{cm}^3, các điểm M, N, P lần lượt thuộc các cạnh AA',BB',CC' sao cho AM = 2MA',BN = 3NB',CP = 4PC'. Thể tích của khối đa diện BC.MNP là bao nhiêu? (Đơn vị: cm^3)

    31 || 31 cm^3 || ba mươi mốt xăng ti mét khối || Ba mươi mốt xăng ti mét khối

    Đáp án là:

    Cho khối lăng trụ ABC.A'B'C'có thể tích bằng 60 \,\text{cm}^3, các điểm M, N, P lần lượt thuộc các cạnh AA',BB',CC' sao cho AM = 2MA',BN = 3NB',CP = 4PC'. Thể tích của khối đa diện BC.MNP là bao nhiêu? (Đơn vị: cm^3)

    31 || 31 cm^3 || ba mươi mốt xăng ti mét khối || Ba mươi mốt xăng ti mét khối

     

    Ta có   MA = 2MA' \Rightarrow \frac{{AM}}{{AA'}} = \frac{2}{3};

               BN = 3NB' \Rightarrow \frac{{BN}}{{BB'}} = \frac{3}{4};

               CP = 4PC' \Rightarrow \frac{{CP}}{{CC'}} = \frac{4}{5}

    Nên \dfrac{{{V_{ABCMNP}}}}{{{V_{ABCA'B'C'}}}} = \frac{{\dfrac{2}{3} + \dfrac{3}{4} + \dfrac{4}{5}}}{3} = \dfrac{{133}}{{180}} \Rightarrow {V_{ABCMNP}} = \dfrac{{133}}{{180}}.60 = \dfrac{{133}}{3}

    Mà  {V_{M.ABC}} = \frac{1}{3}d\left( {M;\left( {ABC} ight)} ight).{S_{ABC}}

         = \frac{1}{3}.\frac{2}{3}d\left( {A';\left( {ABC} ight)} ight).{S_{ABC}} = \frac{2}{9}.{V_{ABC.A'B'C'}} = \frac{{40}}{3}.

    Vậy {V_{BCMNP}} = \frac{{133}}{3} - \frac{{40}}{3} = 31\left( {c{m^3}} ight).

  • Câu 7: Thông hiểu

    Tìm tham số m thỏa mãn yêu cầu

    Gọi m là giá trị nhỏ nhất của hàm số y = x + \frac{4}{x} trên khoảng (0; + \infty). Tìm m.

    Cách 1:

    Hàm số y = x + \frac{4}{x} liên tục và xác định trên (0; + \infty).

    Ta có

    y' = 1 - \frac{4}{x^{2}} = \frac{x^{2} - 4}{x^{2}} \Rightarrow y' = 0\Leftrightarrow \left\lbrack \begin{matrix} x = 2 \in (0; + \infty) \\ x = - 2 otin (0; + \infty) \\ \end{matrix} ight..

    Bảng biến thiên

    Vậy giá trị nhỏ nhất là m = 4 khi x = 2.

    Cách 2:

    Với x \in (0;\ + \infty) \Rightarrow x;\ \frac{4}{x} > 0.

    Áp dụng bất đẳng thức Cô si ta có: x + \frac{4}{x} \geq 2\sqrt{x.\frac{4}{x}} = 4.

    Dấu bằng xảy ra khi và chỉ khi \left\{ \begin{matrix} x > 0 \\ x = \dfrac{4}{x} \\ \end{matrix} ight.\ \Leftrightarrow x = 2. Vậy m = 4 khi x = 2.

  • Câu 8: Thông hiểu

    Mệnh đề nào sau đây là mệnh đề sai?

    Mệnh đề nào sau đây là mệnh đề sai?

    Ta thấy: y = {2^{ - x}} = {\left( {\frac{1}{2}} ight)^x}

    Do vậy đồ thị của hàm số y = {2^{ - x}} không có tiệm cận đứng

  • Câu 9: Nhận biết

    Mệnh đề nào sau đây đúng

    Mệnh đề nào sau đây đúng?

     Trong không gian chỉ có 5 loại khối đa diện đều như hình vẽ sau:

    - Khối lập phương có 6 mặt.

    \Rightarrow "Mọi khối đa diện đều có số mặt là những số chia hết cho 4" \Rightarrow Sai.

    - Khối lập phương và khối bát diện đều có cùng số cạnh là 12. \Rightarrow Đúng

    - Khối tứ diện đều không có tâm đối xứng.

    \Rightarrow "Khối tứ diện đều và khối bát diện đều có 1 tâm đối xứng": Sai.

    - Khối 12 mặt đều có 20 đỉnh. Khối 20 mặt đều có 12 đỉnh.

    \Rightarrow "Khối mười hai mặt đều và khối hai mươi mặt đều có cùng số đỉnh": Sai

     

  • Câu 10: Vận dụng cao

    Tìm m để BPT mũ có nghiệm thỏa mãn

    Cho bất phương trình: {9^x} + \left( {m - 1} ight){.3^x} + m > 0\,\,\left( 1 ight). Tìm tất cả các giá trị của tham số để bất phương trình (1) nghiệm đúng \forall x>1.

    Đặt t=3^x.

    Vì  x > 1 \Rightarrow t > 3. Bất phương trình đã cho thành: {t^2} + \left( {m - 1} ight).t + m > 0 nghiệm đúng \forall t \geqslant 3

    \Leftrightarrow \frac{{{t^2} - t}}{{t + 1}} > - m nghiệm đúng \forall t \geqslant 3.

    Xét hàm số:  g\left( t ight) = t - 2 + \frac{2}{{t + 1}},\forall t > 3,g'\left( t ight) = 1 - \frac{2}{{{{\left( {t + 1} ight)}^2}}} > 0,\forall t > 3.

    Hàm số đồng biến trên \left[ {3; + \infty } ight) và g\left( 3 ight) = \frac{3}{2}. Yêu cầu bài toán tương đương - m \leqslant \frac{3}{2} \Leftrightarrow m \geqslant - \frac{3}{2}.

  • Câu 11: Vận dụng cao

    Chọn đáp án thích hợp

    Tập hợp tất cả các giá trị của tham số m để hàm số y = \frac{\sqrt{x^{2} - 8x} - 4}{\sqrt{x^{2} - 8x} + m} nghịch biến trên ( - 1;0) là:

    Đặt t = \sqrt{x^{2} - 8x}

    Điều kiện xác định x^{2} - 8x \geq 0 \Leftrightarrow \left\lbrack \begin{matrix} x \leq 0 \\ x \geq 8 \\ \end{matrix} ight.

    Xét hàm t = \sqrt{x^{2} - 8x};x \in ( - 1;0) ta có:

    t' = \frac{2x - 8}{2\sqrt{x^{2} - 8x}} = \frac{x - 4}{\sqrt{x^{2} - 8x}} < 0;\forall x \in ( - 1;0)

    Ta có bảng biến thiên

    Từ bảng biến thiên ta thấy hàm số t = \sqrt{x^{2} - 8x} nghịch biến trên khoảng ( - 1;0) và t \in (0;3)

    Khi đó yêu cầu bài toán \Leftrightarrow y = \frac{t - 4}{t + m} đồng biến trên (0;3)

    Điều kiện xác định D\mathbb{= R}\backslash\left\{ - m ight\}

    Ta có: y' = \frac{m + 4}{(t + m)^{2}};\forall x \in D

    Để hàm số đồng biến trên (0;3) thì

    \left\{ \begin{matrix} y' > 0 \\ - m otin (0;3) \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m + 4 > 0 \\ \left\lbrack \begin{matrix} - m \leq 0 \\ - m \geq 3 \\ \end{matrix} ight.\ \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m > - 4 \\ \left\lbrack \begin{matrix} m \geq 0 \\ m \leq - 3 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} - 4 < m \leq - 3 \\ m \geq 0 \\ \end{matrix} ight.

    Vậy đáp án cần tìm là m \in ( - 4; - 3brack \cup \lbrack 0; + \infty)

  • Câu 12: Nhận biết

    Tính giá trị của biểu thức M = a – b

    Biết \frac{{{x^{{a^2}}}}}{{{x^{{b^2}}}}} = {x^{16}} với x > 1 và a + b = 2. Tính giá trị của biểu thức M = a – b.

     Ta có: 

    \begin{matrix} \dfrac{{{x^{{a^2}}}}}{{{x^{{b^2}}}}} = {x^{16}} \hfill \\ \Leftrightarrow {x^{{a^2} - {b^2}}} = {x^{16}} \hfill \\ \Leftrightarrow {a^2} - {b^2} = 16 \hfill \\ \Leftrightarrow \left( {a + b} ight)\left( {a - b} ight) = 16 \hfill \\ \Rightarrow a - b = 8 \hfill \\ \end{matrix}

  • Câu 13: Thông hiểu

    Tính V

    Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp đã cho.

     

    Gọi I là tâm đường tròn ngoại tiếp tam giác ABC. Vì S.ABC là khối chóp đều nên suy ra \,SI \bot \left( {ABC} ight).

    Gọi M là trung điểm của BC\,\, \Rightarrow \,\,AI = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}

    Tam giác SAI vuông tại I, có:

    SI = \sqrt {S{A^2} - S{I^2}} = \sqrt {{{\left( {2a} ight)}^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} ight)}^2}} = \frac{{a\sqrt {33} }}{3}

    Diện tích tam giác ABC là:  {S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}

    Vậy thể tích khối chóp:  {V_{S.ABCD}} = \frac{1}{3}{S_{\Delta ABC}}.SI = \frac{{\sqrt {11} \,{a^3}}}{{12}}

  • Câu 14: Nhận biết

    Xác định hàm số đồng biến trên D

    Tìm hàm số luôn đồng biến trên từng khoảng xác định?

    Xét hàm số y = \frac{- x - 8}{x + 3}

    Tập xác định D\mathbb{= R}\backslash\left\{ - 3 ight\}. Ta có: y' = \frac{5}{\left( x + 3^{2} ight)} > 0;\forall x eq 3

    Vậy hàm số đồng biến trên các khoảng ( - \infty; - 3),( - 3; + \infty).

  • Câu 15: Thông hiểu

    Tính V lăng trụ biết V chóp

    Tính thể tích Vcủa khối lăng trụ ABC.A'B'C' biết thể tích khối chóp A.BCB'C' bằng 2a^3

    Ta có thể tích khối chóp: {V_{A.A'B'C'}} = \frac{1}{3}{V_{ABC.A'B'C'}}

    Suy ra:

    {V_{A.BCB'C'}} = \frac{2}{3}{V_{ABC.A'B'C'}}\xrightarrow{{}}{V_{ABC.A'B'C'}} = \frac{3}{2}{V_{A.BCB'C'}} = \frac{3}{2}.2{a^3} = 3{a^3}.

  • Câu 16: Vận dụng

    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) và đồ thị của hàm số y = f'(x) như hình vẽ sau:

    Hàm số g(x) = f\left( |x| ight) +2021 có bao nhiêu điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) và đồ thị của hàm số y = f'(x) như hình vẽ sau:

    Hàm số g(x) = f\left( |x| ight) +2021 có bao nhiêu điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 17: Vận dụng

    Tìm các số thực dương m theo yêu cầu bài toán

    Cho hàm số y = x^{4} - 3x^{2} - 2. Tìm số thực dương m để đường thẳng y = m cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ.

    Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:

    x^{4} - 3x^{2} - 2 = m \Leftrightarrow x^{4} - 3x^{2} - 2 - m = 0\ \ \ \ \ \ \ \ \ (1).

    Vì m > 0 \Leftrightarrow - 2 - m < 0 hay phương trình (1) luôn có hai nghiệm phân biệt thỏa mãn:

    x^{2} = \frac{3 + \sqrt{4m + 17}}{2} \Rightarrow x_{1} = \sqrt{\frac{3 + \sqrt{4m + 17}}{2}}và x_{2} = - \sqrt{\frac{3 + \sqrt{4m + 17}}{2}}.

    Khi đó: A\left( x_{1};m ight), B\left( x_{2};m ight).

    Ta có tam giác OAB vuông tại O, trong đó O là gốc tọa độ \Leftrightarrow \overrightarrow{OA}.\overrightarrow{OB} = 0 \Leftrightarrow x_{1}.x_{2} + m^{2} = 0.

    \Leftrightarrow \frac{3 + \sqrt{4m + 17}}{2} = m^{2}

    \Leftrightarrow \left\{ \begin{matrix} 2m^{2} - 3 \geq 0 \\ 4m^{4} - 12m^{2} - 4m - 8 = 0 \\ \end{matrix} ight.\ \overset{m > 0}{\leftrightarrow}m = 2.

    Vậy m = 2 là giá trị cần tìm.

  • Câu 18: Nhận biết

    Hàm số nào nghịch biến trên tập số thực?

    Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?

     Ta có:

    y = {\log _{\frac{\pi }{4}}}\left( {2{x^2} + 1} ight);y = {\log _{\frac{1}{2}}}x là các hàm số không xác định trên \mathbb{R}

    Vì \frac{2}{e} < 1 \Rightarrow y = {\left( {\frac{2}{e}} ight)^x} nghịch biến trên \mathbb{R}

  • Câu 19: Vận dụng

    Tính V biết tổng diện tích

    Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=SB, SC=SD và \left( {SAB} ight) \bot \left( {SCD} ight). Tổng diện tích hai tam giác SAB và SCD bằng \frac{{7{a^2}}}{{10}}. Tính thể tích V của khối chóp  S.ABCD?

     

    Gọi M, N lần lượt là trung điểm của AB và CD.

    Tam giác SAB cân tại S suy ra SM \bot AB \Rightarrow SM \bot d với d = \left( {SAB} ight) \cap \left( {SCD} ight).

    Vì \left( {SAB} ight) \bot \left( {SCD} ight) suy ra SM \bot \left( {SCD} ight) \Rightarrow SM \bot SN và \left( {SMN} ight) \bot \left( {ABCD} ight)

    Kẻ SH \bot MN\xrightarrow{{}}SH \bot \left( {ABCD} ight).

    Ta có {S_{\Delta SAB}} + {S_{\Delta SCD}} = \frac{{7{a^2}}}{{10}}

    \Leftrightarrow \frac{1}{2}AB.SM + \frac{1}{2}CD.SN = \frac{{7{a^2}}}{{10}}\xrightarrow{{}}SM + SN = \frac{{7a}}{5}.

    Tam giác SMN vuông tại S nên S{M^2} + S{N^2} = M{N^2} = {a^2}

    Giải hệ:

    \left\{ \begin{gathered} SM + SN = \frac{{7a}}{5} \hfill \\ S{M^2} + S{N^2} = {a^2} \hfill \\ \end{gathered} ight.  \Leftrightarrow SM = \frac{{3a}}{5}{\text{ }} hoặc  SN = \frac{{4a}}{5}

    \xrightarrow{{}}SH = \frac{{SM.SN}}{{MN}} = \frac{{12a}}{{25}}

    Vậy thể tích khối chóp V_{S.ABCD} = \frac{1}{3}.{S_{ABCD}}.SH = \frac{{4{a^3}}}{{25}}.

  • Câu 20: Thông hiểu

    Ghi đáp án vào ô trống

    Cho phương trình log_{\frac{1}{2}}(2x - m) + log_{2}(3 - x) = 0, m là tham số. Hỏi có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm?

    Đáp án: 5

    Đáp án là:

    Cho phương trình log_{\frac{1}{2}}(2x - m) + log_{2}(3 - x) = 0, m là tham số. Hỏi có bao nhiêu giá trị nguyên dương của m để phương trình có nghiệm?

    Đáp án: 5

    ĐKXĐ: \left\{ \begin{matrix} 2x - m > 0 \\ 3 - x > 0 \\ \end{matrix} \Leftrightarrow \left\{ \begin{matrix} 2x - m > 0 \\ x < 3 \\ \end{matrix} ight.\ ight.\ .

    Ta có:

    log_{\frac{1}{2}}(2x - m) + log_{2}(3 -x) = 0

    \Leftrightarrow - log_{2}(2x - m) + log_{2}(3 - x) = 0

    \Leftrightarrow log_{2}(2x - m) = log_{2}(3 - x)

    \Leftrightarrow 2x - m = 3 - x \Leftrightarrow 3x = m + 3

    Để phương trình có nghiệm thì m + 3 < 9 \Leftrightarrow m < 6.

    Kết hợp điều kiện m là số nguyên dương ta có m ∈ {1;2;3;4;5}.

    Vậy có 5 giá trị của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 21: Vận dụng

    Tìm số cực trị của hàm số lũy thừa

    Hàm số y = \sqrt[3]{{{{\left( {{x^2} - 2x - 3} ight)}^2}}} + 2 có bao nhiêu điểm cực trị?

    Tập xác định D = \mathbb{R}

    Ta có: y' = \frac{2}{3}.\frac{{2x - 2}}{{\sqrt[3]{{{x^2} - 2x - 3}}}};\left( {x e - 1;x e 3} ight)

    Ta có bảng biến thiên như sau:

    Tìm số cực trị của hàm số lũy thừa

    Vậy hàm số đã cho có ba điểm cực trị

  • Câu 22: Vận dụng

    Ghi đáp án vào ô trống

    Cho hàm số y = \frac{mx^{2} + \left( m^{2} + m + 2 ight)x + m^{2} + 3}{x + 1}. Tìm m \in \mathbb{R} để khoảng cách từ gốc O đến tiệm cận xiên hoặc ngang là nhỏ nhất.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = \frac{mx^{2} + \left( m^{2} + m + 2 ight)x + m^{2} + 3}{x + 1}. Tìm m \in \mathbb{R} để khoảng cách từ gốc O đến tiệm cận xiên hoặc ngang là nhỏ nhất.

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 23: Nhận biết

    V lăng trụ đứng

    Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và AC = a\sqrt 2. Tính thể tích của khối lăng trụ đã cho.

     

    Tam giác ABC vuông cân tại B,

    suy ra BA = BC = \frac{{AC}}{{\sqrt 2 }} = a \Rightarrow {S_{\Delta ABC}} = \frac{{{a^2}}}{2}

    Vậy thể tích khối lăng trụ V = {S_{\Delta ABC}}.BB' = \frac{{{a^3}}}{2}

  • Câu 24: Thông hiểu

    Xác định tập hợp tham số m thỏa mãn yêu cầu

    Tập hợp tất cả các giá trị của tham số m để hàm số y = x^{4} - 5(m - 3)x^{2} + 3m^{2} - 4 đạt cực tiểu tại x = 0 là:

    Ta có: y' = 4x^{3} - 10(m - 3)x

    \Rightarrow y' = 0 \Leftrightarrow\left\lbrack \begin{matrix}x = 0 \\x^{2} = \dfrac{10(m - 3)}{4} \\\end{matrix} ight.

    Trường hợp 1: m - 3 > 0 \Leftrightarrow m > 3. Khi đó ta có bảng xét dấu như sau:

    Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực đại nên trường hợp này không thỏa mãn.

    Trường hợp 2: m - 3 \leq 0 \Leftrightarrow m \leq 3 ta có bảng xét dấu như sau:

    Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực tiểu. Vậy m \leq 3 thỏa mãn yêu cầu bài toán.

  • Câu 25: Nhận biết

    Tìm tập nghiệm của BPT logarit

    Bất phương trình \log _{0,2}^2x - 5{\log _{0,2}}x < - 6 có tập nghiệm là:

    Điều kiện: x>0

    Ta có:

    \log _{0,2}^2 - 5{\log _{0,2}}x < - 6 \Leftrightarrow 2 < {\log _{0,2}}x < 3 \Leftrightarrow \frac{1}{{125}} < x < \frac{1}{{25}}

    Vậy BPT đã cho có tập nghiệm là S = \left( {\frac{1}{{125}};\frac{1}{{25}}} ight).

  • Câu 26: Vận dụng

    Tính

    Gọi x_1, x_2 là 2 nghiệm của phương trình {\log _3}\left( {{x^2} - x - 5} ight) = {\log _3}\left( {2x + 5} ight).

    Khi đó \left| {{x_1} - {x_2}} ight| bằng:

     Ta có: {\log _3}\left( {{x^2} - x - 5} ight) = {\log _3}\left( {2x + 5} ight) \Leftrightarrow \left\{ \begin{gathered} 2{\text{x}} + 5 > 0 \hfill \\ {x^2} - x - 5 = 2x + 5 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > - \frac{5}{2} \hfill \\ \left[ \begin{gathered} x = 5 \hfill \\ x = - 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} x = 5 \hfill \\ x = - 2 \hfill \\ \end{gathered} ight.

    Suy ra \left| {{x_1} - {x_2}} ight| =|5-(-2)|=|5+2|=7. 

  • Câu 27: Nhận biết

    Điều kiện xác định

    Điều kiện xác định của phương trình {\log _5}(x - 1) = {\log _5}\frac{x}{{x + 1}} là: 

     Biểu thức {\log _5}(x - 1) = {\log _5}\frac{x}{{x + 1}} và xác định 

    \Leftrightarrow \left\{ \begin{gathered} \frac{x}{{x + 1}} > 0 \hfill \\ x - 1 > 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x < - 1 \vee x > 0 \hfill \\ x > 1 \hfill \\ \end{gathered} ight. \Leftrightarrow x > 1

  • Câu 28: Vận dụng

    Khẳng định nào sau đây đúng?

    Cho biết {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}, khẳng định nào sau đây đúng?

    Điều kiện: x - 2 > 0 \to x > 2

    Ta có:

    - \frac{1}{3} > - \frac{1}{6} \Rightarrow {\left( {x - 2} ight)^{ - \frac{1}{3}}} > {\left( {x - 2} ight)^{ - \frac{1}{6}}}

    \Rightarrow x - 2 < 1 \Rightarrow x < 3

    Vậy 2 < x < 3

  • Câu 29: Vận dụng

    Chọn câu đúng

    Mỗi khối đa diện đều mà mỗi đỉnh của nó đều là đỉnh chung của ba mặt thì số đỉnh Đ và số cạnh C của các khối đa diện đó luôn thỏa mãn?

    Do mỗi đỉnh là đỉnh chung của đúng ba mặt nên suy ra số cạnh của khối đa diện là 3Đ.

    Mặt khác, mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức 3Đ =2C.

  • Câu 30: Vận dụng

    Giải BPT

    Tập nghiệm của bất phương trình {\log _{\frac{1}{2}}}\left( {{{\log }_2}\left( {2x - 1} ight)} ight) > 0 là:

     Điều kiện: \left\{ \begin{gathered} 2x - 1 > 0 \hfill \\ {\log _2}(2x - 1) > 0 \hfill \\ \end{gathered} ight. \Leftrightarrow x > 1.

    Ta có: {\log _{\frac{1}{2}}}\left( {{{\log }_2}\left( {2x - 1} ight)} ight) > 0 \Leftrightarrow {\log _{\frac{1}{2}}}\left( {{{\log }_2}\left( {2x - 1} ight)} ight) > {\log _{\frac{1}{2}}}1

    \Leftrightarrow \left\{ \begin{gathered} {\log _2}(2x - 1) < 1 \hfill \\ {\log _2}(2x - 1) > 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} 0 < 2x - 1 < 2 \hfill \\ 2x - 1 > 1 \hfill \\ \end{gathered} ight. \Leftrightarrow 1 < x < \frac{3}{2} (thỏa mãn điều kiện)

    Vậy tập nghiệm của bất phương trình đã cho là  S = \left( {1;\frac{3}{2}} ight).

  • Câu 31: Vận dụng

    Ghi đáp án vào ô trống

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Bác H cần xây dựng một bể nước mưa có thể tích V = 8\left( m^{3} ight) dạng hình hộp chữ nhật với chiều dài gấp \frac{4}{3} lần chiều rộng, đáy và nắp đổ bê tông, cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980000 đồng trên một mét vuông và ở nắp để hở một khoảng hình vuông có diện tích bằng \frac{2}{9} diện tích nắp bể. Tính chi phí thấp nhất mà bác H phải chi trả (làm tròn đến hàng triệu đồng).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 32: Vận dụng

    Chọn phương án thích hợp

    Viết phương trình mặt cầu (S) qua ba điểm A(2,0,1);\ \ \ B(1,3,2);\ \ \ C(3,2,0) có tâm nằm trong mặt phẳng (xOy)

    Ta có:

    (S):x^{2} + y^{2} + z^{2} - 2ax - 2by + d = 0 vì tâm I \in (xOy) \Rightarrow c = 0

    A,\ B,\ C \in (S)\Rightarrow \left\{ \begin{matrix} 4a - d = 5 \\ 2a + 6b - d = 14 \\ 6a + 4b - d = 13 \\ \end{matrix} \right.\Rightarrow \left\{ \begin{matrix} 2a - 6b = - 9 \\ 2a + 4b = 8 \\ \end{matrix} \right.

    \Rightarrow a = \frac{3}{5};\ \ b = \frac{17}{10};\ \ c = 0;\ \ d = - \frac{13}{5}

    \Rightarrow (S):x^{2} + y^{2} + z^{2} - \frac{6x}{5} - \frac{17y}{5} - \frac{13}{5} = 0

  • Câu 33: Thông hiểu

    Mênh đề đúng?

    Gọi Đ là số các đỉnh, M là số các mặt, C là số các cạnh của một hình đa diện bất kỳ. Mệnh đề nào sau đây là đúng?

    Xét hình đa diện là một hình bất kì, ví dụ lấy đa diện là hình tứ diện thì ta có số đỉnh, mặt và cạnh lần lượt là:

    Đ=4; M=4; C=6

  • Câu 34: Nhận biết

    Tập xác định của hàm số f(x)

    Tập xác định của hàm số f\left( x ight) = {\left( {{x^2} - 1} ight)^{ - 2}} là:

    Hàm số f\left( x ight) = {\left( {{x^2} - 1} ight)^{ - 2}} xác định khi {x^2} - 1 e 0 \Rightarrow x e \pm 1

    Vậy tập xác định của hàm số là D = \mathbb{R}\backslash \left\{ { \pm 1} ight\}

  • Câu 35: Nhận biết

    Xác định tiệm cận ngang của đồ thị hàm số

    Tiệm cận ngang của đồ thị hàm số y = \frac{2020}{x - 1} là đường thẳng có phương trình?

    Ta có: \lim_{x ightarrow \pm \infty}y = \lim_{x ightarrow \pm \infty}\frac{2020}{x - 1} = 0 nên tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình y = 0.

  • Câu 36: Thông hiểu

    Tính giá trị của biểu thức P

    Cho {\log _a}b = 2;{\log _a}c = 3. Tính giá trị của biểu thức P = {\log _a}\left( {a{b^3}{c^3}} ight)

    Ta có:

    \begin{matrix} P = {\log _a}\left( {a{b^3}{c^3}} ight) \hfill \\ = {\log _a}a + {\log _a}{b^3} + {\log _a}{c^3} \hfill \\ = 1 + 3{\log _a}b + 5{\log _a}c \hfill \\ = 1 + 3.2 + 5.3 = 22 \hfill \\ \end{matrix}

  • Câu 37: Nhận biết

    Xác định tọa độ điểm thuộc mặt cầu

    Mặt cầu (S):\ x^{2} + y^{2} + z^{2} - 2x + 10y + 3z + 1 = 0 đi qua điểm có tọa độ nào sau đây?

    Lần lượt thay tọa độ các điểm vào phương trình mặt cầu. Tọa độ điểm nào thỏa mãn phương trình thì điểm đó thuộc mặt cầu.

    Kiểm tra đáp án thu được kết quả là: điểm (4; - 1;0). thuộc mặt cầu đã cho.

  • Câu 38: Nhận biết

    Giá trị của biểu thức

    Giá trị của biểu thức A = {\log _{{2^{2018}}}}4 - \frac{1}{{1009}} + \ln {e^{2018}}

    Ta có:

    A = {\log _{{2^{2018}}}}4 - \frac{1}{{1009}} + \ln {e^{2018}} = {\log _{{2^{2018}}}}{2^2} - \frac{1}{{1009}} + 2018.\ln e

    = \frac{1}{{1009}} - \frac{1}{{1009}} + 2018 = 2018

  • Câu 39: Nhận biết

    Diện tích xung quanh

    Cho hình nón đỉnh S có bán kính đáy R = a\sqrt 2, góc ở đỉnh bằng {60^0}. Diện tích xung quanh của hình nón bằng:

    Diện tích xung quanh

     Theo giả thiết, ta có OA = a\sqrt 2 và \widehat {OSA} = {30^0}.

    Suy ra độ dài đường sinh:  \ell = SA = \frac{{OA}}{{\sin {{30}^0}}} = 2a\sqrt 2

    Vậy diện tích xung quanh bằng: {S_{xq}} = \pi R\ell = 4\pi {a^2} (đvdt). 

  • Câu 40: Nhận biết

    Tìm hàm số tương ứng với đồ thị

    Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ cho sau đây?

    Đồ thị hàm số bậc 4 có hệ số a < 0 và có ba điểm cực trị nên ab < 0 nên chọn y = - x^{4} + 2x^{2} + 1.

  • Câu 41: Thông hiểu

    Tính bán kính đáy

    Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:

     Gọi bán kính đáy là R.

    Từ giả thiết suy ra h= 2a và chu vi đáy bằng a .

    Do đó 2\pi R = a \Leftrightarrow R = \frac{a}{{2\pi }}.

  • Câu 42: Thông hiểu

    Chọn phương án thích hợp

    Dân số thế giới được tính theo công thức S = A. e \ ^{nr} trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hằng năm. Cho biết năm 2005 Việt Nam có khoảng 80902400 người và tỉ lệ tăng dân số là 1,47\% một năm. Như vậy, nếu tỉ lệ tăng dân số hàng năm không đổi thì tối thiểu đến năm bao nhiêu dân của Việt Nam có khoảng 93713000 người?

    Ta có:

    S = A \cdot e^{nr} \Leftrightarrow e^{nr} = \frac{S}{A} \Leftrightarrow nr = \ln\frac{S}{A} \Leftrightarrow n = \frac{1}{r}\ln\frac{S}{A}

    Với S = 93713700 người; A = 80902400 người; r = \frac{1,47}{100} = 0,0147/năm.

    Suy ra n = \frac{1}{0,0147}\ln\frac{93713000}{80902400} \approx 10.

    Vậy tối thiểu đến năm 2015 thì dân số của Việt Nam có khoảng 93713000 người.

  • Câu 43: Thông hiểu

    Khẳng định nào sau đây sai?

    Cho hàm số y = {x^{\frac{{ - 3}}{4}}}. Khẳng định nào sau đây sai?

    Hàm số y = {x^{\frac{{ - 3}}{4}}} có các tính chất như sau:

    Đồ thị hàm số nhận trục tung làm tiệm cận đứng

    Đồ thị hàm số nhận trục hoành làm tiệm cận ngang

    Là hàm số nghịch biến trên \left( {0; + \infty } ight)

  • Câu 44: Thông hiểu

    Chọn đáp án đúng

    Số dân số của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức f(t) = \frac{26t + 10}{t + 5} (f(t) được tính bằng nghìn người). Biết rằng đạo hàm của hàm số f(t) biểu thị tốc độ gia tăng dân số của thị trấn ( đơn vị là nghìn người/ năm). Vào năm nào thì tốc độ gia tăng dân số là \frac{2}{15} nghìn người/ năm?

    Ta có f'(t) = \frac{{120}}{{{{\left( {t + 5} ight)}^2}}},t \geqslant 0

    Lại có

    f'(t) = \frac{2}{{15}} \Leftrightarrow \frac{{120}}{{{{\left( {t + 5} ight)}^2}}} = \frac{2}{{15}}

    \Leftrightarrow (t + 5)^{2} = 900 \Leftrightarrow t = 25\ do\ t \geq 0)

    Vậy dự báo vào năm 1995 thì tốc độ gia tăng dân số là \frac{2}{15} nghìn người/ năm.

  • Câu 45: Thông hiểu

    Viết biểu thức P dưới dạng lũy thừa với số mũ hữu tỉ

    Viết biểu thức P = \frac{{{a^2}.{a^{\frac{5}{2}}}.\sqrt[3]{{{a^4}}}}}{{\sqrt[6]{{{a^5}}}}};\left( {a > 0} ight) dưới dạng lũy thừa với số mũ hữu tỉ

    Ta có: P = \dfrac{{{a^2}.{a^{\frac{5}{2}}}.\sqrt[3]{{{a^4}}}}}{{\sqrt[6]{{{a^5}}}}} = \dfrac{{{a^2}.{a^{\frac{5}{2}}}.{a^{\frac{4}{3}}}}}{{{a^{\frac{5}{6}}}}} = {a^5}

  • Câu 46: Vận dụng

    Tính giá trị của biểu thức M

    Cho hàm số f\left( x ight) = \ln \frac{{x + 1}}{{x + 4}}. Tính giá trị của biểu thức M = f'\left( 0 ight) + f'\left( 3 ight) + f'\left( 6 ight) + ... + f'\left( {2019} ight)

    Với x \in \left[ {0; + \infty } ight) ta có: \left\{ {\begin{array}{*{20}{c}} {x + 1 > 0} \\ {x + 4 > 0} \end{array}} ight. \Rightarrow f\left( x ight) = \ln \frac{{x + 1}}{{x + 4}} = \ln \left( {x + 1} ight) - \ln \left( {x + 4} ight)

    Ta có: f'\left( x ight) = \frac{1}{{x + 1}} - \frac{1}{{x + 4}} do đó:

    \begin{matrix} M = f'\left( 0 ight) + f'\left( 3 ight) + f'\left( 6 ight) + ... + f'\left( {2019} ight) \hfill \\ M = \left( {1 - \dfrac{1}{4}} ight) + \left( {\dfrac{1}{4} - \dfrac{1}{7}} ight) + \left( {\dfrac{1}{7} - \dfrac{1}{{10}}} ight) + ... + \left( {\dfrac{1}{{2020}} - \dfrac{1}{{2023}}} ight) \hfill \\ M = 1 - \dfrac{1}{{2023}} = \dfrac{{2022}}{{2023}} \hfill \\ \end{matrix}

  • Câu 47: Vận dụng cao

    Tìm số giá trị nguyên của tham số m

    Cho hàm số f(x) liên tục trên \mathbb{R} và có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình f^{2}\left( \cos x \right) + (m - 2022)f\left( \cos x \right) + m - 2023 = 0 có đúng 6 nghiệm phân biệt thuộc đoạn \lbrack 0;2\pi\rbrack là

    Ta có f^{2}\left( \cos x ight) + (m - 2022)f\left( \cos x ight) + m - 2023 = 0

    \Leftrightarrow \left\lbrack \begin{matrix} f\left( \cos x ight) = - 1 \\ f\left( \cos x ight) = 2023 - m \\ \end{matrix} ight. (1)

    * Với f\left( \cos x ight) = - 1

    Dựa vào đồ thị ta có f\left( \cos x ight) = - 1

    \Leftrightarrow \left\lbrack \begin{matrix} \cos x = 0 \\ \cos x = x_{1};\left( x_{1} > 1 ight)(VN) \\ \end{matrix} ight.

    \Leftrightarrow x = \frac{\pi}{2} + k\pi

    Vì x \in \lbrack 0;2\pibrack \Rightarrow x \in \left\{ \frac{\pi}{2};\frac{3\pi}{2} ight\}

    * Với f\left( \cos x ight) = 2023 - m

    Đặt t = \cos x\ \ \left( t \in \lbrack - 1;1brack ight)

    Với t \in ( - 1;1brack thì phương trình t = \cos x có hai nghiệm phân biệt thuộc \lbrack 0;2\pibrack.

    Với t = - 1 thì phương trình t = \cos x có một nghiệm thuộc \lbrack 0;2\pibrack

    Phương trình trở thành f(t) = 2023 - m

    Để phương trình (1) có tất cả 6 nghiệm phân biệt thì phương trình f\left( \cos x ight) = 2023 - m có 4 nghiệm phân biệt, hay phương trình f(t) = 2023 - m có hai nghiệm t \in ( - 1;1brack

    Dựa vào đồ thị ta có để phương trình f(t) = 2023 - m có hai nghiệm t \in ( - 1;1brack thì - 1 < 2023 - m \leq 1 \Leftrightarrow 2022 \leq m < 2024

    Vì m nguyên nên m \in \left\{ 2022;2023 ight\}

    Vậy có 2 giá trị nguyên của m thỏa mãn.

  • Câu 48: Vận dụng cao

    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) = (m - 1)x^{3} -5x^{2} + (3 + m)x + 3 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f\left( |x| ight) có đúng ba cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = (m - 1)x^{3} -5x^{2} + (3 + m)x + 3 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = f\left( |x| ight) có đúng ba cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 49: Thông hiểu

    Tính giá trị của biểu thức

    Biết bất phương trình \log_{2}\left( 3^{x}- 3 ight)\log_{8}\left( 3^{x}2^{- 2} - \frac{3}{4} ight) \leq1 có tập nghiệm là đoạn [a; b]. Giá trị biểu thức a + b bằng:

    Điều kiện \left\{ \begin{matrix} 3^{x} - 3 > 0 \\ 3^{x - 2} - \frac{3}{4} > 0 \\ \end{matrix} \Leftrightarrow x > 1 ight..

    log_{2}\left( 3^{x} - 3ight)log_{8}\left( 3^{x}2^{- 2} - \frac{3}{4} ight) \leq1

    \Leftrightarrow log_{2}\left( 3^{x} - 3 ight).\frac{1}{3}\left\lbrack log_{2}\left( 3^{x} - 3 ight) - 2 ightbrack - 1 \leq 0

    Đặt t = log_{2}\left( 3^{x} - 3 ight)

    Ta có:

    \frac{1}{3}t(t - 2) - 1 \leq 0 \Leftrightarrow \frac{1}{3}t^{2} - \frac{2}{3}t - 1 \leq 0

    \Leftrightarrow - 1 \leq t \leq 3 \Leftrightarrow - 1 \leq log_{2}\left( 3^{x} - 3 ight) \leq 3

    \Leftrightarrow \frac{7}{2} \leq 3^{x} \leq 11 \Leftrightarrow log_{3}\frac{7}{2} \leq x \leq log_{3}11

    Suy ra tập nghiệm là S = \left\lbrack log_{3}\frac{7}{2};log_{3}11 ightbrack \Rightarrow a + b = log_{3}\frac{77}{2}.

  • Câu 50: Thông hiểu

    Chọn khẳng định đúng

    Chọn khẳng định đúng trong các khẳng định sau:

    Tâm tất cả các mặt của một hình tứ diện đều là các đỉnh của một hình tứ diện đều:

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 12 Đề 1 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại
1
21 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 1 Toán 12 Đề 1
Thời gian còn lại 90:00 Số câu đã làm 0/50
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này
🖼️

Toán 12 (cũ)
Xem thêm