Diện tích toàn phần
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh có cạnh bằng 2R. Diện tích toàn phần của khối trụ bằng:
Do thiết diện đi qua trục hình trụ nên ta có .
Diện tích toàn phần là: (đvdt).
Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 2: Mặt trụ - Mặt nón - Mặt cầu Toán 12 các em nhé!
Diện tích toàn phần
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh có cạnh bằng 2R. Diện tích toàn phần của khối trụ bằng:
Do thiết diện đi qua trục hình trụ nên ta có .
Diện tích toàn phần là: (đvdt).
Chọn đáp án thích hợp
Phương trình mặt câu tâm ![]() có bán kính
có bán kính ![]() là:
là:
Đáp án cần tìm là:
.
Diện tích toàn phần
Trong không gian, cho hình chữ nhật ABCD có ![]() và
và ![]() . Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:
. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN , ta được một hình trụ. Diện tích toàn phần của hình trụ bằng:

Theo giả thiết ta được hình trụ có chiều cao , bán kính đáy
Do đó diện tích toàn phần:
Chọn đáp án thích hợp
Cho 4 điểm ![]() và
và ![]() . Mặt cầu tâm A và tiếp xúc với mặt phẳng
. Mặt cầu tâm A và tiếp xúc với mặt phẳng ![]() có phương trình là:
có phương trình là:
Mặt phẳng đi qua
và có vectơ pháp tuyến
Vì mặt cầu có tâm A tiếp xúc với mặt phẳng
nên bán kính
.
Vậy phương trình mặt cầu
Chọn phương án thích hợp
Trong không gian ![]() , cho đường thẳng
, cho đường thẳng  , điểm
, điểm ![]() và mặt cầu
và mặt cầu ![]() :
: ![]() . Gọi
. Gọi ![]() là đường thẳng đi qua M và cắt
là đường thẳng đi qua M và cắt ![]() tại A, cắt
tại A, cắt ![]() tại B sao cho
tại B sao cho ![]() và điểm B có hoành độ là số nguyên. Mặt phẳng trung trực của đoạn AB có phương trình là
và điểm B có hoành độ là số nguyên. Mặt phẳng trung trực của đoạn AB có phương trình là
Từ giả thiết: có tâm
và bán kính
.
.
Vì .
+) Nếu
.
Do
+) Nếu .
Do
.
Do có hoành độ là số nguyên nên
.
Trung điểm là
nên phương trình mặt phẳng trung trực AB:
.
Tính tỉ số thể tích
Từ một tấm tôn hình chữ nhật kích thước ![]() , người ta làm các thùng đựng nước hình trụ có chiều cao bằng
, người ta làm các thùng đựng nước hình trụ có chiều cao bằng ![]() , theo hai cách sau (xem hình minh họa sau đây):
, theo hai cách sau (xem hình minh họa sau đây):
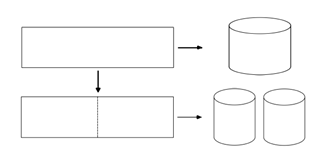
● Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
● Cách 2. Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu ![]() là thể tích của thùng gò được theo cách 1 và
là thể tích của thùng gò được theo cách 1 và ![]() là thể tích của thùng gò được theo cách 2. Khi đó tỉ số
là thể tích của thùng gò được theo cách 2. Khi đó tỉ số ![]() bằng:
bằng:
2 || Hai || hai
Từ một tấm tôn hình chữ nhật kích thước ![]() , người ta làm các thùng đựng nước hình trụ có chiều cao bằng
, người ta làm các thùng đựng nước hình trụ có chiều cao bằng ![]() , theo hai cách sau (xem hình minh họa sau đây):
, theo hai cách sau (xem hình minh họa sau đây):

● Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
● Cách 2. Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng.
Kí hiệu ![]() là thể tích của thùng gò được theo cách 1 và
là thể tích của thùng gò được theo cách 1 và ![]() là thể tích của thùng gò được theo cách 2. Khi đó tỉ số
là thể tích của thùng gò được theo cách 2. Khi đó tỉ số ![]() bằng:
bằng:
2 || Hai || hai
Công thức thể tích khối trụ .
● Ở cách 1, suy ra và
. Do đó
(đvtt).
● Ở cách 2, suy ra mỗi thùng có và
Do đó (đvtt).
Suy ra
Tính bán kính đáy
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chiều dài đường sinh bằng 2a thì bán kính đáy bằng:
Gọi bán kính đáy là R.
Từ giả thiết suy ra và chu vi đáy bằng a .
Do đó .
Chọn phương án đúng
Tìm tập hợp các tâm I của mặt cầu
![]()
![]() ;
; ![]()
Ta có:
Tâm
đường thẳng:
là mặt cầu
Vậy tập hợp các tâm O là phần đường thẳng tương ứng với
Tính diện tích đường tròn
Trong không gian với hệ tọa độ ![]() , mặt phẳng
, mặt phẳng ![]() cắt mặt cầu
cắt mặt cầu ![]() theo giao tuyến là đường tròn có diện tích là:
theo giao tuyến là đường tròn có diện tích là:
Mặt cầu có tâm
và bán kính
Khoảng cách từ đến (P):
Bán kính đường tròn giao tuyến
Diện tích đường tròn giao tuyến .
Tính khoảng cách
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:

Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Tính tang của góc
Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:

Nửa góc ở đỉnh của hình nón là góc .
Hình vuông ABCD cạnh a nên suy ra:
Trong tam giác vuông SOA, ta có .
Tỉ số bán kính
Cho một chiếc cốc có dạng hình nón cụt và một viên bi có đường kính bằng chiều cao của cốc. Đổ đầy nước rồi thả viên bi vào, ta thấy lượng nước tràn ra bằng một phần ba lượng nước đổ vào cốc lúc ban đầu. Biết viên bi tiếp xúc với đáy cốc và thành cốc. Tìm tỉ số bán kính của miệng cốc và đáy cốc (bỏ qua độ dày của cốc).
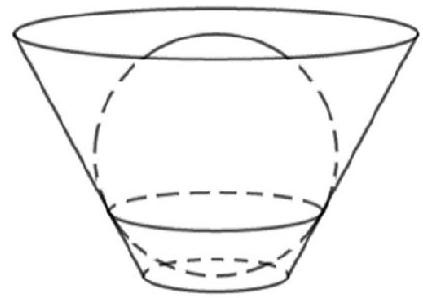
Gọi bán kính viên bi là r; bán kính đáy cốc, miệng cốc lần lượt là . Theo giả thiết thì chiều cao của cốc là
.
Thể tích viên bi là
Thể tích cốc là .
Theo giả thiết thì (1).
Mặt cắt chứa trục của cốc là hình thang cân . Đường tròn tâm
là đường tròn lớn của viên bi, đồng thời là đường tròn nội tiếp hình thang
, tiếp xúc với
lần lượt tại
và tiếp xúc với BB' tại M.

Dễ thấy tam giác BOB' vuông tại O.
Ta có .
Thay (2) vào (1) ta được .
Giải phương trình với điều kiện ta được
.
Tìm phương trình mặt cầu
Cho hai điểm ![]() và
và ![]() . Phương trình mặt cầu đường kính AB là:
. Phương trình mặt cầu đường kính AB là:
Ta có . Mặt cầu đường kính AB có tâm I là trung điểm AB nên
, bán kính
.
Vậy đáp án cần tìm là: .
Tính giá trị của biểu thức
Trong không gian ![]() , cho điểm A(1;2;-1) và mặt phẳng
, cho điểm A(1;2;-1) và mặt phẳng ![]() . Xét các mặt cầu (S) có tâm
. Xét các mặt cầu (S) có tâm ![]() , đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức
, đi qua điểm A, tiếp xúc với mặt phẳng (P) . Tính giá trị của biểu thức ![]() khi (S) có bán kính nhỏ nhất.
khi (S) có bán kính nhỏ nhất.
Gọi H là hình chiếu của I trên mặt phẳng (P) ta có nên R nhỏ nhất khi
thẳng hàng và I là trung điểm của AH.
Phương trình AH đi qua A và vuông góc với mặt phẳng (P) có phương trình là
Tọa độ H là nghiệm của hệ:
Suy ra, ta có:
Tính độ dài cạnh
Một hình trụ có bán kính đáy ![]() , chiều cao hình trụ
, chiều cao hình trụ ![]() . Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?
. Một hình vuông có các đỉnh nằm trên hai đường tròn đáy sao cho có ít nhất một cạnh không song song và không vuông góc với trục hình trụ. Khi đó cạnh của hình vuông bằng bao nhiêu?

Xét hình vuông ABCD có AD không song song và không vuông góc với trục OO’ của hình trụ.
Dựng đường sinh AA', ta có .
Suy ra A’C là đường kính đáy nên
Xét tam giác vuông AA’C, ta có
Suy ra cạnh hình vuông bằng 100 cm.
Tính chu vi đường tròn
Đường tròn giao tuyến của ![]() khi cắt bởi mặt phẳng (Oxy) có chu vi bằng :
khi cắt bởi mặt phẳng (Oxy) có chu vi bằng :
Mặt cầu tâm
, bán kính
.
Ta có : .
Gọi là bán kính đường tròn (C) giao tuyến của mặt cầu
và mặt phẳng (Oxy), ta suy ra :
.
Vậy chu vi (C) bằng: .
Xác định đường kính mặt cầu
Đường kính của mặt cầu ![]() bằng:
bằng:
Mặt cầu có bán kính
suy ra đường kính có độ dài:
Đường kính của mặt cầu bằng: 4.
Tìm tọa độ điểm B
Cho mặt phẳng ![]() và điểm
và điểm ![]() . Gọi
. Gọi ![]() là điểm thuộc tia
là điểm thuộc tia ![]() sao cho mặt cầu tâm
sao cho mặt cầu tâm ![]() , tiếp xúc với mặt phẳng
, tiếp xúc với mặt phẳng ![]() có bán kính bằng 2. Tọa độ điểm
có bán kính bằng 2. Tọa độ điểm ![]() là:
là:
Vì thuộc tia
nên
(với
)
Bán kính của mặt cầu tâm , tiếp xúc với
là
.
Theo giả thiết
Do
Vậy .
Diện tích thiết diện
Cho hình trụ có bán kính đáy bằng R và chiều cao bằng ![]() . Mặt phẳng
. Mặt phẳng ![]() song song với trục của hình trụ và cách trục một khoảng bằng
song song với trục của hình trụ và cách trục một khoảng bằng ![]() . Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng ![]() là:
là:

Giả sử thiết diện là hình chữ nhật ABCD như hình vẽ.
Gọi H là trung điểm BC suy ra suy ra
Khi đó
Suy ra .
Xác định phương trình mặt cầu
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có ![]() trùng với ba trục
trùng với ba trục ![]() . Viết phương trình mặt cầu
. Viết phương trình mặt cầu ![]() tiếp xúc với tất cả các cạnh của hình lập phương.
tiếp xúc với tất cả các cạnh của hình lập phương.
tiếp xúc với 12 cạnh của hình lập phương tại trung điểm của mỗi cạnh. Tâm
là trung điểm của 6 đoạn nối trung điểm của các cặp cạnh đối diện đôi một có độ dài bằng
Bán kính
Độ dài đường sinh
Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho ![]() . Độ dài đường sinh
. Độ dài đường sinh ![]() của hình nón bằng:
của hình nón bằng:

Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.
Tam giác SAS’ vuông tại A và có đường cao AH nên
Thể tích của khối trụ
Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn ![]() , khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:
, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

Gọi (O) và (O') lần lượt là hai đường tròn đáy; .
Dựng AD, CB lần lượt song song với OO' . Dễ dàng có ABCD là hình chữ nhật.
Do .
Gọi H là trung điểm của DC.
.
Ta có .
Suy ra .
Vậy thể tích của khối trụ là .
Tính thể tích khối trụ
Một tấm nhôm hình chữ nhật có hai kích thước là a và 2a (a là độ dài có sẵn). Người ta cuốn tấm nhôm đó thành một hình trụ. Nếu hình trụ được tạo thành có chu vi đáy bằng 2a thì thể tích của nó bằng:
Gọi bán kính đáy là R.
Hình trụ có chu vi đáy bằng 2a nên ta có .
Suy ra hình trụ này có đường cao .
Vậy thể tích khối trụ (đvtt).
Độ dài đường chéo
Bán kính đáy hình trụ bằng 4 cm, chiều cao bằng 6cm. Độ dài đường chéo của thiết diện qua trục bằng:
Thiết diện qua trục của một hình trụ là một hình chữ nhật có hai cạnh lần lượt bằng đường kính đáy và chiều cao của hình trụ.
Vậy hai cạnh của hình chữ nhật là 8 cm và 6 cm.
Do đó độ đài đường chéo:
Tính thể tích khối trụ
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính bằng chiều cao và bằng a. Trên đường tròn tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B sao cho AB = 2a. Thể tích của khối tứ diện OO’AB bằng:

Kẻ đường sinh AA’, gọi D là điểm đối xứng với A’ qua tâm O’ và H là hình chiếu của B trên A’D.
Ta có nên
.
Trong tam giác vuông A'AB có .
Trong tam giác vuông A'BD có .
Do đó suy ra tam giác BO'D nên .
Vậy (đvtt).
Tính đường cao
Cho hình nón đỉnh S có đáy là hình tròn tâm O, bán kính R. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng ![]() , khoảng cách từ tâm O đến mặt phẳng (SAB) bằng
, khoảng cách từ tâm O đến mặt phẳng (SAB) bằng ![]() . Đường cao h của hình nón bằng:
. Đường cao h của hình nón bằng:
Theo giả thiết ta có tam giác OAB đều cạnh R.
Gọi E là trung điểm AB, suy ra và
.
Gọi H là hình chiếu của O trên SE, suy ra .
Ta có
Từ đó suy ra nên
Trong tam giác vuông SOE, ta có
Tính bán kính mặt cầu
Bán kính mặt cầu đi qua bốn điểm ![]() và
và ![]() bằng:
bằng:
Gọi phương trình mặt cầu có dạng
với
.
Do đi qua bốn điểm M, N, P, Q nên ta có hệ phương trình:
.
Vậy
Tính thể tích khối tứ diện
Trong không gian với hệ tọa độ ![]() cho các điểm
cho các điểm ![]() trong đó
trong đó ![]() và
và ![]() . Biết mặt phẳng
. Biết mặt phẳng ![]() tiếp xúc với mặt cầu
tiếp xúc với mặt cầu ![]() Tính thể tích của khối tứ diện
Tính thể tích của khối tứ diện ![]()
+) Ta có
+) Mặt cầu có tâm
và bán kính
+) Mặt phẳng tiếp xúc với
.
+) Áp dụng BĐT Bunhiacopski ta có:
+) Dấu xảy ra
khi đó
Viết phương trình mặt phẳng
Cho mặt cầu ![]() và mặt phẳng
và mặt phẳng ![]() . Mặt phẳng tiếp xúc với
. Mặt phẳng tiếp xúc với ![]() và song song với
và song song với ![]() có phương trình là:
có phương trình là:
Mặt cầu (S) có tâm và bán kính
Gọi là mặt phẳng tiếp xúc với
và song song với
.
Vì
Mặt phẳng tiếp xúc với mặt cầu
(thỏa điều kiện)
Vậy phương trình mặt phẳng hoặc
.
Lưu ý: Nếu hình dung phác họa hình học bài toán được thì ta có thể dự đoán được có 2 mặt phẳng thỏa mãn yêu cầu đề bài.
Chọn kết luận đúng
Trong không gian ![]() , hai điểm
, hai điểm ![]() và
và ![]() . Phương trình nào sau đây là phương trình mặt cầu đường kính
. Phương trình nào sau đây là phương trình mặt cầu đường kính ![]() ?
?
Mặt cầu nhận làm đường kính, do đó mặt cầu nhận trung điểm
của
làm tâm và có bán kính
Suy ra phương trình mặt cầu cần tìm là .
Tỉ số diện tích
Cho hình trụ có hai đáy là hai hình tròn (O) và (O’), chiều cao ![]() và bán kính đáy R. Một hình nón có đỉnh là O’ và đáy là hình tròn (O;R). Tỉ số diện tích xung quanh của hình trụ và hình nón bằng:
và bán kính đáy R. Một hình nón có đỉnh là O’ và đáy là hình tròn (O;R). Tỉ số diện tích xung quanh của hình trụ và hình nón bằng:

Diện tích xung quanh của hình trụ:
(đvdt).
Kẻ đường sinh O’M của hình nón, suy ra
.
Diện tích xung quanh của hình nón: (đvdt).
Vậy .
Viết phương trình mặt cầu
Cho hình lập phương QABC.DEFG có cạnh bằng 1 có ![]() trùng với ba trục
trùng với ba trục ![]() . Viết phương trình mặt cầu
. Viết phương trình mặt cầu ![]() nội tiếp hình lập phương.
nội tiếp hình lập phương.
có tâm
là trung điểm của 3 đoạn nối trung điểm các mặt đối diện đôi một có độ dài cạnh bằng 1. Bán kính
Diện tích và Thể tích
Thiết diện qua trục hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích toàn phần và thể tích hình nón có giá trị lần lượt là:

Gọi S, O là đỉnh và tâm đường tròn đáy của hình nón,
Khi đó, ta có thiết diện qua đỉnh là tam giác SAB.
Theo đề bài, ta có tam giác SAB vuông cân tại S nên ,
Suy ra ,
và
Diện tích toàn phần của hình nón: (đvdt).
Thể tích khối nón là: (đvtt).
Tỉ số giữa thể tích
Một hình nón có đường cao bằng 9 cm nội tiếp trong một hình cầu bán kính bằng 5 cm. Tỉ số giữa thể tích khối nón và khối cầu là:

Hình vẽ kết hợp với giả thiết, ta có
Suy ra và
Thể tích khối nón (đvtt).
Thể tích khối cầu (đvtt).
Suy ra
Chọn phương trình mặt cầu
Trong không gian với hệ toạ độ ![]() , phương trình nào sau đây là phương trình mặt cầu
, phương trình nào sau đây là phương trình mặt cầu
Phương trình mặt cầu tâm bán kính
có dạng:
Vậy đáp án cần tìm là: .
Thể tích khối trụ
Mặt phẳng đi qua trục hình trụ, cắt hình trụ theo thiết diện là hình vuông cạnh bằng a. Thể tích khối trụ bằng:
Do thiết diện đi qua trục hình trụ nên ta có h=a.
Bán kính đáy . Do đó thể tích khối trụ
(đvtt).
Mệnh đề đúng
Xét các mệnh đề:
(I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn song song và cách đường thẳng ![]() cố định một khoảng không đổi là một mặt trụ.
cố định một khoảng không đổi là một mặt trụ.
(II) Hai điểm A, B cố định. Tập hợp các điểm M trong không gian mà diện tích tam giác MAB không đổi là một mặt trụ.
Trong các mệnh đề trên, mệnh đề nào đúng?
Ta xét về khái niệm Mặt trụ suy ra (I) đúng.
Diện tích tam giác MAB không đổi khi và chỉ khi khoảng cách từ M đến đường thẳng AB không đổi (giả sử bằng R ).
Vậy tập hợp các điểm M là mặt trụ bán kính R và trục là AB.
Vì vậy Mệnh đề (II) cũng đúng.
Độ dài đường sinh
Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và ![]() . Độ dài đường sinh
. Độ dài đường sinh ![]() của hình nón bằng:
của hình nón bằng:

Gọi I là trung điểm AB, suy ra và
.
Trong tam giác vuông SOA, ta có
Trong tam giác vuông SIA, ta có
Trong tam giác vuông OIA, ta có:
Tính diện tích mặt cầu (S)
Cho hình hợp chữ nhật ABCD.EFGH có ![]() . Tính diện tích mặt cầu (S) ngoại tiếp hình hợp chữ nhật.
. Tính diện tích mặt cầu (S) ngoại tiếp hình hợp chữ nhật.
Mặt cầu ngoại tiếp hình hợp chữ nhật có tâm là trung điểm chung của 4 đường chéo bằng nhau của hình hộp và có đường chéo bằng đường chéo. (Học sinh tự vẽ hình)
đvdt
Xác định phương trình mặt cầu thỏa mãn điều kiện
Phương trình mặt cầu có tâm ![]() và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là:
và cắt trục Ox tại hai điểm A, B sao cho tam giác IAB vuông là:
Gọi H là hình chiếu của trên Ox
Vậy phương trình mặt cầu là:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
