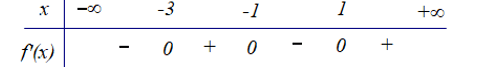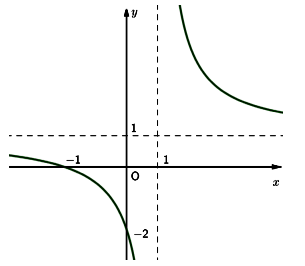Chọn mệnh đề đúng
Cho hàm số ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Cách 1.
Ta có: ;
Lập bảng biến thiên. Vậy hàm số đạt cực tiểu tại và giá trị cực tiểu bằng
.
Cách 2.
Ta có ;
. Khi đó:
;
.
Nên hàm số đạt cực tiểu tại và giá trị cực tiểu bằng
.