Mệnh đề nào sau đây đúng?
Cho các hàm số ![]() có đồ thị như hình vẽ. Đường thẳng
có đồ thị như hình vẽ. Đường thẳng ![]() cắt trục hoành, đồ thị hàm số
cắt trục hoành, đồ thị hàm số ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() . Biết rằng
. Biết rằng ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
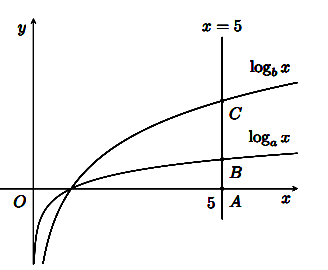
Ta có:
Theo bài ra ta có:
Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bài kiểm tra phút Chương 2: Hàm số lũy thừa - Hàm số mũ - Hàm số Logarit Toán 12 các em nhé!
Mệnh đề nào sau đây đúng?
Cho các hàm số ![]() có đồ thị như hình vẽ. Đường thẳng
có đồ thị như hình vẽ. Đường thẳng ![]() cắt trục hoành, đồ thị hàm số
cắt trục hoành, đồ thị hàm số ![]() và
và ![]() lần lượt tại
lần lượt tại ![]() . Biết rằng
. Biết rằng ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
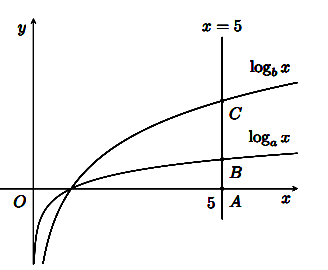
Ta có:
Theo bài ra ta có:
PT trở thành?
Nếu đặt ![]() thì phương trình
thì phương trình ![]() trở thành phương trình nào?
trở thành phương trình nào?
Đặt
PT
.
Tìm tập nghiệm của BPT mũ
Tập nghiệm của bất phương trình ![]() là:
là:
Ta có:
.
Tính giá trị của biểu thức logarit
Với các số a, b, c là các số thực dương tùy ý khác 1 và ![]() . Khi đó giá trị của
. Khi đó giá trị của ![]() bằng:
bằng:
Với a, b, c là các số thực dương tùy ý khác 1 ta có:
Khi đó ta có:
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
Cho hàm số ![]() . Cho các khẳng định sau:
. Cho các khẳng định sau:
i) Hàm số xác định với mọi x
ii) Đồ thị hàm số luôn đi qua điểm (1; 1)
iii) Hàm số nghịch biến trên ![]()
iv) Đồ thị hàm số có hai đường tiệm cận
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
Ta có khẳng định ii) và iv) là đúng
i) Sai vì hàm số đã cho xác định khi x > 0
iii) Sai vì hàm số nghịch biến trên
Đếm số nghiệm thực
Phương trình ![]() có tất cả bao nhiêu nghiệm thực ?
có tất cả bao nhiêu nghiệm thực ?
Ta có:
Xét hàm số
Ta có:
Hàm số nghịch biến trên R do các cơ số
.
Vậy phương trình có nghiệm duy nhất là x=2.
Tìm nghiệm nguyên nhỏ nhất
Nghiệm nguyên nhỏ nhất của phương trình ![]() là?
là?
3 || ba || Ba
Nghiệm nguyên nhỏ nhất của phương trình ![]() là?
là?
3 || ba || Ba
Điều kiện:
Ta có:
So điều kiện suy ra phương trình có nghiệm .
Tìm tập nghiệm PT Logarit
Phương trình ![]() có tập nghiệm là:
có tập nghiệm là:
{2} || T={2}
Phương trình ![]() có tập nghiệm là:
có tập nghiệm là:
{2} || T={2}
PT
.
Tính tổng 2 nghiệm
Gọi ![]() là 2 nghiệm của phương trình
là 2 nghiệm của phương trình ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
-3
Gọi ![]() là 2 nghiệm của phương trình
là 2 nghiệm của phương trình ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
-3
Điều kiện:
Vậy .
Định giá trị gần nhất với kết quả
Cho ![]() là ba số thực dương,
là ba số thực dương, ![]() thỏa mãn:
thỏa mãn:
![]()
Khi đó, giá trị của biểu thức ![]() gần với giá trị nào nhất sau đây?
gần với giá trị nào nhất sau đây?
Áp dụng bất đẳng thức , ta được:
Do đó với
Dấu “=” xảy ra khi
Khi đó .
Vậy giá trị của T gần 8 nhất.
Chọn đáp án thích hợp
Dựa vào thông tin dưới đây và trả lời các câu hỏi
Số lượng của một loại vi khuẩn X trong một phòng thí nghiệm được biểu diễn theo công thức ![]() , trong đó A là số lượng vi khuẩn tại thời điểm chọn mốc thời gian, r là tỉ lệ tăng trưởng (r > 0), t là thời gian tăng trưởng (tính theo đơn vị là giờ). Lúc 6 giờ sáng, số lượng vi khuẩn X là 150 con. Sau 3 giờ, số lượng vi khuẩn X là 450 con.
, trong đó A là số lượng vi khuẩn tại thời điểm chọn mốc thời gian, r là tỉ lệ tăng trưởng (r > 0), t là thời gian tăng trưởng (tính theo đơn vị là giờ). Lúc 6 giờ sáng, số lượng vi khuẩn X là 150 con. Sau 3 giờ, số lượng vi khuẩn X là 450 con.
Tỉ lệ tăng trưởng của vi khuẩn X gần nhất với kết quả nào sau đây?
Chọn 6 giờ là mốc thời gian. Khi đó .
Sau 3 giờ, số lượng vi khuẩn là 450 con nên .
Từ đó ta có phương trình:
Tổng 2 nghiệm PT mũ
Gọi ![]() là hai nghiệm của phương trình
là hai nghiệm của phương trình ![]() . Khi đó, tổng hai nghiệm bằng?
. Khi đó, tổng hai nghiệm bằng?
Ta có:
Đặt , phương trình trên tương đương với:
(vì
).
Từ đó suy ra
Vậy tổng hai nghiệm bằng 0.
Nghiệm nguyên lớn nhất
Nghiệm nguyên lớn nhất của bất phương trình ![]() là:
là:
x=1 || X=1 || x bằng 1
Nghiệm nguyên lớn nhất của bất phương trình ![]() là:
là:
x=1 || X=1 || x bằng 1
Vậy nghiệm nguyên lớn nhất của BPT là .
Khẳng định nào sau đây là đúng?
Cho biểu thức ![P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6}](/data/image/holder.png) với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
với a và b là các số thực dương. Khẳng định nào sau đây là đúng?
Thực hiện thu gọn biểu thức như sau:
Tính giá trị biểu thức
Tính giá trị của ![]() với
với ![]()
Ta có:
Khẳng định nào sau đây đúng?
Cho các số thực dương a, b với ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Trường hợp 1:
Trường hợp 2:
Vậy
Tìm điều kiện xác định
Điều kiện xác định của bất phương trình ![]() là:
là:
BPT xác định khi: .
Tìm m để đồ thị hàm số thỏa mãn điều kiện
Đồ thị hàm số ![]() có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
có điểm cực tiểu và điểm cực đại nằm về hai phía trục tung khi:
Ta có:
Đồ thị có điểm cực đại và cực tiểu khi và chỉ khi y’ = 0 có hai nghiệm
Theo định lí Vi – et ta có:
Hai điểm cực trị nằm về hai phía trục tung khi và chỉ khi
Tính giá trị nhỏ nhất của biểu thức
Cho ![]() thỏa mãn
thỏa mãn ![]() . Khi đó giá trị nhỏ nhất của biểu thức
. Khi đó giá trị nhỏ nhất của biểu thức ![]() là:
là:
Ta có:
Đặt . Ta có:
thỏa mãn
Ta lại có
Xét hàm số
Vậy giá trị nhỏ nhất của biểu thức là khi
Tìm nghiệm nguyên lớn nhất
Nghiệm nguyên lớn nhất của bất phương trình là:
x=7 || X=7 || x bằng 7 || 7
Nghiệm nguyên lớn nhất của bất phương trình là:
x=7 || X=7 || x bằng 7 || 7
Điều kiện:
Ta có:
.
Vậy nghiệm nguyên lớn nhất của bất phương trình là: .
Chọn khẳng định đúng?
Anh T đã làm hợp đồng xin vay vốn ngân hàng để kinh doanh với số tiền 200 triệu đồng với lãi suất a% trên một năm. Điều kiện hợp đồng là số tiền lại tháng trước sẽ được tính làm vốn để sinh lãi cho tháng sau. Sau hai năm kinh doanh, anh T dã thanh toán hợp đồng ngân hàng với số tiền làm tròn là 245512000 đồng. Chọn khẳng định đúng?
Lãi suất mỗi tháng là . Theo công thức lãi kép ta có:
Tính giá trị của biểu thức
Cho ![]() . Biết
. Biết ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức ![]()
Hàm số f(x) xác định trên tập số thực
Đặt hàm số g(x) cũng có tập xác định
Dễ thấy ta có:
Vậy hàm số g(x) là hàm số lẻ trên tập số thực.
Ta thấy
Đặt
Theo giả thiết ta có: từ (*) ta có:
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
Hàm số nào sau đây nghịch biến trên tập xác định của nó?
Ta có: nên hàm số nghịch biến trên tập xác định của nó.
Rút gọn biểu thức P
Rút gọn biểu thức ![P = \frac{{{x^{\frac{1}{6}}}.\sqrt[3]{{{x^4}}}.\sqrt[4]{{{x^5}}}}}{{\sqrt {{x^3}} }}](/data/image/holder.png) với x > 0
với x > 0
Ta có:
Xác định giá trị của biểu thức logarit
Với các số a, b > 0 thỏa mãn ![]() , biểu thức
, biểu thức ![]() bằng:
bằng:
Ta có:
Chọn khẳng định đúng?
Cho biết ![]() với
với ![]() . Chọn khẳng định đúng?
. Chọn khẳng định đúng?
Ta có:
Vậy
Tìm tập xác định của hàm số
Tìm tập xác định của hàm số ![]() là:
là:
Hàm số đã cho xác định khi
Giá trị của biểu thức
Giá trị của biểu thức ![]()
Ta có:
Khẳng định nào dưới đây đúng?
Cho ![]() và khác 1. Các hàm số
và khác 1. Các hàm số ![]() có đồ thị như hình vẽ bên. Khẳng định nào dưới đây đúng?
có đồ thị như hình vẽ bên. Khẳng định nào dưới đây đúng?
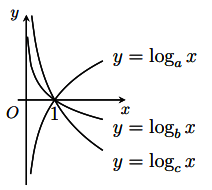
Kẻ đường thẳng cắt đồ thị các hàm số
lần lượt tại các điểm có hoành độ

Từ đồ thị ta có:
Rút gọn biểu thức T
Thu gọn biểu thức ![T = \frac{{{a^{\frac{7}{6}}}.{b^{ - \frac{2}{3}}}}}{{\sqrt[6]{{a{b^2}}}}}](/data/image/holder.png) biết a và b là hai số thực dương.
biết a và b là hai số thực dương.
Ta có:
Tìm tập xác định của hàm số
Tập xác định của hàm số ![]() là tập hợp nào sau đây?
là tập hợp nào sau đây?
Điều kiện xác định
Vậy tập xác định của hàm số là
Đạo hàm bậc nhất của hàm lũy thừa
Cho hàm số ![]() . Tính
. Tính ![]()
Tập xác định
Ta có:
Tập xác định của hàm số y
Tập xác định của hàm số ![]() là:
là:
Điều kiện xác định:
=> Tập xác định của hàm số là
Tính giá trị biểu thức T
Cho ![]() , viết
, viết ![]() về dạng
về dạng ![]() và
và ![]() về dạng
về dạng ![]() . Tình giá trị biểu thức
. Tình giá trị biểu thức ![]()
Ta có:
Tìm điều kiện của x để hàm số có nghĩa?
Tìm điều kiện của x để hàm số ![]() có nghĩa?
có nghĩa?
Ta có điều kiện xác định
Phương trình tiếp tuyến của đồ thị hàm số
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
Ta có:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm thuộc đồ thị hàm số có hoành độ bằng 1 là:
Trong các khẳng định sau, khẳng định nào đúng?
Trong các khẳng định sau, khẳng định nào đúng?
Xét hàm số ta có:
Vậy hàm số đồng biến trên tập số thực.
Trong các phát biểu sau đây, phát biểu nào sai?
Trong các phát biểu sau đây, phát biểu nào sai?
Phát biểu sai là: Hàm số mũ có tập xác định là
Sửa lại: Hàm số mũ có tập xác định là
Khẳng định nào sau đây sai?
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Hàm số có các tính chất như sau:
Đồ thị hàm số nhận trục tung làm tiệm cận đứng
Đồ thị hàm số nhận trục hoành làm tiệm cận ngang
Là hàm số nghịch biến trên
Tính đạo hàm hàm số lũy thừa
Cho hàm số ![]() . Tính
. Tính ![]()
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
