Định nghĩa và tính chất của tích phân
Bộ tài liệu Lí thuyết toán 12: Tích phân bao gồm định nghĩa, tính chất tích phân và các bài tập ứng dụng có hướng dẫn chi tiết, được xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.
1.Khái niệm tích phân
1.1. Định nghĩa
Cho 
\(f (x)\) là hàm số liên tục trên đoạn \([a;b]\). Giả sử \(F (x)\) là một nguyên hàm của \(f (x)\) trên \([a;b]\).
Hiệu số \(F(b)-F(a)\) được gọi là tích phân từ \(a\) đến \(b\) (hay tích phân xác định trên đoạn \([a;b]\) của hàm số \(f(x)\) , kí hiệu là \(\int_a^b f(x)dx\)
Ta dùng kí hiệu \(\left.F(x)\right|_a^b=F(b)-F(a)\) để chỉ hiệu số \(F(b)-F(a)\).
Vậy:
\(\int_a^b f(x)dx=\left.F(x)\right|_a^b=F(b)-F(a)\)
Trong đó: \(\int_a^b\) là dấu tích phân, \(a\) là cận dưới, \(b\) là cận trên
\(f (x) dx\) là biểu thức dưới dấu tích phân, \(f (x)\) là hàm số dưới dấu tích phân
Ví dụ:
a) \(\int_1^2 3xdx=\left.x^3\right|_1^2= 2^3-1^3=7\)
Vậy Tích phân của hàm số \(3x\) đi từ 1 đến 2 là bằng \(7\).
b) \(\int\limits_0^1 {\frac{1}{{x + 1}}dx} = \left. {\left( {\ln \left| {x + 1} \right|} \right)} \right|_0^1 = \ln 2\)
Vậy Tích phân của hàm số \(\frac{1}{{x + 1}}\) đi từ 0 đến 1 là bằng \(ln2\).
1.2. Nhận xét
Tích phân của hàm số \(f\) từ \(a\) đến \(b\) có thể kí hiệu bởi \(\int_a^b f(x)dx\) hay \(\int_a^b f(t)dt\).
Tích phân đó chỉ phụ thuộc vào các cận mà không phụ thuộc vào cách ghi biến số.
1.3. Ý nghĩa hình học của tích phân
Nếu hàm số \(f (x)\) liên tục và không âm trên đoạn \([a;b]\) thì tích phân \(\int_a^b f(x)dx\) là diện tích \(S\) của hình thang cong giới hạn bởi đồ thị hàm số \(y=f(x)\), trục \(Ox\) và hai đường thẳng \(x=a,x=b\).
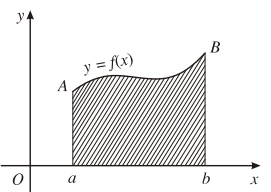
Vậy \(S=\int_a^b f(x)dx\).
2.Tính chất của tích phân
Tính chất 1: Tích phân tại 1 giá trị xác định của biến số thì bằng 0
\(\int_a^a f(x)dx=0\)
Chứng minh:
\(\int_a^a f(x)dx=\left.F(x)\right|_a^a=F(a)-F(a) =0\)
Tính chất 2: Đảo cận thì đổi dấu
\(\int_a^b f(x)dx=-\int_b^af(x)dx\)
Chứng minh:
Ta có:
\(\int_a^b f(x)dx=\left.F(x)\right|_a^b=F(b)-F(a)\)
\(\int_b^a f(x)dx=\left.F(x)\right|_b^a=F(a)-F(b)\)
\(\Rightarrow - \int_b^a f(x)dx= -(F(a)-F(b))=F(b)-F(a)\)
Vậy \(\int_a^b f(x)dx=-\int_b^af(x)dx\)
Tính chất 3: Cộng hai tích phân
\(\int_a^c f (x)dx + \int_c^b f (x)dx = \int_a^b f (x)dx\) ; \((a < c < b )\)
Chứng minh:
Giả sử \(F (x)\) là một nguyên hàm của \(f (x)\) trên \([a;b]\). Khi đó \(F (x)\) cũng là một nguyên hàm của \(f (x)\) trên \([a;c]\) và \([c;b]\) với \((a < c < b )\)
Suy ra
\(\begin{matrix}
\int_a^c f (x)dx + \int_c^b f (x)dx \hfill \\
= \left[ {F\left( c \right) - F\left( a \right)} \right] + \left[ {F\left( b \right) - F\left( c \right)} \right] \hfill \\
= F\left( b \right) - F\left( a \right) = \int_a^b f (x)dx \hfill \\
\end{matrix}\)
Vậy \(\int_a^c f (x)dx + \int_c^b f (x)dx = \int_a^b f (x)dx\); \((a < c < b )\)
Tính chất 4: Hằng số trong tích phân có thể được đưa ra ngoài dấu tích phân
\(\int_a^b k\cdot f(x)dx=k\cdot\int_a^b f(x)dx(k\in \mathbb{R})\)
Chứng minh:
Nếu \(k=0\) thì Tính chất 4 luôn đúng
Nếu \(k \neq 0\) thì \(\int k\cdot f(x)dx=k\cdot\int f(x)dx = F(x) \,\,(k\in \mathbb{R}) \Rightarrow
\int f(x)dx = \dfrac{F(x)}{k}\)
Do đó, ta có: \(\int_a^b k.f(x)dx=\left.F(x)\right|_a^b=F(b)-F(a)\)
Mặt khác, ta được \(k \int_a^b f(x)dx=\left.k\dfrac{F(x)}{k}\right|_a^b=F(b)-F(a)\)
Vậy \(\int_a^b k\cdot f(x)dx=k\cdot\int_a^b f(x)dx(k\in \mathbb{R})\).
Tính chất 5: Tích phân của 1 tổng thì bằng tổng các tích phân
\(\int_a^b[f(x)\pm g(x)]dx=\int_a^b f(x)dx±\int_a^b g(x)dx.\)
Chứng minh:
Giả sử F(x) và G(x) lần lượt là các nguyên hàm của f(x) và g(x).
Ta có
\(\int [f(x)\pm g(x)]dx=\int f(x)dx±\int g(x)dx=F(x)\pm G(x).\)
Do đó
\(\int_a^b [f(x)\pm g(x)]dx=[F(x)\pm G(x)]|_a^b\)
\(= [F(b)\pm G(b)] -[F(a)\pm G(a)] =[F(b)-F(a)] \pm [ G(b)-G(a)]\) (1)
Ta xét \(\int_a^b f(x)dx±\int_a^b g(x)dx = F(x)|_a^b \pm G(x)|_a^b\)
\(=[F(b)-F(a)] \pm [ G(b)-G(a)]\) (2)
Từ (1) và (2) ta có đpcm!
Một số ví dụ tính tích phân đơn giản:
a) \(I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} \right)dx}\)
Giải:
\(I = \int\limits_1^2 {\left( {\frac{1}{{{x^2}}} + 2x} \right)dx} = \left. {\left( { - \frac{1}{x} + {x^2}} \right)} \right|_1^2 = \frac{7}{2}\)
b) \(I = \int\limits_{ - 1}^1 {\left( {{x^3} + 3x + 2} \right)dx}\)
Giải:
\(I = \int\limits_{ - 1}^1 {\left( {{x^3} + 3x + 2} \right)dx} = \left. {\left( {\frac{1}{4}{x^4} + \frac{3}{2}{x^2} + 2x} \right)} \right|_{ - 1}^1 = 4\)
c) \(I = \int\limits_1^2 {\left( {{x^2} + \frac{x}{{x + 1}}} \right)dx}\)
Giải:
\(I = \int\limits_1^2 {\left( {{x^2} + \frac{x}{{x + 1}}} \right)dx} = \int\limits_1^2 {\left( {{x^2} + 1 - \frac{1}{{x + 1}}} \right)dx}\)
\(= \left. {\left( {\frac{{{x^3}}}{3} + x - \ln \left| {x + 1} \right|} \right)} \right|_1^2\)
\(= \frac{8}{3} + 2 - \ln 3 - \left( {\frac{1}{3} + 1 - \ln 2} \right) = \frac{{10}}{3} + \ln 2 - \ln 3\)
