Đồ thị hàm số
Bài học Lí thuyết toán 12: Đồ thị hàm số đã giới thiệu cho các em sơ đồ khảo sát hàm số, các bước khảo sát hàm đa thức, hàm phân thức. Bên cạnh đó là một số ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.
1. Sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số
Bước 1: Tập xác định
- Tìm tập xác định của hàm số.
Bước 2: Sự biến thiên của hàm số
- Tìm các giới hạn tại vô cực, các giới hạn vô cực và tiệm cận (nếu có).
- Xét chiều biến thiên của hàm số:
- Tính đạo hàm. Tìm các điểm tại đó đạo hàm bằng 0 hoặc không xác định.
- Lập bảng biến thiên và kết luận khoảng đồng biến, nghịch biến và cực trị của hàm số.
Bước 3: Đồ thị
- Dựa vào bảng biến thiên và các yếu tố xác định ở trên để vẽ đồ thị.
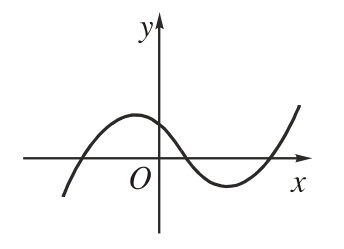
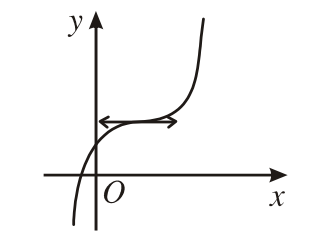
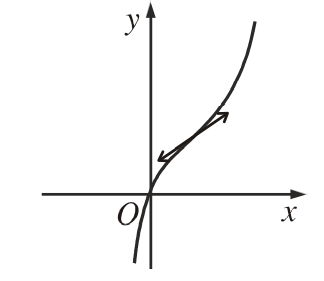
2. Đồ thị hàm số bậc ba: 
\(y = a{x^3} + b{x^2} + cx + d{\text{ }}(a \ne 0)\)
Các dạng đồ thị của hàm số bậc 3:
|
|
\(a > 0\) |
\(a < 0\) |
|
Phương trình
có hai nghiệm phân biệt |
|
 |
|
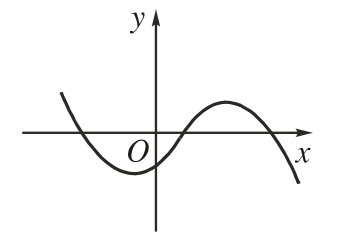Phương trình
có nghiệm kép |
|
 |
|
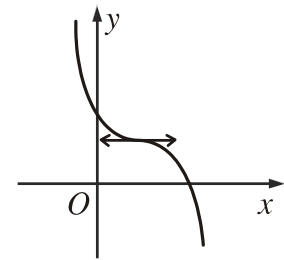Phương trình
vô nghiệm |
|
 |
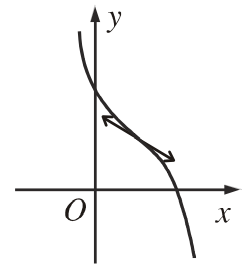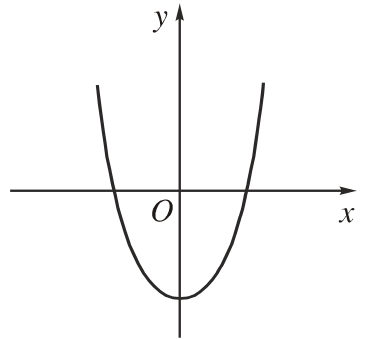
3. Đồ thị hàm số bậc bốn trùng phương: \(y = a{x^4} + b{x^2} + c{\text{ }}(a \ne 0)\)
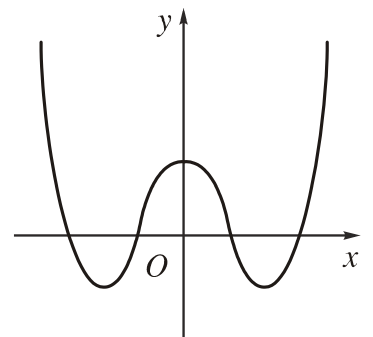
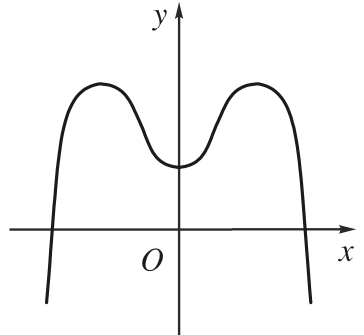
Các dạng đồ thị của hàm số bậc 4 trùng phương:
|
|
|
|
|
có 1 nghiệm
|
|
 |
|
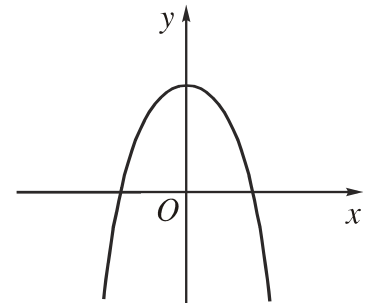có 3 nghiệm
|
 |
 |
4. Đồ thị của hàm số \(y = \frac{{ax + b}}{{cx + d}}{\text{ }}(c \ne 0,ad - bc \ne 0)\)
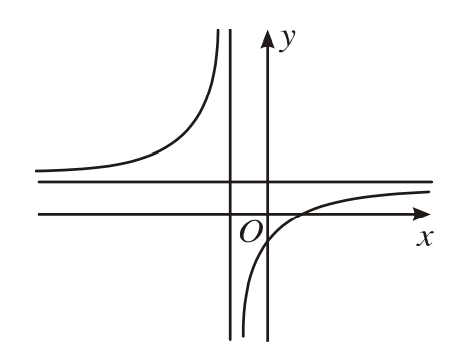
Các dạng đồ thị hàm phân thức:
| \(D=ad-bc > 0\) |
\(D=ad - bc < 0\) |
 |
 |
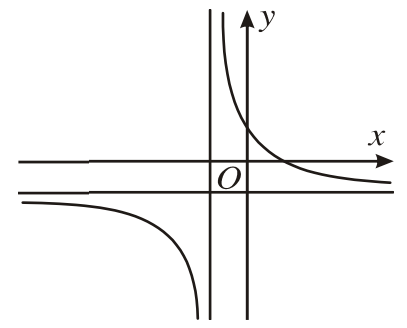Chú ý: Từ đồ thị đã cho, ta suy ra chiều biến thiên, lập bảng biến thiên trong mỗi trường hợp và chỉ ra các đường tiệm cận của đồ thị
5. Các phép biến đổi đồ thị
Cho hàm số \(y = f(x)\) có đồ thị \((C)\). Khi đó với số \(a > 0\), ta có:
- Hàm số \(y = f(x) +a\) có đồ thị \((C')\) bằng cách tịnh tiến đồ thị \((C)\) theo phương \(Oy\) lên trên \(a\) đơn vị.
- Hàm số \(y = f(x) - a\) có đồ thị \((C')\) bằng cách tịnh tiến đồ thị \((C)\) theo phương \(Oy\) xuống dưới \(a\) đơn vị.
- Hàm số \(y = f(x + a)\) có đồ thị \((C')\) bằng cách tịnh tiến đồ thị \((C)\) theo phương \(Ox\) sang trái \(a\) đơn vị.
- Hàm số \(y = f(x - a)\) có đồ thị \((C')\) bằng cách tịnh tiến đồ thị \((C)\) theo phương \(Ox\) sang phải \(a\) đơn vị.
- Hàm số \(y = - f(x)\)có đồ thị \((C')\) là đối xứng của đồ thị \((C)\) qua trục \(Ox\).
- Hàm số \(y = f( - x)\) có đồ thị \((C')\) là đối xứng của đồ thị \((C)\) qua trục \(Oy\).
- Hàm số \(y = f\left( {\left| x \right|} \right) = \left\{ \begin{gathered}
f(x){\text{ }}khi{\text{ }}x \geqslant 0 \hfill \\
f( - x){\text{ }}khi{\text{ }}x < 0 \hfill \\
\end{gathered} \right.\) có đồ thị \((C')\) suy từ đồ thị \((C)\) bằng cách:
- Giữ nguyên phần đồ thị \((C)\) nằm bên phải trục \(Oy\) và bỏ phần đồ thị \((C)\) nằm bên trái \(Oy\).
- Lấy đối xứng phần đồ thị \((C)\) nằm bên phải \(Oy\) qua \(Oy\).
- Hàm số \(y = \left| {f(x)} \right| = \left\{ \begin{gathered}
f(x){\text{ }}khi{\text{ }}f(x) \geqslant 0 \hfill \\
- f(x){\text{ }}khi{\text{ }}f(x) < 0 \hfill \\
\end{gathered} \right.\) có đồ thị \((C')\) suy từ đồ thị \((C)\) bằng cách:
- Giữ nguyên phần đồ thị \((C)\) nằm phía trên trục hoành.
- Lấy đối xứng phần đồ thị \((C)\) nằm bên phía dưới trục hoành và đối xứng qua trục hoành
- Cuối cùng, ta bỏ phần đồ thị \((C)\) nằm dưới \(Ox\).
