Phương trình mặt phẳng
Bài học Lí thuyết toán 12: Phương trình mặt phẳng bao gồm khái niệm VTPT, phương trình tổng quát mặt phẳng và các trường hợp riêng, đặc biệt. Bên cạnh đó, bài học kèm theo một số ví dụ bài tập có hướng dẫn giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia. Hi vọng các em sẽ ôn tập hiệu quả, hướng đến đạt mục tiêu trong các kì thi lớn sắp tới.
1. Vectơ pháp tuyến của mặt phẳng
Cho mặt phẳng 
\((\alpha )\). Vectơ \(\overrightarrow n \ne \overrightarrow 0\) là vectơ pháp tuyến (VTPT) nếu giá của \(\vec n\) vuông góc với mặt phẳng \((\alpha )\)
Chú ý:
- Nếu \(\vec n\) là một VTPT của mặt phẳng \((\alpha )\) thì \(k \vec n \,\,\, (k \neq 0)\) cũng là một VTPT của mặt phẳng \((\alpha )\).
- Một mặt phẳng được xác định duy nhất nếu biết một điểm nó đi qua và một VTPT của nó.
- Nếu \(\overrightarrow u ,\,\overrightarrow v\)có giá song song hoặc nằm trên mặt phẳng \((\alpha )\) thì là một VTPT của \((\alpha )\).
Ví dụ: Mặt phẳng \((\alpha ) : x-5y+6z-2022=0\) có một vecto pháp tuyến là \(\vec n(1; -5;6)\)
2. Phương trình tổng quát của mặt phẳng
Trong không gian \(Oxyz\), mọi mặt phẳng đều có dạng phương trình:
\(Ax + By + Cz + D = 0\,\,\) với \({A^2} + {B^2} + {C^2} \ne 0\)
Phương trình đó được gọi là phương trình tổng quát của mặt phẳng.
Nhận xét:
- Nếu mặt phẳng \((\alpha )\) có phương trình \(Ax + By + Cz + D = 0\,\,\) thì nó có một VTPT là \(\overrightarrow n (A;\,B;\,C)\).
- Phương trình mặt phẳng đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và nhận vectơ \(\overrightarrow n (A;\,B;\,C)\) khác \(\vec 0\) là VTPT là: \(A(x - {x_0}) + B(y - {y_0}) + C(z - {z_0}) = 0\).
Ví dụ: Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) đi qua điểm \(A(1;0; - 2)\) và có vectơ pháp tuyến \(\overrightarrow n (1; - 1;2)\).
Giải:
Mặt phẳng \((P)\) đi qua điểm \(A(1;0; - 2)\) và có vectơ pháp tuyến \(\overrightarrow n (1; - 1;2)\) có phương trình là:
\(\,1(x - 1) - 1(y - 0) + 2(z + 2) = 0\) \(\Leftrightarrow \,\,x - y + 2z + 3 = 0\)
Vậy phương trình mặt phẳng \((P)\) là: \(x - y + 2z + 3 = 0\).
Các trường hợp riêng:
Xét phương trình mặt phẳng \((\alpha )\): \(Ax + By + Cz + D = 0\,\,\) với \({A^2} + {B^2} + {C^2} \ne 0\)
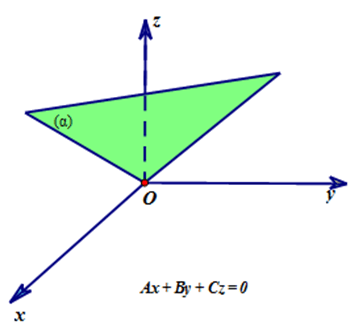
- Nếu \(D=0\) thì mặt phẳng \((\alpha )\) đi qua gốc tọa độ O.
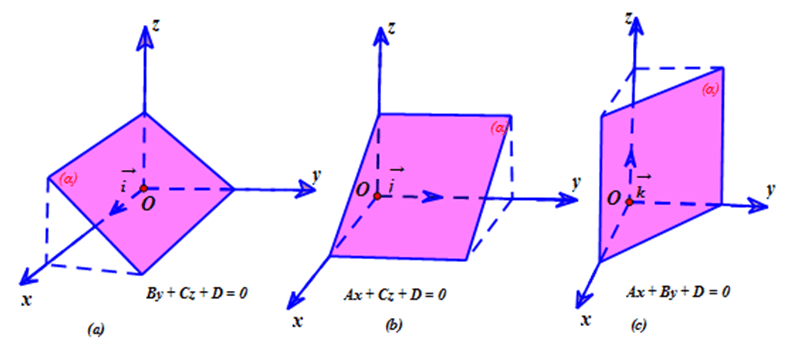
- Nếu \(A = 0,B \ne 0,C \ne 0\) thì mặt phẳng \((\alpha )\) song song hoặc chứa trục \(Ox\).
- Nếu \(A \ne 0,B = 0,C \ne 0\) thì mặt phẳng \((\alpha )\) song song hoặc chứa trục \(Oy\).
- Nếu \(A \ne 0,B \ne 0,C = 0\) thì mặt phẳng \((\alpha )\) song song hoặc chứa trục \(Oz\).
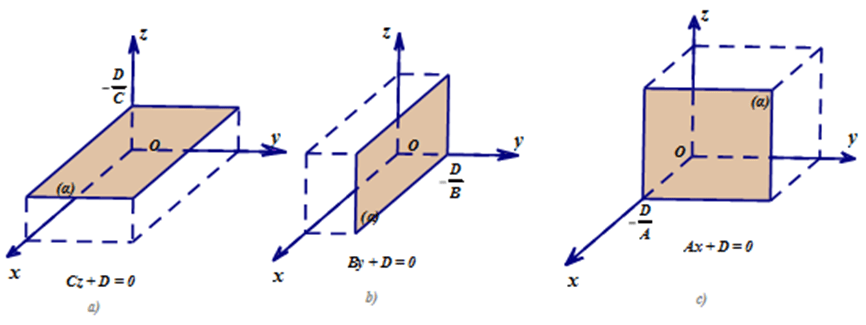
- Nếu \(A = B = 0,C \ne 0\) thì mặt phẳng \((\alpha )\) song song hoặc trùng với \((Oxy)\).
- Nếu \(A = C = 0,B \ne 0\) thì mặt phẳng \((\alpha )\) song song hoặc trùng với \((Oxz)\).
- Nếu \(B = C = 0,A \ne 0\) thì mặt phẳng \((\alpha )\) song song hoặc trùng với \((Oyz)\).
Chú ý:
- Nếu trong phương trình \((\alpha )\) không chứa ẩn nào thì \((\alpha )\) song song hoặc chứa trục tương ứng.
- Phương trình mặt phẳng theo đoạn chắn \(\left( \alpha \right):\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\).
Ở đây \((\alpha )\) cắt các trục tọa độ tại các điểm \(\left( {a;0;0} \right)\), \(\left( {0;b;0} \right)\),\(\left( {0;0;c} \right)\) với \(abc \ne 0\).
Ví dụ: Trong không gian \(Oxyz\), viết phương trình mặt phẳng đi qua ba điểm \(A(1;0; - 2),\,\,B(1;1;1),\,\,C(0; - 1;2)\).
Giải:
Ta có: \(\overrightarrow {AB} = (0;1;3),\overrightarrow {AC} = ( - 1; - 1:4)\)
\(\Rightarrow \left[ {\overrightarrow {AB} ,\overrightarrow {AC} \,} \right] = (7; - 3;1)\).
Gọi \(\vec n\) là một vectơ pháp tuyến của mặt phẳng \((ABC)\) ta có \(\left\{ {\begin{array}{*{20}{c}}
{\overrightarrow n \bot \overrightarrow {AB} } \\
{\overrightarrow n \bot \overrightarrow {AC} }
\end{array}} \right.\)
nên \(\vec n\) cùng phương với \(\left[ {\overrightarrow {AB} ,\overrightarrow {AC} \,} \right]\).
Chọn \(\overrightarrow n = (7; - 3;1)\) ta được phương trình mặt phẳng \((ABC)\) là:
\(7(x - 1) - 3(y - 0) + 1(z + 2) = 0\)
\(\Leftrightarrow 7x - 3y + z - 5 = 0\)
Vậy phương trình mp cần tìm là \((ABC): 7x - 3y + z - 5 = 0\).
