Mặt cầu
Bài học Lí thuyết toán 12: Mặt cầu bao gồm định nghĩa mặt cầu, vị trí tương đối, công thức tính diện tích, thể tích mặt cầu. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết, xây dựng dựa trên kiến thức trọng tâm chương trình Toán 12 và các câu hỏi trong đề thi THPT Quốc gia.
1. Khái niệm mặt cầu
1.1. Định nghĩa
Tập hợp các điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng R 
\((R > 0)\) gọi là mặt cầu tâm O, bán kính R.
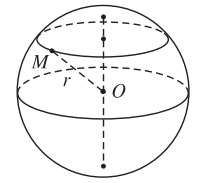
- Kí hiệu là: \(S\left( {O;{\text{R}}} \right)\).
- Khi đó \(S\left( {O;{\text{R}}} \right) = \left\{ {M|OM = R} \right\}\)
1.2. Biểu diễn mặt cầu:
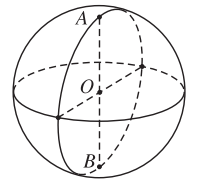
- Sử dụng phép chiếu vuông góc đề biểu diễn mặt cầu. Khi đó, hình biểu diễn của mặt cầu là một hình tròn.
- Ứng dụng của hình biểu diễn mặt cầu là đường kinh tuyến và vĩ tuyến của mặt cầu.
2. Vị trí tương đối
2.1. Vị trí tương đối của một điểm đối với mặt cầu
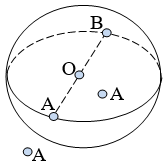
Cho mặt cầu \(S\left( {O;{\text{R}}} \right)\) và một điểm A bất kì, khi đó:
- Nếu \(OA = {\text{R}} \Leftrightarrow A \in S\left( {O;{\text{R}}} \right)\). Khi đó \(OA\) gọi là bán kính mặt cầu. Nếu \(OA\) và \(OB\) là hai bán kính sao cho \(\overrightarrow {OA} = - \overrightarrow {OB}\) thì đoạn thẳng \(AB\) gọi là một đường kính của mặt cầu.
- Nếu \(OA < {\text{R}} \Leftrightarrow A\) nằm trong mặt cầu.
- Nếu \(OA > {\text{R}} \Leftrightarrow A\) nằm ngoài mặt cầu.
\(\Rightarrow\) Khối cầu \(S\left( {O;{\text{R}}} \right)\) là tập hợp tất cả các điểm M sao cho \(OM \leqslant {\text{R}}\).
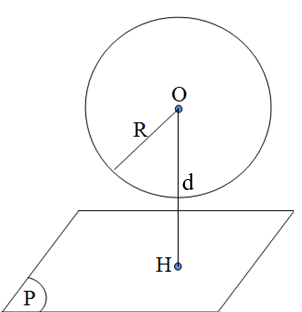
2.2. Vị trí tương đối của mặt phẳng và mặt cầu
Cho mặt cầu \(S\left( {O;{\text{R}}} \right)\) và một \(mp\left( P \right)\). Gọi d là khoảng cách từ tâm O của mặt cầu đến \(mp\left( P \right)\) và H là hình chiếu của O trên \(mp\left( P \right)\) \(\Rightarrow d = OH\).
- Nếu \(d < R \Leftrightarrow\) \(mp\left( P \right)\) cắt mặt cầu \(S\left( {O;{\text{R}}} \right)\) theo giao tuyến là đường tròn nằm trên \(mp\left( P \right)\) có tâm là H và bán kính \(r = HM = \sqrt {{R^2} - {d^2}} = \sqrt {{R^2} - O{H^2}}\)
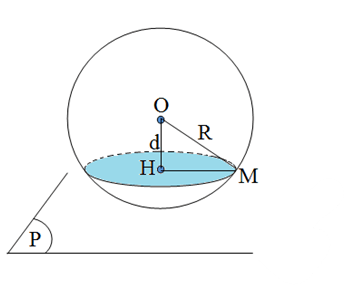
- Nếu \(d > R \Leftrightarrow mp\left( P \right)\) không cắt mặt cầu \(S\left( {O;{\text{R}}} \right)\).
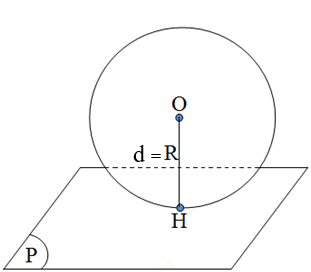
- Nếu \(d = R \Leftrightarrow mp\left( P \right)\) có một điểm chung duy nhất. Ta nói mặt cầu \(S\left( {O;{\text{R}}} \right)\) tiếp xúc \(mp\left( P \right)\). Do đó, điều kiện cần và đủ để \(mp\left( P \right)\) tiếp xúc với mặt cầu \(S\left( {O;{\text{R}}} \right)\) là \(d\left( {O,\left( P \right)} \right) = R\) .
2.3. Vị trí tương đối của đường thẳng và mặt cầu
Cho mặt cầu \(S\left( {O;{\text{R}}} \right)\) và một đường thẳng \(\Delta\). Gọi H là hình chiếu của O trên đường thẳng \(\Delta\) và \(d=OH\) là khoảng cách từ tâm O của mặt cầu đến đường thẳng \(\Delta\). Khi đó:
- Nếu \(d > R \Leftrightarrow \Delta\) không cắt mặt cầu \(S\left( {O;{\text{R}}} \right)\).
- Nếu \(d < R \Leftrightarrow \Delta\) cắt mặt cầu \(S\left( {O;{\text{R}}} \right)\) tại hai điểm phân biệt.
- Nếu \(d = R \Leftrightarrow \Delta\) và mặt cầu tiếp xúc nhau (tại một điểm duy nhất). Do đó: điều kiện cần và đủ để đường thẳng \(\Delta\) tiếp xúc với mặt cầu là \(d = d\left( {O,\Delta } \right) = R\).
Định lí: Nếu điểm A nằm ngoài mặt cầu \(S\left( {O;{\text{R}}} \right)\) thì:
- Qua A có vô số tiếp tuyến với mặt cầu \(S\left( {O;{\text{R}}} \right)\).
- Độ dài đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
- Tập hợp các điểm này là một đường tròn nằm trên mặt cầu \(S\left( {O;{\text{R}}} \right)\).
Ví dụ:
Một đường thẳng thay đổi d qua A và tiếp xúc với mặt cầu \(S\left( {O;{\text{R}}} \right)\) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. Độ dài đoạn thẳng MH tính theo R là?
Giải:
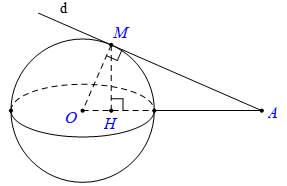
Trong mặt phẳng \((d, O)\), xét tam giác \(OMA\) vuông tại M có MH là đường cao. Ta có:
\(M{H^2} = HO.HA \Rightarrow M{H^2} = \frac{R}{2}.\frac{{3R}}{2} \Rightarrow MH = \frac{{R\sqrt 3 }}{2}\)
3. Diện tích và thể tích mặt cầu
Cho mặt cầu \(S\left( {O;{\text{R}}} \right)\), ta có các công thức tính:
- Diện tích mặt cầu:
\(\boxed{{S_C} = 4\pi {R^2}}\)
- Thể tích mặt cầu:
\(\boxed{{V_C} = \frac{4}{3}\pi {R^3}}\)
Ví dụ 1: Thể tích của một khối cầu là \(113\frac{1}{7}\,{\text{c}}{{\text{m}}^3}\) thì bán kính nó là bao nhiêu? (lấy \(\pi \approx \frac{{22}}{7}\))
Giải:
Thể tích khối cầu bán kính R là:
\(V = \dfrac{4}{3}\pi {R^3} \Rightarrow {R^3} = \dfrac{{3V}}{{4\pi }} = \dfrac{{3.113\dfrac{1}{7}}}{{4.\dfrac{{22}}{7}}} = 27 \Rightarrow R = 3\) (cm).
Ví dụ 2: (Khinh khí cầu) Nhà Mông-gôn-fie (Montgolfier) (người Pháp) phát minh ra khinh khí cầu dùng khí nóng. Coi khinh khí cầu này là một mặt cầu có đường kính \(11m\) thì diện tích của mặt khinh khí cầu là bao nhiêu? (lấy \(\pi \approx \frac{{22}}{7}\) và làm tròn kết quả đến chữ số thập phân thứ hai).
Giải:
Áp dụng công thức, ta có diện tích của kinh khí cầu là:
