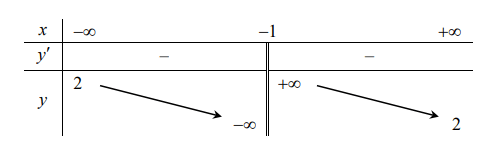
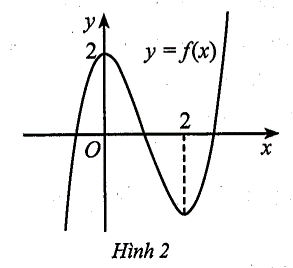
Tìm số phần tử tập S
Cho hàm số ![]() với
với ![]() là tham số. Gọi
là tham số. Gọi ![]() là tập hợp tất cả các giá trị nguyên của
là tập hợp tất cả các giá trị nguyên của ![]() để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của
để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của ![]() .
.
;
Hàm số nghịch biến trên các khoảng xác định khi
.
Mà nên có
giá trị thỏa mãn.