Chọn đáp án đúng
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số ![]() đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây?
Ta có:
Vậy hàm số đồng biến trên các khoảng
Suy ra hàm số đồng biến trên khoảng
.
Mời các bạn học cùng thử sức với đề Đề thi giữa học kì 1 môn Toán lớp 12 nha!
Chọn đáp án đúng
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số ![]() đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây?
Ta có:
Vậy hàm số đồng biến trên các khoảng
Suy ra hàm số đồng biến trên khoảng
.
Chọn đáp án đúng
Cho hàm số ![]() có đồ thị là
có đồ thị là ![]() . Số điểm thuộc
. Số điểm thuộc ![]() có hoành độ và tung độ đều là các số nguyên là
có hoành độ và tung độ đều là các số nguyên là
Ta có:
Gọi
Vậy có 4 điểm thỏa mãn yêu cầu.
Xác định hàm số đồng biến trên R
Hàm số nào sau đây đồng biến trên ![]() ?
?
Hàm số có
Tìm đáp án thích hợp
Cho đồ thị hàm số ![]() như hình vẽ:
như hình vẽ:

Hỏi hàm số ![]() nghịch biến trên khoảng nào dưới đây?
nghịch biến trên khoảng nào dưới đây?
Theo đồ thị hàm số ta có hàm số đồng biến trên khoảng
và
khi đó:
Mặt khác
Do hàm số nghịch biến nên
Vậy hàm số nghịch biến trên khoảng
.
Chọn mệnh đề đúng
Cho hàm số ![]() có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau:

Mệnh đề nào sau đây đúng?
Tìm giá trị lớn nhất của hàm số
Giá trị lớn nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng
Ta có:
Suy ra hàm số nghịch biến trên đoạn .
Do đó
Khối lăng trụ ngũ giác
Khối lăng trụ ngũ giác có bao nhiêu cạnh?
Khối lăng trụ ngũ giác có số cạnh của một mặt đáy là 5 cạnh, số cạnh bên là 5 cạnh
Số cạnh của khối lăng trụ ngũ giác là: 2.5 + 5 =15 cạnh.
Chọn khẳng định đúng
Gọi ![]() lần lượt là số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
lần lượt là số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Tập xác định
Đồ thị hàm số không có tiệm cận ngang.
ta có
là tiệm cận đứng.
ta có:
là tiệm cận đứng.
Vậy .
Tìm số điểm cực trị của hàm số
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Số điểm cực trị của đồ thị hàm số là:
Dựa vào bảng biến thiên ta thấy hàm số có 3 điểm cực trị.
Chọn khẳng định đúng
Cho hàm số ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Tập xác định
Ghi đáp án vào ô trống
Có bao nhiêu giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên từng khoảng xác định?
đồng biến trên từng khoảng xác định?
Có bao nhiêu giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên từng khoảng xác định?
đồng biến trên từng khoảng xác định?
V lăng trụ đứng
Cho khối lăng trụ đứng ![]() có
có ![]() , đáy
, đáy ![]() là tam giác vuông cân tại
là tam giác vuông cân tại ![]() và
và ![]() . Tính thể tích của khối lăng trụ đã cho.
. Tính thể tích của khối lăng trụ đã cho.

Tam giác vuông cân tại
,
suy ra
Vậy thể tích khối lăng trụ
Tính giá trị biểu thức
Cho hàm số và có bảng biến thiên như hình vẽ.
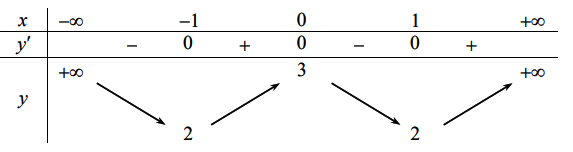
Tính ![]()
Ta có:
Chọn kết luận đúng
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số đã cho đồng biến trên khoảng và
.
Chọn đáp án đúng
Giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng
Ta có:
;
.
.
Giá trị của biểu thức M - 2m
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ![]() . Giá trị của biểu thức
. Giá trị của biểu thức ![]() là:
là:
Điều kiện xác định:
Xét hàm số trên
ta có:
Phương trình
Ta lại có:
=>
Xác định khoảng chứa các giá trị tham số m
Cho hàm số ![]() (với
(với ![]() là tham số) có đồ thị
là tham số) có đồ thị ![]() . Giả sử các điểm
. Giả sử các điểm ![]() là các điểm cực trị của
là các điểm cực trị của ![]() . Để tam giác
. Để tam giác ![]() đều thì giá trị của tham số
đều thì giá trị của tham số ![]() nằm trong khoảng nào sau đây?
nằm trong khoảng nào sau đây?
Tập xác định
Ta có:
Hàm số có ba điểm cực trị khi và chỉ khi phương trình có ba nghiệm phân biệt hay
có hai nghiệm khác 0
Khi đó
Đồ thị có ba điểm cực trị là
;
;
.
Ta có:
Do đó tam giác đều
Kết hợp với điều kiện .
Vậy đáp án cần tìm là .
Chọn đáp án đúng
Cho hàm số ![]() . Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
. Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
Tập xác định
Ta có:
Vậy đồ thị có một tiệm cận ngang .
Điền đáp án
Hình bát diện đều có tất cả bao nhiêu cạnh?
12 || mười hai || Mười hai
Hình bát diện đều có tất cả bao nhiêu cạnh?
12 || mười hai || Mười hai
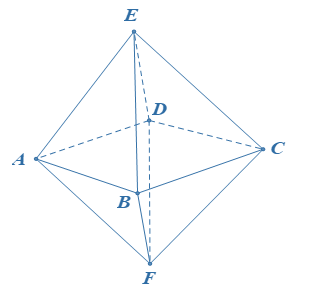
Hình bát diện đều có 12 cạnh.
Tìm m để hàm số đồng biến trên R
Tìm giá trị của tham số m để hàm số ![]() đồng biến trên
đồng biến trên ![]()
Ta có:
Hàm số đồng biến trên
Tính V biết khoảng cách
Cho khối chóp ![]() có đáy
có đáy ![]() là hình vuông cạnh
là hình vuông cạnh ![]() ,
, ![]() vuông góc với đáy và khoảng cách từ
vuông góc với đáy và khoảng cách từ ![]() đến mặt phẳng
đến mặt phẳng ![]() bằng
bằng ![]() . Tính thể tích
. Tính thể tích ![]() của khối chóp đã cho.
của khối chóp đã cho.

Gọi là hình chiếu của
trên
Ta có
Suy ra
Tam giác vuông tại
, có
Vậy .
Tính thể tích khối chóp
Cho khối chóp tứ giác đều ![]() có cạnh đáy bằng
có cạnh đáy bằng ![]() , góc giữa mặt bên và mặt đáy bằng
, góc giữa mặt bên và mặt đáy bằng ![]() . Thể tích
. Thể tích ![]() của khối chóp
của khối chóp ![]() bằng
bằng
Hình vẽ minh họa
Gọi là tâm của đáy, gọi
là trung điểm của
.
Ta có nên
Suy ra .
Có ,
.
Thể tích khối chóp là
.
Tìm điểm cực trị của hàm số
Biết rằng hàm số ![]() có một điểm cực trị
có một điểm cực trị ![]() . Tìm điểm cực trị còn lại
. Tìm điểm cực trị còn lại ![]() của hàm số.
của hàm số.
Ta có .
Để hàm số có hai điểm cực trị có hai nghiệm phân biệt
Theo giả thiết: (thỏa mãn
).
Với thì
Số cạnh của hình đa diện
Số cạnh của hình đa diện luôn luôn là một số tự nhiên
Có thể lấy tứ diện làm đại diện để xét với số đỉnh là 4, số cạnh là 6 và số mặt là 4.
Tìm số phần tử của tập S
Gọi S là tập hợp chứa tất cả các giá trị thực của tham số m để hàm số ![]() có điểm cực đại với giá trị cực đại tương ứng nằm trong khoảng (3; 4) và đồng thời thỏa mãn 10m là số nguyên. Số phần tử của tập hợp S là:
có điểm cực đại với giá trị cực đại tương ứng nằm trong khoảng (3; 4) và đồng thời thỏa mãn 10m là số nguyên. Số phần tử của tập hợp S là:
Xét phương trình
Nếu thì hàm số
không có điểm cực đại.
Nếu thì phương trình (*) có hai nghiệm phân biệt là
Với thì
không có điểm cực đại.
Với thì
Hàm số này đạt cực đại tại x = m + 2 và giá trị cực đại là
Vậy điều kiện để hàm số có cực đại là:
Do 10m là số nguyên nên có hai giá trị thỏa mãn là
Mp cách đều 4 đỉnh
Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?
Có 2 loại mặt phẳng thỏa mãn đề bài là:
a) Loại 1: Mặt phẳng qua trung điểm của 3 cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)

Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.
b) Loại 2: Mặt phẳng qua trung điểm của cạnh ( cạnh này thuộc cặp cạnh, mỗi cặp cạnh là chéo nhau). Có mặt phẳng như thế.

Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.
Ghi đáp án vào ô trống
Cho hàm số bậc ba ![]() có đồ thị như hình vẽ:
có đồ thị như hình vẽ:
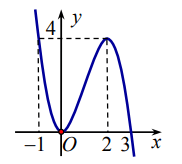
Có bao nhiêu giá trị của m để hàm số ![g\left( x ight) = \frac{{\left( {{x^2} - 2mx + {m^2} + m + 1} ight)\sqrt {{x^2} - 3x} }}{{\left( {x - 4} ight)\left[ {{f^2}\left( x ight) - 4f\left( x ight)} ight]}}](/data/image/holder.png) có 3 tiệm cận đứng?
có 3 tiệm cận đứng?
Cho hàm số bậc ba ![]() có đồ thị như hình vẽ:
có đồ thị như hình vẽ:

Có bao nhiêu giá trị của m để hàm số ![g\left( x ight) = \frac{{\left( {{x^2} - 2mx + {m^2} + m + 1} ight)\sqrt {{x^2} - 3x} }}{{\left( {x - 4} ight)\left[ {{f^2}\left( x ight) - 4f\left( x ight)} ight]}}](/data/image/holder.png) có 3 tiệm cận đứng?
có 3 tiệm cận đứng?
Tính V biết diện tích đáy
Tính thể tích ![]() của một khối lăng trụ biết đáy có diện tích
của một khối lăng trụ biết đáy có diện tích ![]() , cạnh bên tạo với mặt phẳng đáy một góc
, cạnh bên tạo với mặt phẳng đáy một góc ![]() và độ dài cạnh bên bằng 10 cm.
và độ dài cạnh bên bằng 10 cm.

Xét khối lăng trụ có đáy là tam giác ABC.
Gọi H là hình chiếu của A' trên mặt phẳng
.
Suy ra là hình chiếu của
trên mặt phẳng
.
Do đó
Tam giác vuông tại H, có
.
Vậy .
Tính theo a
Cho hình chóp ![]() có đáy ABC là tam giác vuông tại B và
có đáy ABC là tam giác vuông tại B và ![]() . Cạnh bên
. Cạnh bên ![]() và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp
và vuông góc với mặt phẳng đáy. Tính theo a thể tích V của khối chóp ![]() .
.

Diện tích tam giác vuông
Chiều cao khối chóp là .
Vậy thể tích khối chóp
Xét tính đúng sai của các nhận định
Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() và đồ thị như Hình 3.
và đồ thị như Hình 3.
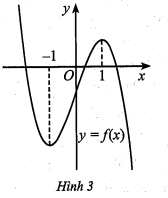
Các nhận định sau đúng hay sai?
a) Hàm số nghịch biến trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
b) Hàm số đạt cực tiểu tại điểm ![]() . Đúng||Sai
. Đúng||Sai
c) Đạo hàm của hàm số nhận giá trị không âm trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
d) Giá trị lớn nhất của hàm số trên đoạn ![]() bằng
bằng ![]() . Sai||Đúng
. Sai||Đúng
Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() và đồ thị như Hình 3.
và đồ thị như Hình 3.

Các nhận định sau đúng hay sai?
a) Hàm số nghịch biến trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
b) Hàm số đạt cực tiểu tại điểm ![]() . Đúng||Sai
. Đúng||Sai
c) Đạo hàm của hàm số nhận giá trị không âm trên khoảng ![]() . Đúng||Sai
. Đúng||Sai
d) Giá trị lớn nhất của hàm số trên đoạn ![]() bằng
bằng ![]() . Sai||Đúng
. Sai||Đúng
Theo Hình 3, hàm số nghịch biến trên khoảng và đạt cực tiểu tại điểm
.
Vì hàm số đồng biến trên khoảng nên đạo hàm của hàm số nhận giá trị không âm trên khoảng đó. Giá trị lớn nhất của hàm số trên đoạn
bằng
.
Đáp án: a) Đúng, b) Đúng, c) Đúng, d) Sai.
Tìm số mặt của đa diện
Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt ?
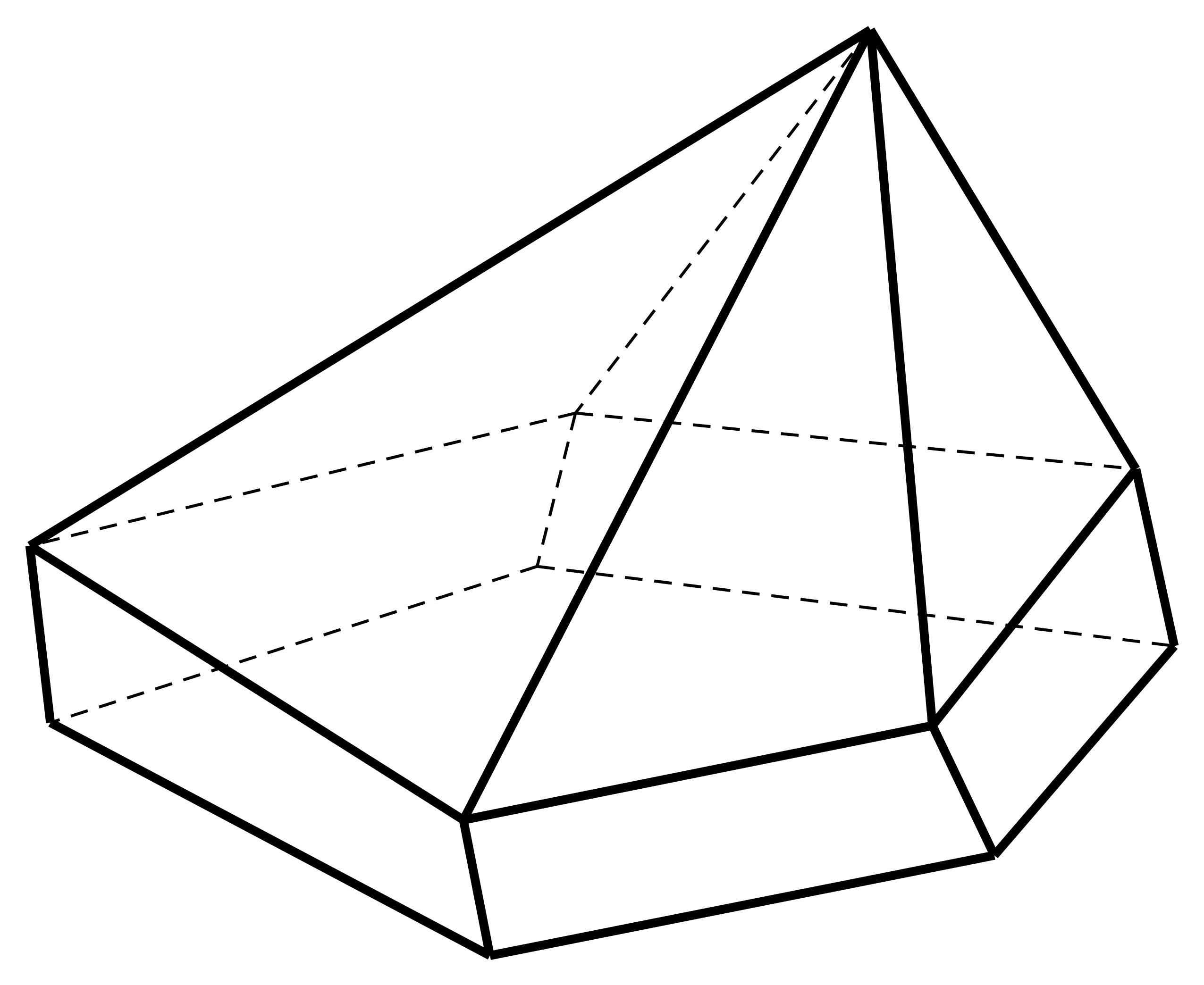
Quan sát hình vẽ và đếm các mặt xung quanh, chú ý cả những mặt được vẽ bằng nét đứt, không nhìn thấy được.
Chọn mệnh đề đúng
Cho hàm số ![]() với
với ![]() là tham số thực lớn hơn
là tham số thực lớn hơn ![]() thỏa mãn
thỏa mãn ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Ta có:
Do đó nghịch biến trên
.
Từ đó suy ra
Vậy đáp án đúng là .
Chọn phương án thích hợp
Cho hàm số ![]() có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là
có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục hoành là

Ta có tọa độ giao điểm của đồ thị hàm số và trục hoành là .
Chọn đáp án sai
Cho hàm số ![]() . Khẳng định nào sau đây sai?
. Khẳng định nào sau đây sai?
Ta có:
=> y = 2 là tiệm cận ngang của đồ thị hàm số
Ta cũng có: => x = 1; x = 32 là tiệm cận đứng của đồ thị hàm số
Ghi đáp án vào ô trống
Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() và có đồ thị như hình vẽ:
và có đồ thị như hình vẽ:

Xét hàm số ![]() . Tìm
. Tìm ![]() để
để ![]() .
.
Cho hàm số ![]() có đạo hàm trên
có đạo hàm trên ![]() và có đồ thị như hình vẽ:
và có đồ thị như hình vẽ:

Xét hàm số ![]() . Tìm
. Tìm ![]() để
để ![]() .
.
Tìm hình không phải đa diện
Cho các hình sau:
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:
Áp dụng định nghĩa hình đa diện, ta có:
“Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:
TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.
TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.
TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt sao cho S0 trùng với S, Sn trùng với S’ và bất kì hai mặt
nào
cũng đều có một cạnh chung.
Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”
Tìm số mặt của đa diện
Hình đa diện trong hình vẽ dưới đây có bao nhiêu mặt ?

Quan sát hình vẽ và đếm các mặt xung quanh, chú ý cả những mặt được vẽ bằng nét đứt, không nhìn thấy được.
Tìm m để hàm số có 3 cực trị
Cho hàm số ![]() với
với ![]() là tham số. Tìm các giá trị nguyên dương tham số
là tham số. Tìm các giá trị nguyên dương tham số ![]() không vượt quá
không vượt quá ![]() để hàm số đã cho có ba điểm cực trị?
để hàm số đã cho có ba điểm cực trị?
Hàm số có ba điểm cực trị khi và chỉ khi
.
Để hàm số đa cho có ba điểm cực trị khi và chỉ khi
Mà không vượt quá
nên
suy ra có
giá trị thỏa mãn yêu cầu.
Hình không phải đa diện lồi
Trong các hình dưới đây, hình nào không phải đa diện lồi?
Áp dụng dấu hiệu nhận biết của khối đa diện lồi : Đoạn thẳng nối hai điểm bất kì của
luôn thuộc
. Ta thấy có hình sau vi phạm tính chất đó:

Chọn đáp án đúng
Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:

Điểm cực đại của hàm số đã cho là
Từ BBT của hàm số suy ra điểm cực đại của hàm số
là
.
Tính tổng số cạnh
Tổng số cạnh của các loại hình {3;4} và {5;3} là bao nhiêu?
Hình {3;4} là khối bát diện đều, có 12 cạnh.
Hình {5;3} là khối mười hai mặt đều, có 30 cạnh.
Vậy tổng số cạnh của hai hình trên là cạnh.
Tìm tiệm cận ngang
Đường tiệm cận ngang của đồ thị hàm số ![]() có phương trình là:
có phương trình là:
Ta có:
Vậy đường thẳng là tiệm cận ngang của đồ thị hàm số.
Xác định tổng tất cả các giá trị của tham số m
Tính tổng ![]() tất cả các giá trị nguyên của tham số
tất cả các giá trị nguyên của tham số ![]() để hàm số
để hàm số ![]() đồng biến trên tập xác định?
đồng biến trên tập xác định?
Tập xác định
Ta có:
Để hàm số đồng biến trên tập xác định thì
Vì nên
Vậy .
Tìm hàm số đồng biến trên tập số thực
Cho hàm số sau, hàm số nào đồng biến trên ![]() ?
?
Xét hàm số ta có:
đồng biến trên
.
Chọn đáp án đúng
Cho hàm số ![]() có đạo hàm
có đạo hàm ![]() . Hàm số
. Hàm số ![]() đồng biến trên khoảng nào sau đây?
đồng biến trên khoảng nào sau đây?
Ta có bảng xét dấu:
Từ bảng xét dấu trên ta có hàm số đồng biến trên
.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
