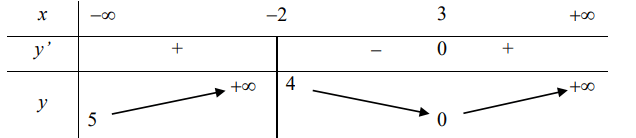
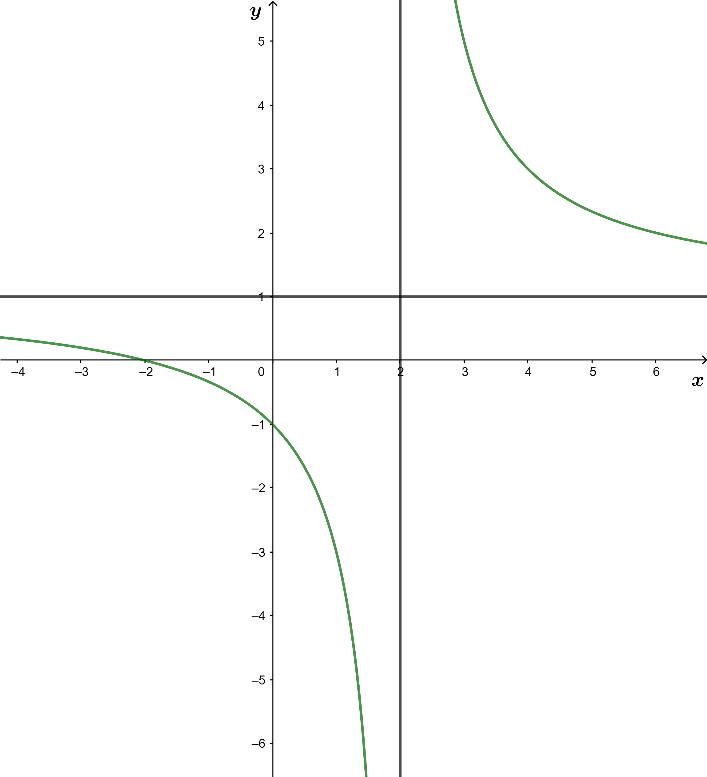Tìm điểm M thuộc đồ thị hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ điểm M đến trục hoành:
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Do M thuộc đồ thị hàm số nên tọa độ điểm
Phương trình tiệm cận đứng là x – 1 = 0 (d’)
Giải phương trình d(M,d’) = d(M, Ox)
=>