Tính tích phân lượng giác
Tích phân  có giá trị là:
có giá trị là:
Ta biến đổi:
Đặt
Đổi cận
Mời các bạn học cùng thử sức với Đề thi giữa HK2 môn Toán 12 nha!
Tính tích phân lượng giác
Tích phân  có giá trị là:
có giá trị là:
Ta biến đổi:
Đặt
Đổi cận
Xác định tọa độ điểm M
Trong không gian ![]() điểm
điểm ![]() thuộc trục
thuộc trục ![]() và cách đều hai điểm
và cách đều hai điểm ![]() và
và ![]() là
là
Ta có:
cách đều hai điểm
khi
Tìm kết luận sai
Trong các câu sau đây, nói về nguyên hàm của một hàm số ![]() xác định trên khoảng
xác định trên khoảng ![]() , câu nào là sai?
, câu nào là sai?
(I)![]() là nguyên hàm của
là nguyên hàm của ![]() trên
trên ![]() nếu và chỉ nếu
nếu và chỉ nếu ![]() .
.
(II) Nếu ![]() liên tục trên
liên tục trên ![]() thì
thì ![]() có nguyên hàm trên
có nguyên hàm trên ![]() .
.
(III) Hai nguyên hàm trên ![]() của cùng một hàm số thì sai khác nhau một hằng số.
của cùng một hàm số thì sai khác nhau một hằng số.
Không có đáp án nào sai.
Chọn đáp án đúng
Tìm nguyên hàm của hàm số ![]() .
.
Ta có
Chọn đáp án đúng
Hàm số ![]() là họ nguyên hàm của hàm số nào sau đây?
là họ nguyên hàm của hàm số nào sau đây?
Ta có: nên hàm số
là họ nguyên hàm của hàm số
.
Chọn đáp án đúng
Cho ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() . Tìm nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số ![]() .
.
Cách 1: Sử dụng tính chất của nguyên hàm .
Từ giả thiết, ta có
.
Suy ra .
Vậy .
Đặt .
.
Cách 2: Sử dụng công thức nguyên hàm từng phần.
Ta có
Từ giả thiết:
.
Vậy .
Thể tích của khối nón
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a, khoảng cách từ tâm O của đường tròn ngoại tiếp của đáy ABC đến một mặt bên là ![]() . Thể tích của khối nón ngoại tiếp hình chóp SABC bằng:
. Thể tích của khối nón ngoại tiếp hình chóp SABC bằng:

Gọi E là trung điểm của BC, dựng tại H.
Chứng minh được nên suy ra
.
Trong tam giác đều ABC, ta có
và
Trong tam giác vuông SOE, ta có
.
Vậy thể tích khối nón (đvtt).
Tìm mệnh đề sai
Cho hàm số ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() trên
trên ![]() . Các mệnh đề sau, mệnh đề nào sai.
. Các mệnh đề sau, mệnh đề nào sai.
Mệnh đề sai
Ghi đáp án vào ô trống
Cho hình lập phương ![]() có cạnh bằng
có cạnh bằng ![]() Gọi
Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() Tích vô hướng
Tích vô hướng ![]() (
(![]() là số thập phân). Giá trị của
là số thập phân). Giá trị của ![]() bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
Đáp án: -0,5||- 0,5
Cho hình lập phương ![]() có cạnh bằng
có cạnh bằng ![]() Gọi
Gọi ![]() lần lượt là trung điểm của
lần lượt là trung điểm của ![]() và
và ![]() Tích vô hướng
Tích vô hướng ![]() (
(![]() là số thập phân). Giá trị của
là số thập phân). Giá trị của ![]() bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
bằng bao nhiêu? (Kết quả ghi dưới dạng số thập phân)
Đáp án: -0,5||- 0,5
Hình vẽ minh họa
Vì nên
Ta có:
Vậy
Tìm phương trình mặt phẳng thích hợp
Trong không gian với hệ trục tọa độ ![]() , cho hai mặt phẳng có phương trình
, cho hai mặt phẳng có phương trình ![]() và mặt cầu
và mặt cầu ![]() . Mặt phẳng
. Mặt phẳng ![]() vuông với mặt phẳng
vuông với mặt phẳng ![]() đồng thời tiếp xúc với mặt cầu
đồng thời tiếp xúc với mặt cầu ![]() .
.
Mặt cầu có tâm
và bán kính
Gọi là một vectơ pháp tuyến của mặt phẳng
Ta có :
Lúc đó mặt phẳng có dạng :
.
Do mặt phẳng tiếp xúc với mặt cầu
Vậy phương trình mặt phẳng :
hoặc
.
Xác định diện tích hình phẳng S
Tính diện tích ![]() của hình phẳng giới hạn bởi đồ thị hàm số
của hình phẳng giới hạn bởi đồ thị hàm số ![]() , trục hoành
, trục hoành ![]() , các đường thẳng
, các đường thẳng ![]() ,
, ![]() .
.
Diện tích hình phẳng là
.
Chọn mệnh đề đúng
Cho hàm số ![]() thỏa mãn
thỏa mãn ![]() và
và ![]() . Mệnh đề nào dưới đây đúng?
. Mệnh đề nào dưới đây đúng?
Ta có
Do nên
.
Vậy .
Tính thời gian đi đến trường
Một học sinh đi học từ nhà đến trường bằng xe đạp với vận tốc thay đổi theo thời gian được tính bởi công thức ![]() . Biết rằng sau khi đi được 1 phút thì quãng đường học sinh đó đi được là
. Biết rằng sau khi đi được 1 phút thì quãng đường học sinh đó đi được là ![]() . Biết quãng đường từ nhà đến trường là
. Biết quãng đường từ nhà đến trường là ![]() . Hỏi thời gian học sinh đó đi đến trường là bao nhiêu phút?
. Hỏi thời gian học sinh đó đi đến trường là bao nhiêu phút?
Ta có:
Vì
Để học sinh đó đến trường thì
Vậy đáp án cần tìm là phút.
Xác định tính đúng sai của từng phương án
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Các khẳng định sau là đúng hay sai?
. Các khẳng định sau là đúng hay sai?
a) Tọa độ điểm A là ![]() . Đúng||Sai
. Đúng||Sai
b) Hình chiếu vuông góc của ![]() lên trục
lên trục ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
c) Trung điểm của ![]() là
là ![]() . Đúng||Sai
. Đúng||Sai
d) Hình chiếu vuông góc của ![]() lên mặt phẳng
lên mặt phẳng ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
Trong không gian ![]() , cho vectơ
, cho vectơ ![]() . Các khẳng định sau là đúng hay sai?
. Các khẳng định sau là đúng hay sai?
a) Tọa độ điểm A là ![]() . Đúng||Sai
. Đúng||Sai
b) Hình chiếu vuông góc của ![]() lên trục
lên trục ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
c) Trung điểm của ![]() là
là ![]() . Đúng||Sai
. Đúng||Sai
d) Hình chiếu vuông góc của ![]() lên mặt phẳng
lên mặt phẳng ![]() là
là ![]() . Sai||Đúng
. Sai||Đúng
a) Ta có
b) Hình chiếu vuông góc của A lên Ox là .
c) Trung điểm của là điểm
.
d) Hình chiếu vuông góc của lên mặt phẳng
là
.
Chọn phương án đúng
Tìm nguyên hàm ![]()
Ta có
Áp dụng vào bài ta chọn .
Chọn mệnh đề đúng
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
Vì tọa độ điểm có
nên
.
Tìm tích phân
Biết ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
Ta có:
Chọn mệnh đề đúng
Cho hàm số ![]() liên tục nhận giá trị dương trên
liên tục nhận giá trị dương trên ![]() và thỏa mãn
và thỏa mãn ![]() ;
; ![]() . Giá trị
. Giá trị ![]() gần nhất với giá trị nào sau đây?
gần nhất với giá trị nào sau đây?
Vì
Mà
Tính khoảng cách
Cho hình chóp ![]() có đường thẳng
có đường thẳng ![]() vuông góc với đáy
vuông góc với đáy ![]() ,
, ![]() . Khoảng cách từ điểm
. Khoảng cách từ điểm ![]() đến đường thẳng
đến đường thẳng ![]() bằng:
bằng:
Vì vuông góc với đáy
nên
Tính tích phân I
Giả sử ![]() và
và ![]() . Tính
. Tính ![]()
Ta có:
Xác định mệnh đề sai
Cho hàm số ![]() . Gọi
. Gọi ![]() là diện tích hình phẳng giới hạn bởi đồ thị hàm số
là diện tích hình phẳng giới hạn bởi đồ thị hàm số ![]() và trục hoành. Mệnh đề nào sau đây sai?
và trục hoành. Mệnh đề nào sau đây sai?
Phương trình hoành độ giao điểm:
Diện tích hình phẳng cần tìm là:
((do trong khoảng (0; 1) và (1; 2) phương trình
vô nghiệm)
Vậy mệnh đề sai là: .
Tính góc giữa hai mặt phẳng
Cho hình vuông ![]() có cạnh
có cạnh ![]() . Trên hai tia
. Trên hai tia ![]() vuông góc và nằm cùng phía với mặt phẳng
vuông góc và nằm cùng phía với mặt phẳng ![]() lần lượt lấy hai điểm
lần lượt lấy hai điểm ![]() sao cho
sao cho ![]() . Tính góc
. Tính góc ![]() giữa hai mặt phẳng
giữa hai mặt phẳng ![]() .
.
Hình vẽ minh họa
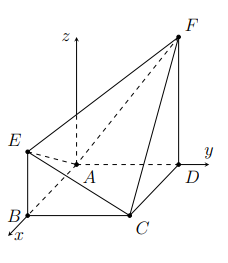
Đặt hình vẽ vào hệ trục tọa độ sao cho
trùng với O(0; 0; 0), B thuộc Ox và có tọa độ B(a; 0; 0), D thuộc Oy và có thọa độ D(0; a; 0).
Khi đó ta được .
(AEF) có một vectơ pháp tuyến là
=> cũng là vectơ pháp tuyến của (CEF)
(CEF) có một vtơ pháp tuyến là:
cũng là vectơ pháp tuyến của (CEF).
.
Chọn phương án đúng
Tìm nguyên hàm ![]()
Ta có
Áp dụng vào bài ta chọn .
Tìm giá trị của I
Cho tích phân ![]() . Biết rằng
. Biết rằng ![]() là nguyên hàm của
là nguyên hàm của ![]() . Giá trị của I là:
. Giá trị của I là:
Cho tích phân . Biết rằng
là nguyên hàm của
. Giá trị của I là:
Ta có ngay kết quả .
Đáp án đúng là .
Tính khoảng cách
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng ![]() . Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng
. Hai điểm A, B lần lượt nằm trên hai đường tròn đáy sao cho góc giữa AB và trục của hình trụ bằng ![]() . Khoảng cách giữa AB và trục của hình trụ bằng:
. Khoảng cách giữa AB và trục của hình trụ bằng:

Từ hình vẽ kết hợp với giả thiết, ta có .
Gọi AA’ là đường sinh của hình trụ thì và
.
Vì nên
Gọi H là trung điểm A’B, suy ra
nên .
Tam giác ABA’ vuông tại A’ nên
Suy ra tam giác A’BO đều có cạnh bằng R nên
Chọn công thức tính diện tích hình phẳng
Cho đồ thị hàm số ![]() như hình vẽ:
như hình vẽ:

Diện tích ![]() của hình phẳng được giới hạn bởi đồ thị hàm số
của hình phẳng được giới hạn bởi đồ thị hàm số ![]() và trục
và trục ![]() (phần gạch sọc) được tính bởi công thức
(phần gạch sọc) được tính bởi công thức
Từ đồ thị hàm số ta thấy
Do đó:
Tìm nguyên hàm của hàm số
Nguyên hàm của hàm số ![]() bằng
bằng
Ta có:
Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3
Một chất điểm dạng chuyển động với vận tốc ![]() thì tăng tốc với gia tốc
thì tăng tốc với gia tốc ![]() . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3s kể từ lúc bắt đầu tăng tốc.
. Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3s kể từ lúc bắt đầu tăng tốc.
Ta có:
Do khi bắt đầu tăng tốc nên
Khi đó quãng đường xe đi được sau 3 giây kể từ khi ô tô tăng tốc bằng:
Xác định vectơ pháp tuyến của mặt phẳng
Trong không gian với hệ trục tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
Mặt phẳng có một vectơ pháp tuyến là
.
Độ dài đường sinh
Cho mặt cầu tâm O, bán kính R = a. Một hình nón có đỉnh S là ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng SO tại H sao cho ![]() . Độ dài đường sinh
. Độ dài đường sinh ![]() của hình nón bằng:
của hình nón bằng:

Gọi S' là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.
Tam giác SAS’ vuông tại A và có đường cao AH nên
Thể tích của khối trụ
Cho hình trụ có chiều cao bằng 8a . Biết hai điểm A và C lần lượt nằm trên hai đáy thỏa mãn ![]() , khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:
, khoảng cách giữa AC và trục của hình trụ bằng 4a. Thể tích của khối trụ đã cho là:

Gọi (O) và (O') lần lượt là hai đường tròn đáy; .
Dựng AD, CB lần lượt song song với OO' . Dễ dàng có ABCD là hình chữ nhật.
Do .
Gọi H là trung điểm của DC.
.
Ta có .
Suy ra .
Vậy thể tích của khối trụ là .
Tìm nguyên hàm của hàm số
Xác định nguyên hàm ![]() của hàm số
của hàm số ![]() ?
?
Ta có:
Ghi đáp án vào ô trống
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() là mặt phẳng thay đổi qua
là mặt phẳng thay đổi qua ![]() và cắt các trục
và cắt các trục ![]() lần lượt tại
lần lượt tại ![]() với
với ![]() . Khi diện tích tam giác
. Khi diện tích tam giác ![]() nhỏ nhất, hãy tính giá trị của tích
nhỏ nhất, hãy tính giá trị của tích ![]() ?
?
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Gọi
. Gọi ![]() là mặt phẳng thay đổi qua
là mặt phẳng thay đổi qua ![]() và cắt các trục
và cắt các trục ![]() lần lượt tại
lần lượt tại ![]() với
với ![]() . Khi diện tích tam giác
. Khi diện tích tam giác ![]() nhỏ nhất, hãy tính giá trị của tích
nhỏ nhất, hãy tính giá trị của tích ![]() ?
?
Tính khoảng cách d(M; (P))
Trong không gian với hệ tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() và điểm
và điểm ![]() . Tính khoảng cách
. Tính khoảng cách ![]() từ
từ ![]() đến
đến ![]() .
.
Khoảng cách từ M đến mặt phẳng (P) là:
Tính giá trị biểu thức
Biết rằng ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có:
Khi đó
Suy ra
Mệnh đề đúng
Xét các mệnh đề:
(I) Tập hợp các đường thẳng d thay đổi nhưng luôn luôn song song và cách đường thẳng ![]() cố định một khoảng không đổi là một mặt trụ.
cố định một khoảng không đổi là một mặt trụ.
(II) Hai điểm A, B cố định. Tập hợp các điểm M trong không gian mà diện tích tam giác MAB không đổi là một mặt trụ.
Trong các mệnh đề trên, mệnh đề nào đúng?
Ta xét về khái niệm Mặt trụ suy ra (I) đúng.
Diện tích tam giác MAB không đổi khi và chỉ khi khoảng cách từ M đến đường thẳng AB không đổi (giả sử bằng R ).
Vậy tập hợp các điểm M là mặt trụ bán kính R và trục là AB.
Vì vậy Mệnh đề (II) cũng đúng.
Tìm nguyên hàm của hàm số f(x) = 7^x
Tìm nguyên hàm của hàm số ![]() là
là
Ta có:
Tìm phương trình mặt phẳng
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() , đồng thời vuông góc với giá của vectơ
, đồng thời vuông góc với giá của vectơ ![]() có phương trình là:
có phương trình là:
Mặt phẳng nhận vectơ
làm vectơ pháp tuyến và đi qua điểm
nên có phương trình là
.
Tính giá trị biểu thức
Cho hàm số ![]() là một nguyên hàm của
là một nguyên hàm của ![]() , biết rằng
, biết rằng ![]() . Khi đó giá trị
. Khi đó giá trị ![]() là:
là:
Ta có:
Mà . Vậy với
thì
Vậy .
PT mp chứa giao tuyến
Cho hai mặt phẳng ![]() và
và ![]() . Với
. Với ![]() cho biết
cho biết ![]() và cặp vectơ chỉ phương
và cặp vectơ chỉ phương ![]() . Với
. Với ![]() cho PTTQ
cho PTTQ ![]() . Phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của
. Phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của ![]() và
và ![]() , qua điểm
, qua điểm ![]() là:
là:
Trước tiên, ta cần đưa phương trình về dạng tổng quát.
Theo đề bài, ta có và cặp vectơ chỉ phương
nên vecto pháp tuyến của mp
là tích có hướng của 2 vecto chỉ phương.
Ta có .
Chọn làm vectơ pháp tuyến cho
thì phương trình tổng quát của
có dạng
.
Vậy phương trình
Để tìm phương trình tổng quát của mặt phẳng (P) chứa giao tuyến của và
ta xét chùm mặt phẳng :
Mặt khác, ta có
Thế vào (*) ta được:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
