Cho hàm số có bảng biến như sau:
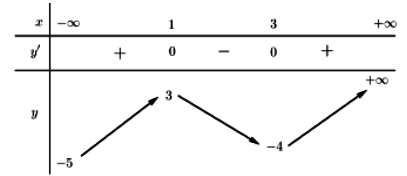
Tìm tất cả các giá trị của tham số m để bất phương trình có một nghiệm?
Đặt
Khi đó bất phương trình trở thành
Bất phương trình có nghiệm khi bất phương trình
có nghiệm
Hãy cùng thử sức kiểm tra đánh giá các kiến thức tổng quan với bộ đề Trắc nghiệm Ôn tập chương 1: Ứng dụng đạo hàm khảo sát và vẽ đồ thị các em nhé!
Cho hàm số có bảng biến như sau:

Tìm tất cả các giá trị của tham số m để bất phương trình có một nghiệm?
Đặt
Khi đó bất phương trình trở thành
Bất phương trình có nghiệm khi bất phương trình
có nghiệm
Cho hàm số có đạo hàm
liên tục trên
và có bảng biến thiên như sau:
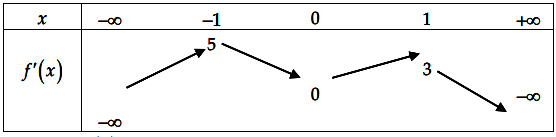
Bất phương trình (m là tham số thực) nghiệm đúng với
khi và chỉ khi
Ta có:
Xét hàm số với
Ta có:
=> Hàm số g(x) luôn đồng biến trên
Ta có bảng biến thiên như sau:

=> (*) nghiệm đúng khi
Hàm số nào sau đây đồng biến trên ?
Hàm số có
Cho hàm số
Ta có: có hai nghiệm phân biệt là -2 và 3
=> f’(x) < 0 =>
Vậy hàm số nghịch biến trên khoảng (-2; 3)
Tìm giá trị thực của tham số m để hàm số f(x) = -x3 – 3x2 + m có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.
Xét hàm số f(x) = -x3 – 3x2 + m trên đoạn [-1; 1] ta có:
f’(x) = -3x2 – 6x
f’(x) = 0 =>
Ta tính được
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là:
Tập xác định
Ta có:
Hàm số có bao nhiêu điểm cực trị?
Tập xác định
Ta có:
Do y’ không đổi dấu nên hàm số không có cực trị.
Gọi A, B, C là các điểm cực trị của đồ thị hàm số . Bán kính của đường tròn nội tiếp tam giác ABC bằng:
Ta có:
=> Đồ thị hàm số có ba điểm cực trị là A(0; 4), B(1; 3), C(-1;; 3)
Tính được
Áp dụng công thức tính bán kính đường tròn nội tiếp tam giác ABC ta có:
Cho hàm số . Trong các khẳng định sau, khẳng định nào là khẳng định đúng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Điều kiện
Từ điều kiện ta có:
Đồ thị hàm số không có tiệm cận đứng
Mặt khác
=> y = 0 là tiệm cận ngang của đồ thị hàm số
Không tồn tại
Vậy đồ thị hàm số không có tiệm cận đứng và có đúng một tiệm cận ngang
Giá trị nhỏ nhất của hàm số y = x3 – 3x + 5 trên đoạn [0; 2] là:
Xét hàm số f(x) = x3 – 3x + 5 trên [0; 2] có:
f’(x) = 3x3 – 3
f’(x) = 0 =>
Tính được f(0) = 5; f(1) = 3; f(2) = 7
Vậy
Giá trị nhỏ nhất của hàm số là:
Tập xác định
Biến đổi f(x) như sau:
Đặt
Hàm số đã cho trở thành
Vậy giá trị nhỏ nhất của hàm số đã cho bằng 2018 tại
Cho hàm số f(x) có bảng xét dấu đạo hàm f’(x) như sau:

Hàm số f(x) có bao nhiêu điểm cực đại?
Dựa vào bảng xét dấu đạo hàm f’(x) ta thấy đạo hàm f’(x) đổi dấu từ dương sang âm 2 lần nên f(x) có 2 điểm cực đại.
Cho hàm số có bảng biến như sau:

Tìm tất cả các giá trị của tham số m để bất phương trình có một nghiệm?
Đặt
Khi đó bất phương trình trở thành
Bất phương trình có nghiệm khi bất phương trình
có nghiệm
Cho hàm số bậc bốn có đồ thị như hình vẽ dưới đây:

Số điểm cực trị của hàm số là:
Ta có:
Cho hàm số | 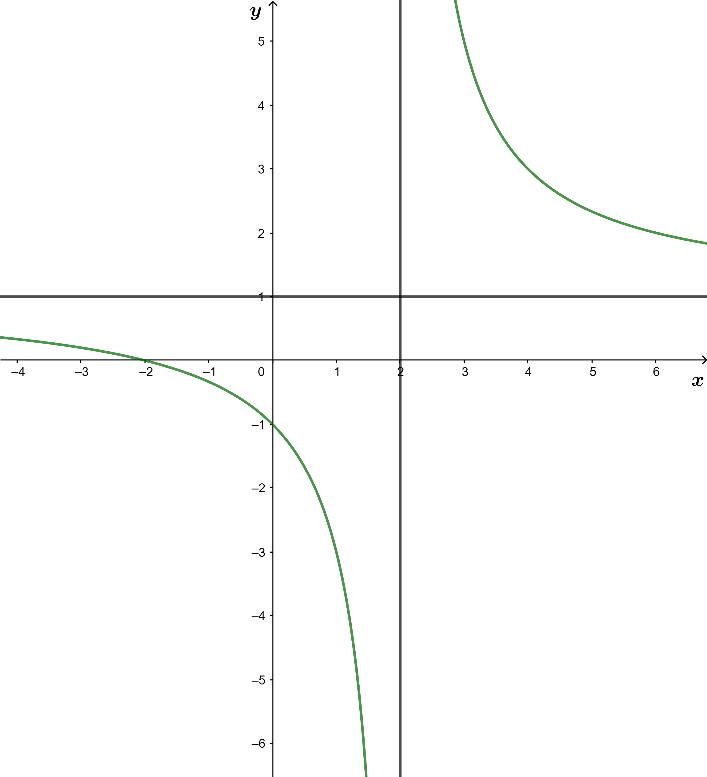 |
Dựa vào đồ thị hàm số để xác định nghiệm của mẫu số và tử số từ đó suy ra các đường tiệm cận đứng của đồ thị hàm số.
Tìm các giới hạn để tìm các đường tiệm cận ngang của đồ thị hàm số.
Từ đồ thị hàm số ta có nhận xét như sau:
Đường thẳng x = 2 là tiệm cận đứng của đồ thị (C)
=>
Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số (C)
=>
Điểm có tọa độ (0; -1) thuộc đồ thị hàm số (C)
=> y(0) = -1 =>
=>
Cho hàm số (với m là tham số thực). Tìm giá trị lớn nhất của tham số m để hàm số có giá trị nhỏ nhất bằng -2 trên đoạn [0; 3].
Xét hàm số trên đoạn [0; 3] ta có:
=> Hàm số f(x) đồng biến trên (0; 3)
=>
Theo bài ra ta có:
Hàm số đồng biến trên khoảng
Ta có y’ = 8x => y’ = 0 => x = 0
=> y’ > 0 => x > 0
=> y’ < 0 => x < 0
Vậy hàm số đồng biến trên khoảng
Độ giảm huyết áp của một bệnh nhân được cho bởi công thức , trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.
Xét ta có:
Mặt khác
Cho hàm số y = f(x) như hình vẽ. Hỏi có tất cả bao nhiêu giá trị thực của tham số m để hàm số có đúng 6 điểm cực trị?
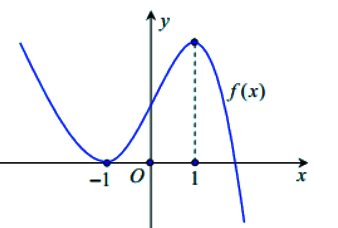
Xét hàm số
Yêu cầu bài toán xảy ra khi phương trình đạo hàm phải có 6 nghiệm bội lẻ:
Ta có:
Phương trình (*) luôn có hai nghiệm phân biệt => Hai phương trình còn lại phải cho đúng 4 nghiệm nghiệm bội lẻ.
Nhận thấy hai phương trình (1), (2) luôn cho hai nghiệm phân biệt vafcacs nghiệm của hai phương trình này không trùng nhau.
Để hai phương trình có đúng 4 nghiệm bội lẻ thì:
TH1: x = 1 là nghiệm của (x – 1)[x2 – (m – 1)x – m – 1] = 0 và x = -1 không phải là nghiệm của (x – 1)[x2 – (m + 1)x + m – 1] = 0
TH2: x = -1 là nghiệm của (x – 1)[x2 – (m + 1)x + m – 1] = 0 và x = 1 không phải là nghiệm của (x – 1)[x2 – (m – 1)x - m – 1] = 0
=>
Vậy có hai giá thực của m thỏa mãn
Cho hàm số có bảng biến thiên như hình vẽ. Hỏi hàm số đã cho là hàm số nào?
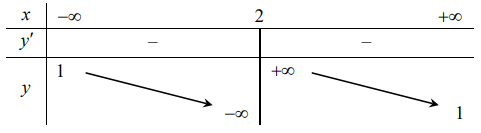
Dựa vào bảng biến thiên ta thấy:
Đồ thị hàm số nhận các đường thẳng x = 2 và tiệm cận ngang y = 1
=> Loại đáp án C và D
Hàm số đã cho nghịch biến trên mỗi khoảng xác định
Xét hàm số
=> Hàm số đồng biến trên mỗi khoảng xác định nên ta loại đáp án A
Cho hàm số y = f(x) có đạo hàm . Hỏi hàm số có bao nhiêu điểm cực trị?
Ta có:
=> Hàm số có 1 cực trị
Gọi K là tập hợp các giá trị nguyên của tham số để bất phương trình
nghiệm đúng với mọi
. Số các phần tử của tập hợp K là:
Đặt
Bất phương trình đã cho trở thành
Yêu cầu bài toán tương đương với bất phương trình (*) nghiệm đúng với mọi
Xét hàm số
Vì
Do đó bất phương trình (*) nghiệm đúng với mọi khi và chỉ khi
Mặt khác m là số nguyên thuộc [0; 2019] nên
Cho hàm số y = f(x) có đạo hàm trên là
. Hàm số đã cho có bao nhiêu điểm cực trị?
Tập xác định:
Ta có:
Ta có bảng xét dầu’(x) như sau:

Dựa vào bảng xét dấy của f’(x) ta thấy f’(x) đổi dấu qua hai điểm x = 2018, x = 2019 nên hàm số đã cho có hai điểm cực trị.
Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số ?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Xét phương trình x + 1 = 0 => x = -1
Và => x = -1 là tiệm cận đứng của đồ thị hàm số.
Cho hàm số y = f(x) là hàm số bậc 2. Đồ thị hàm số y = f’(x) như hình vẽ dưới đây và f(-1) < 20
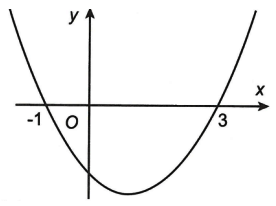
Đồ thị hàm số (m là tham số thực) có bốn tiệm cận khi và chỉ khi:
Điều kiện
Từ đồ thị hàm số f’(x) ta có bảng biến thiên hàm số f(x) là:

Nếu m = 20 thì đồ thị hàm số không có đủ bốn tiệm cận
Nếu thì
=> y = 1 là tiệm cận ngang của đồ thị hàm số
Ta có phương trình f(x) = 20 có một nghiệm x = a > 3 vì f(-1) < 20
=> Đồ thị hàm số g(x) có bốn tiệm cận khi phương trình f(x) = m có ba nghiệm phân biệt khác a
=> f(3) < m < f(-1)
Cho hàm số . Khẳng định nào sau đây sai?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có tiệm cận đứng của hàm số là y = 3 và tiệm cận ngang là y = 1
Giao điểm của hai đường tiệm cận I(3; 1) là tâm đối xứng của đồ thị
=> A, C, D đúng và B sai
Cho hàm số . Số nghiệm thực phân biệt của phương trình
là:
Ta có:
Đồ thị của hàm số được minh họa bằng hình vẽ sau:

Từ đồ thị ta suy ra
Phương trình (*) có 3 nghiệm thực
Phương trình (**) có 2 nghiệm thực
Một tạp chí bán được 25 000 đồng một cuốn. Chi phía xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, …) được cho bởi công thức , C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 6 000 đồng. Các khoản thu khi bán tạp chí bao gồm tiền bán tạp chí và 100 triệu đồng nhận được từ quảng cá. Giả sử số cuốn in ra đều được bán hết. Tính số tiền lãi lớn nhất có thể có khi bán tạp chí.
Một tạp chí bán được 25 000 đồng một cuốn. Chi phía xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, …) được cho bởi công thức , C(x) được tính theo đơn vị vạn đồng. Chi phí phát hành cho mỗi cuốn là 6 000 đồng. Các khoản thu khi bán tạp chí bao gồm tiền bán tạp chí và 100 triệu đồng nhận được từ quảng cá. Giả sử số cuốn in ra đều được bán hết. Tính số tiền lãi lớn nhất có thể có khi bán tạp chí.
Cho hàm số y = f(x) có và
. Khẳng định nào sau đây là khẳng định đúng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Ta có: => Đồ thị hàm số đã cho có TCĐ là x = 0
=> Đồ thị hàm số đã cho có TCĐ là x = 2
Cho hàm số liên tục trên
và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị của tham số m để phương trình
có bốn nghiệm thuộc đoạn
là:
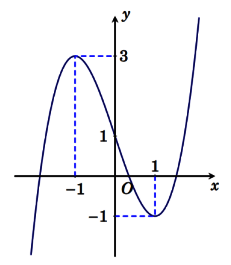
Đặt
Ta có:
Ta có đồ thị hình vẽ như sau:

Dựa vào đồ thị hàm số, phương trình đã cho có 4 nghiệm thuộc đoạn khi phương trình (*) có hai nghiệm
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
