Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Khóa học Lớp 12 Toán 12 (cũ)
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Đề thi học kì 1 Toán 12 Đề 2

Mô tả thêm:

Mời các bạn học cùng thử sức với Đề thi học kì 1 môn Toán lớp 12 nha!
  • Thời gian làm: 90 phút
  • Số câu hỏi: 50 câu
  • Số điểm tối đa: 50 điểm
Trước khi làm bài bạn hãy
  • 1 Ôn tập kiến thức đã nêu trong phần Mô tả thêm
  • 2 Tìm không gian và thiết bị phù hợp để tập trung làm bài
  • 3 Chuẩn bị sẵn dụng cụ cần dùng khi làm bài như bút, nháp, máy tính
  • 4 Căn chỉnh thời gian làm từng câu một cách hợp lý
Bắt đầu làm bài
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
  • Câu 1: Vận dụng

    Tổng độ dài

    Tổng độ dài \ell của tất cả các cạnh của khối mười hai mặt đều cạnh bằng 2

    60 || sáu mươi || Sáu mươi

    Đáp án là:

    Tổng độ dài \ell của tất cả các cạnh của khối mười hai mặt đều cạnh bằng 2

    60 || sáu mươi || Sáu mươi

     Khối mười hai mặt đều có tất cả 30 cạnh:

     Suy ra ta có tổng độ dài tất cả các cạnh bằng \ell = 30.2 = 60.

  • Câu 2: Vận dụng

    Khẳng định nào sau đây là đúng?

    Cho biểu thức P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} với a và b là các số thực dương. Khẳng định nào sau đây là đúng?

     Thực hiện thu gọn biểu thức như sau:

    \begin{matrix} P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.{{\left( {{a^2}{b^2}} ight)}^{\frac{2}{3}}}} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{{ - 1}}{2}}}.{b^{\frac{{ - 1}}{3}}}.\left( {{a^{\frac{4}{3}}}{b^{\frac{4}{3}}}} ight)} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{{\left[ {{a^{\frac{5}{6}}}.b} ight]}^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{1}{3}}}.{a^{\frac{{ - 5}}{{12}}}}.{b^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {\left\{ {{a^{\frac{{ - 1}}{{12}}}}.{b^{\frac{{ - 1}}{2}}}} ight\}^6} \hfill \\ P = {a^{\frac{{ - 1}}{2}}}.{b^{ - 3}} = \dfrac{1}{{{b^3}\sqrt a }} = \dfrac{{\sqrt a }}{{a{b^3}}} \hfill \\ \end{matrix}

  • Câu 3: Vận dụng cao

    Ghi đáp án vào ô trống

    Cho hàm số f(x) mà đồ thị hàm số y = f’(x) được biểu diễn như hình vẽ:

    Bất phương trình nghiệm đúng với mọi x thuộc khoảng

    Giả sử bất phương trình f\left( x ight) > \sin \frac{{\pi x}}{2} + m nghiệm đúng với mọi x \in \left[ { - 1;3} ight] thì tham số m thỏa mãn điều kiện là:

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số f(x) mà đồ thị hàm số y = f’(x) được biểu diễn như hình vẽ:

    Bất phương trình nghiệm đúng với mọi x thuộc khoảng

    Giả sử bất phương trình f\left( x ight) > \sin \frac{{\pi x}}{2} + m nghiệm đúng với mọi x \in \left[ { - 1;3} ight] thì tham số m thỏa mãn điều kiện là:

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 4: Nhận biết

    Chọn đáp án đúng

    Chọn hàm số có nhiều điểm cực trị nhất trong các hàm số sau?

    Ta có:

    Hàm số y = - 3x + 1 và y = \frac{2x + 1}{x - 3} không có điểm cực trị (đạo hàm không đổi dấu).

    Hàm số y = x^{4} + 3x^{2} + 1 có y' = 4x^{3} + 6x = 0 \Leftrightarrow x = 0. Đạo hàm đổi dấu qua 1 điểm x = 0 nên hàm số y = x^{4} + 3x^{2} + 1 chỉ có một điểm cực trị.

    Hàm số y = x^{3} - 3x^{2} + 1 có y' = 3x^{2} - 6x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.. Đạo hàm đổi dấu qua hai điểm x = 0 và x = 2 nên hàm số y = x^{3} - 3x^{2} + 1 có hai điểm cực trị.

    Vậy hàm số có nhiều điểm cực trị nhất là: y = x^{3} - 3x^{2} + 1.

  • Câu 5: Thông hiểu

    Trong các khẳng định sau khẳng định nào đúng?

    Cho một số thực \alpha tùy ý. Trong các khẳng định sau khẳng định nào đúng?

     Theo tính chất đạo hàm của hàm số lũy thừa, hàm số y = {x^\alpha } có đạo hàm với mọi x > 0 và \left( {{x^\alpha }} ight)' = \alpha {x^{\alpha - 1}}

  • Câu 6: Nhận biết

    Đạo hàm của hàm số lũy thừa

    Đạo hàm của hàm số y = \frac{{{e^{4x}}}}{5}

    Ta có: y' = \frac{1}{5}\left( {{e^{4x}}} ight)' = \frac{1}{5}\left( {4x} ight)'.{e^{4x}} = \frac{4}{5}.{e^{4x}}

  • Câu 7: Nhận biết

    Xác định đường kính mặt cầu

    Đường kính của mặt cầu (S):x^{2} + y^{2} + (z - 1)^{2} = 4 bằng:

    Mặt cầu (S) có bán kính R = 2 suy ra đường kính có độ dài: 2R = 4.

    Đường kính của mặt cầu (S):x^{2} + y^{2} + (z - 1)^{2} = 4 bằng: 4.

  • Câu 8: Vận dụng

    Chọn phương án đúng

    Tìm tập các tâm I của mặt cầu (S) tiếp xúc với hai mặt phẳng (P): x - 2y + 2z + 4 = 0;(Q):x - 2y + 2z - 6 = 0.

    Gọi A( - 4,0,0) và B(6, 0 , 0) lần lượt là giao điểm của trục x’Ox với (P) và (Q). Trung điểm E(1,0,0) của AB cách đều (P) và (Q).

    Tâm I cách đều (P) và (Q)

    \Rightarrow EI nằm trong mặt (R) qua E song song và cách đều (P) và (Q) ((P)//(Q)).

    \Rightarrow (R):x - 2y + 2z + D = 0,E \in (R) \Rightarrow D = - 1

    Vậy I \in (R):x - 2y + 2z - 1 = 0

  • Câu 9: Thông hiểu

    Tính V lăng trụ

    Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B và BA=BC=1. Cạnh A'B tạo với mặt đáy (ABC) góc 60^0. Tính thể tích V của khối lăng trụ đã cho.

     

    Vì ABC.A'B'C' là lăng trụ đứng nên AA' \bot \left( {ABC} ight), suy ra hình chiếu vuông góc của A'B trên mặt đáy (ABC) là AB.

    Do đó {60^0} = \widehat {A'B,\left( {ABC} ight)} = \widehat {A'B,AB} = \widehat {A'BA}.

    Tam giác vuông A'AB, ta có AA' = AB.\tan \widehat {A'BA} = \sqrt 3

    Diện tích tam giác là {S_{\Delta ABC}} = \frac{1}{2}BA.BC = \frac{1}{2}

    Vậy V = {S_{\Delta ABC}}.AA' = \frac{{\sqrt 3 }}{2}.

  • Câu 10: Thông hiểu

    Chọn mệnh đề đúng

    Biết rằng giá trị nhỏ nhất của hàm số f(x) = \frac{mx + 5}{x - m} trên đoạn \lbrack 0;1brack bằng - 7. mệnh đề nào sau đây đúng?

    Ta có: y' = - \frac{m^{2} + 5}{(x -m)^{2}} < 0;\forall x eq m \Rightarrow \Delta' = m^{2} + 2m -3

    Suy ra hàm số luôn nghịch biến trên các khoảng ( - \infty;m) và (m; + \infty)

    Vì hàm số có giá trị nhỏ nhất trên đoạn \lbrack 0;1brack nên m otin \lbrack 0;1brack

    Hàm số có giá trị nhỏ nhất trên đoạn \lbrack 0;1brack bằng - 7 nên suy ra

    \left[ \begin{gathered} \left\{ \begin{gathered} m > 1 \hfill \\ f\left( 1 ight) = \frac{{m + 5}}{{1 - m}} = - 7 \hfill \\ \end{gathered} ight. \hfill \\ \left\{ \begin{gathered} m < 0 \hfill \\ f\left( 1 ight) = \frac{{m + 5}}{{1 - m}} = - 7 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} \left\{ \begin{gathered} m > 1 \hfill \\ m = 2 \hfill \\ \end{gathered} ight.\left( {TM} ight) \hfill \\ \left\{ \begin{gathered} m < 0 \hfill \\ m = 2 \hfill \\ \end{gathered} ight.\left( {KTM} ight) \hfill \\ \end{gathered} ight.

    \Leftrightarrow m = 2 \in(0;2brack

  • Câu 11: Nhận biết

    Độ dài đường sinh

    Trong không gian, cho tam giác ABC vuông tại A, AB =a và AC = a\sqrt 3. Độ dài đường sinh \ell của hình nón nhận được khi quay tam giác ABC xung quanh trục AB bằng:

    Độ dài đường sinh

    Từ giả thiết suy ra hình nón có đỉnh là B , tâm đường tròn đáy là A , bán kính đáy là AC = a\sqrt 3 và chiều cao hình nón là AB = a.

    Vậy độ dài đường sinh của hình nón là:

    \ell = BC = \sqrt {A{B^2} + A{C^2}} = 2a.

  • Câu 12: Thông hiểu

    Xác định điểm cực đại của hàm số

    Cho hàm số y = f(x) liên tục và có đạo hàm trên \mathbb{R}, biết y = f'(x) có đồ thị như hình vẽ:

    Điểm cực đại của hàm số y = f(x) đã cho là:

    Dựa vào đồ thị hàm số y = f'(x) ta có: f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 3 \\ x = - 2 \\ x = 1 \\ x = 3 \\ \end{matrix} ight.

    Khi đó ta có bảng xét dấu f'(x) như sau:

    Dựa vào bảng xét dấu suy ra điểm cực đại của hàm số y = f(x) là x = - 2.

  • Câu 13: Thông hiểu

    Xác định giá trị của biểu thức logarit

    Với các số a, b > 0 thỏa mãn {a^2} + {b^2} = 6ab, biểu thức {\log _2}\left( {a + b} ight) bằng:

    Ta có: 

    \begin{matrix} {a^2} + {b^2} = 6ab \hfill \\ \Rightarrow {\left( {a + b} ight)^2} = 8ab \hfill \\ \Rightarrow {\log _2}{\left( {a + b} ight)^2} = {\log _2}\left( {8ab} ight) \hfill \\ \Rightarrow 2{\log _2}\left( {a + b} ight) = {\log _2}8 + {\log _2}a + {\log _2}b \hfill \\ \Rightarrow {\log _2}\left( {a + b} ight) = \dfrac{1}{2}\left( {{{\log }_2}8 + {{\log }_2}a + {{\log }_2}b} ight) \hfill \\ \Rightarrow {\log _2}\left( {a + b} ight) = \dfrac{1}{2}\left( {3 + {{\log }_2}a + {{\log }_2}b} ight) \hfill \\ \end{matrix}

  • Câu 14: Thông hiểu

    Đếm số đa diện lồi

    Cho các hình khối sau:

    Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?

    2 || Hai || hai

    Đáp án là:

    Cho các hình khối sau:

    Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số đa diện lồi là?

    2 || Hai || hai

     Có hai khối đa diện lồi là: Hình 1 & Hình 4

  • Câu 15: Vận dụng

    Ghi đáp án vào ô trống

    Cho hàm số y =f(x) liên tục, có đạo hàm trên \mathbb{R}. Đồ thị hàm số y = f'(x) như sau:

    Hàm số y = f(3 - x) nghịch biến trên khoảng (2;b). Giá trị lớn nhất của b bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y =f(x) liên tục, có đạo hàm trên \mathbb{R}. Đồ thị hàm số y = f'(x) như sau:

    Hàm số y = f(3 - x) nghịch biến trên khoảng (2;b). Giá trị lớn nhất của b bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 16: Vận dụng cao

    Ghi đáp án vào ô trống

    Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.

    Đáp án: 4054 (chục nghìn)

    Đáp án là:

    Người ta xây dựng một chân tháp bằng bê tông có dạng khối chóp cụt tứ giác đều. Cạnh đáy dưới dài 5 m, cạnh đáy trên dài 2 m, cạnh bên dài 3 m. Biết rằng chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3. Tính số tiền để mua bê tông tươi làm chân tháp theo đơn vị chục nghìn.

    Đáp án: 4054 (chục nghìn)

    Hình vẽ minh họa

    Mô hình hóa chân tháp của bài toán bằng khối chóp cụt tứ giác đều ABCD.A^{'}B^{'}C^{'}D^{'}, với O,O^{'} lần lượt là tâm của hai đáy ABCD và A^{'}B^{'}C^{'}D^{'}.

    Như vậy ta có:

    ABCD là hình vuông cạnh 5 có diện tích S_{ABCD} = 5^{2} = 25;

    A^{'}B^{'}C^{'}D^{'} là hình vuông cạnh 2 có diện tích S_{A^{'}B^{'}C^{'}D^{'}} = 2^{2} = 4;

    Các cạnh bên A^{'}A,B^{'}B,C^{'}C,D^{'}D có độ dài bằng 3;

    {OO}^{'} vuông góc với ( ABCD ) và ( \left. \ A^{'}B^{'}C^{'}D^{'} ight).

    Do ABCD là hình vuông nên \widehat{ABC} =90^{\circ}, do đó tam giác ABC vuông tại B.

    Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:

    AC^{2} = AB^{2} + BC^{2} = 5^{2} + 5^{2}= 50

    Suy ra AC = 5\sqrt{2}.
    Do đó CO = \frac{AC}{2} =\frac{5\sqrt{2}}{2} (do 0 là tâm hình vuông ABCD ).

    Do A^{'}B^{'}C^{'}D^{'} là hình vuông nên \widehat{A^{'}B^{'}C^{'}} = 90^{\circ}, do đó tam giác A^{'}B^{'}C^{'} vuông tại B^{'}.

    Áp dụng định lí Pythagore trong tam giác A^{'}B^{'}C^{'} vuông tại B^{'} có:

    A^{'}C^{'2} = A^{'}B^{'2} + B^{'}C^{'2} = 2^{2} + 2^{2} = 8.

    Suy ra A^{'}C^{'} = 2\sqrt{2}.

    Do đó C^{'}O^{'} = \frac{A^{'}C^{'}}{2} = \frac{2\sqrt{2}}{2} = \sqrt{2} (do O^{'} là tâm hình vuông A^{'}B^{'}C^{'}D^{'} ).

    Dễ thấy: (ABCD) \cap \left( A^{'}C^{'}CA ight) = AC; \left( A^{'}B^{'}C^{'}D^{'} ight) \cap \left( A^{'}C^{'}CA ight) = A^{'}C^{'}.

    Mà ( ABCD ) // ( \left. \ A^{'}B^{'}C^{'}D^{'} ight).

    Suy ra AC//A^{'}C^{'} hay A^{'}C^{'}CA là hình thang.

    Xét hình thang A^{'}C^{'}CA, kẻ C^{'}H\bot AC(H \in AC).

    Vì 00^{'}\bot(ABCD) và AC \subset (ABCD) nên 00^{'}\bot AC.

    Do đó C^{'}H//{OO}^{'} (cùng vuông góc với AC).

    Mà O^{'}C^{'}//OH (do A^{'}C^{'}//AC )

    Suy ra O^{'}C^{'}HO là hình bình hành.

    Do đó: 0O^{'} = C^{'}H và OH = C^{'}O^{'} = \sqrt{2}.

    Suy ra HC = OC - OH = \frac{5\sqrt{2}}{2} - \sqrt{2} = \frac{3\sqrt{2}}{2}.

    Áp dụng định lí Pythagore trong tam giác C^{'}HC vuông tại H( do \left. \ C^{'}H\bot AC ight) có:

    C^{'}C^{2} = C^{'}H^{2} + {HC}^{2}

    Suy ra C^{'}H = \sqrt{C^{'}C^{2} - HC^{2}} = \sqrt{3^{2} - \left( \frac{3\sqrt{2}}{2} ight)^{2}} = \frac{3\sqrt{2}}{2}.

    Do đó OO^{'} = C^{'}H = \frac{3\sqrt{2}}{2}.

    Thể tích khối chóp cụt tứ giác đều ABCD.A^{'}B^{'}C^{'}D^{'} với chiều cao OO^{'} = \frac{3\sqrt{2}}{2} và diện tích hai đáy S_{ABCD} = 25, S_{A'B'C'D'} =4 là:

    V_{ABCD \cdot A^{'}B^{'}C^{'}D^{'}} = \frac{1}{3} \cdot\frac{3\sqrt{2}}{2}(25 + \sqrt{25.4} + 4) = \frac{39\sqrt{2}}{2}\left({m}^{3} ight)

    Như vậy ta có thể tích của chân tháp đã cho bằng \frac{39\sqrt{2}}{2}\left( {m}^{3}ight).

    Vi chân tháp được làm bằng bê tông tươi với giá tiền là 1470000 đồng /m^{3} nên số tiền để mua bê tông tươi làm chân tháp là:

    \frac{39\sqrt{2}}{2}.1470000 \approx40538432 (đồng)

    Vậy số tiền để mua bê tông tươi làm chân tháp khoảng 40538432 đồng.

  • Câu 17: Nhận biết

    Đếm số nghiệm

    Số nghiệm của phương trình {\log _2}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _2}x = 0 là:

    0 || PT không có nghiệm || không có nghiệm || vô nghiệm || PT vô nghiệm

    Đáp án là:

    Số nghiệm của phương trình {\log _2}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _2}x = 0 là:

    0 || PT không có nghiệm || không có nghiệm || vô nghiệm || PT vô nghiệm

     PT \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ {x^3} + 1 > 0 \hfill \\ {x^2} - x + 1 > 0 \hfill \\ {\log _{{2^{}}}}({x^3} + 1) - {\log _2}({x^2} - x + 1) - 2{\log _{{2^{}}}}x = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \frac{{{x^3} + 1}}{{{x^2}({x^2} - x + 1)}} = 0 \hfill \\ \end{gathered} ight.  \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ \frac{{(x + 1)({x^2} - x + 1)}}{{{x^2}({x^2} - x + 1)}} = 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x + 1 = 0 \hfill \\ \end{gathered} ight. \Leftrightarrow \left\{ \begin{gathered} x > 0 \hfill \\ x = - 1 \hfill \\ \end{gathered} ight. \Rightarrow x \in \emptyset

    Vậy số nghiệm của PT là 0.

  • Câu 18: Vận dụng cao

    Tìm m thỏa mãn yêu cầu

    Tìm giá trị tham số m để đồ thị hàm số y = x^{4} - 2(m + 1)x^{2} + 2m + 3 có ba điểm cực trị A;B;C sao cho trục Ox chia tam giác ABC thành một tam giác và một hình thang biết rằng tỉ lệ diện tích tam giác nhỏ được chia ra và diện tích hình thang bằng \frac{4}{5}?

    Ta có: y' = 4x^{2} - 4(m + 1)x

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x^{2} = m + 1 \\ \end{matrix} ight.

    Hàm số có ba điểm cực trị khi và chỉ khi y' = 0 có ba nghiệm phân biệt \Leftrightarrow m > - 1

    Khi m > - 1 đồ thị hàm số có ba điểm cực trị là A(0;2m + 3), B\left( - \sqrt{m + 1}; - m^{2} + 2 ight), C\left( \sqrt{m + 1}; - m^{2} + 2 ight)

    Ta có: A \in Oy, B và C đối xứng với nhau qua Oy suy ra tam giác ABC cân tại A

    Hình vẽ minh họa

    Trục hoành chia tam giác ABC thành một tam giác và một hình thang \Rightarrow \left\{ \begin{matrix} 2m + 3 > 0 \\ - m^{2} + 2 < 0 \\ \end{matrix} ight.

    \Rightarrow \left\{ \begin{gathered} m > - \dfrac{3}{2} \hfill \\ \left[ \begin{gathered} m > \sqrt 2 \hfill \\ m < - \sqrt 2 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Rightarrow \left\{ \begin{gathered} m > \sqrt 2 \hfill \\ - \dfrac{3}{2} < m < - \sqrt 2 \hfill \\ \end{gathered} ight.

    Kết hợp với điều kiện m > - 1 ta được m > \sqrt{2}

    Khi đó gọi D; E lần lượt là giao điểm của Ox và các cạnh AB; AC. Gọi K là giao điểm của BC và Oy

    Ta có:

    \frac{S_{ADE}}{S_{ABC}} = \left( \frac{OA}{AK} ight)^{2} = \left( \frac{y_{A}}{y_{A} - y_{B}} ight)^{2} = \left( \frac{2m + 3}{m^{2} + 2m + 1} ight)^{2}

    Mà \frac{S_{ADE}}{S_{ABC}} = \frac{4}{9} \Leftrightarrow \left( \frac{2m + 3}{m^{2} + 2m + 1} ight)^{2} = \frac{4}{9}

    Vì m > \sqrt{2} \Leftrightarrow \frac{2m + 3}{m^{2} + 2m + 1} = \frac{2}{3}

    \Leftrightarrow 2m^{2} - 2m - 7 = 0\Leftrightarrow \left\lbrack \begin{matrix}m = \dfrac{1 + \sqrt{15}}{2} \\m = \dfrac{1 - \sqrt{15}}{2} \\\end{matrix} ight.\ \Rightarrow m = \dfrac{1 +\sqrt{15}}{2}.

  • Câu 19: Vận dụng

    Chọn đáp án đúng

    Một người gửi vào ngân hàng 200 triệu đồng vào tài khoản tiết kiệm ngân hàng với lãi suất 0,6%/ tháng, cứ sau mỗi tháng người đó rút ra 500 nghìn đồng. Hỏi sau đúng 36 lần rút tiền thì số tiền còn lại trong tài khoản của người đó gần nhất với phương án nào sau đây? (Biết rằng lãi suất không thay đổi và tiền lại mỗi tháng tính theo số tiền thực tế trong tài khoản của tháng đó?

    Số tiền còn lại trong tài khoản sau tháng thứ 1 là: 200.1,006 - 0,5 (triệu đồng)

    Số tiền còn lại trong tài khoản sau tháng thứ 2 là:

    \left( {200.1,006 - 0,5} ight).1,006 - 0,5 = 200.{\left( {1,006} ight)^2} - 0,5\left( {1 + 1,006} ight) (triệu đồng)

    Số tiền còn lại trong tài khoản sau tháng thứ 3 là:

    200.{\left( {1,006} ight)^3} - 0,5\left[ {1 + 1,006 + {{\left( {1,006} ight)}^2}} ight] (triệu đồng)

    Cứ tiếp tục quá trình thì số tiền còn lại trong tài khoản sau tháng thứ 36 là:

    200.{\left( {1,006} ight)^3} - 0,5\left[ {1 + 1,006 + {{\left( {1,006} ight)}^2} + ... + {{\left( {1,006} ight)}^{35}}} ight]

    = 200.{\left( {1,006} ight)^{36}} - 0,5.\frac{{1 - {{\left( {1,006} ight)}^{36}}}}{{1 - 1,006}} = 228,035 (triệu đồng) 

  • Câu 20: Thông hiểu

    Rút gọn biểu thức T

    Thu gọn biểu thức T = \frac{{{a^{\frac{7}{6}}}.{b^{ - \frac{2}{3}}}}}{{\sqrt[6]{{a{b^2}}}}} biết a và b là hai số thực dương.

    Ta có: T = \frac{{{a^{\frac{7}{6}}}.{b^{ - \frac{2}{3}}}}}{{\sqrt[6]{{a{b^2}}}}} = \left( {{a^{\frac{7}{6}}}:{a^{\frac{1}{6}}}} ight).\left( {{b^{\frac{{ - 2}}{3}}}:{b^{\frac{2}{6}}}} ight) = \frac{a}{b}

  • Câu 21: Thông hiểu

    Tính tang của góc

    Cho hình nón có đỉnh S, đường cao SO = h, đường sinh SA. Nội tiếp hình nón là một hình chóp đỉnh S, đáy là hình vuông ABCD cạnh a. Nửa góc ở đỉnh của hình nón có tan bằng:

     Tính tang của góc

    Nửa góc ở đỉnh của hình nón là góc \widehat {ASO} .

    Hình vuông ABCD cạnh a nên suy ra: OA = \frac{{a\sqrt 2 }}{2}

    Trong tam giác vuông SOA, ta có \tan \widehat {ASO} = \frac{{OA}}{{SO}} = \frac{{a\sqrt 2 }}{{2h}}.

  • Câu 22: Vận dụng

    Chọn đáp án đúng:

    Đường thẳng y = kx + m vừa là tiếp tuyến của đường cong y = \frac{x+2}{2x+3}, vừa cắt hai trục toạ độ A, B sao cho tam giác OAB cân tại gốc tạo độ O. Tính giá trị của biểu thức S = m + k

  • Câu 23: Thông hiểu

    Chọn đáp án đúng

    Cho hàm số y = \frac{ax + b}{cx - 1} có đồ thị như hình vẽ bên dưới. Trong các hệ số a, b, c có bao nhiêu số dương?

    Tiệm cận đứng: x = \frac{1}{c} = 1 \Leftrightarrow c = 1

    Tiệm cận ngang: y = \frac{a}{c} = - 1\Leftrightarrow a = - c \Rightarrow a = - 1

    Đồ thị cắt trục hoành tại x = 2 nên 2a + b = 0 hay b = - 2a = 2.

    Vậy trong các hệ số a, b, c có có hai số dương là b,c.

  • Câu 24: Nhận biết

    Điền đáp án

    Điều kiện xác định của bất phương trình {\log _{0,5}}(5{\text{x}} + 15) \leqslant {\log _{0,5}}\left( {{x^2} + 6{\text{x}} + 8} ight) là:

    x>-2|| X>-2 || x lớn hơn -2

    Đáp án là:

    Điều kiện xác định của bất phương trình {\log _{0,5}}(5{\text{x}} + 15) \leqslant {\log _{0,5}}\left( {{x^2} + 6{\text{x}} + 8} ight) là:

    x>-2|| X>-2 || x lớn hơn -2

     Điều kiện: \left\{ \begin{gathered} 5x + 15 > 0 \hfill \\ {x^2} + 6{\text{x}} + 8 > 0 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\{ \begin{gathered} x > - 3 \hfill \\ \left[ \begin{gathered} x > - 2 \hfill \\ x < - 4 \hfill \\ \end{gathered} ight. \hfill \\ \end{gathered} ight. \Leftrightarrow x > - 2

    Vậy để BPT xác định khi và chỉ khi x > - 2.

  • Câu 25: Nhận biết

    Tìm giá trị của n

    Cho 0 < a e 1 và biểu thức \sqrt {a.\sqrt[3]{a}} viết dưới dạng {a^n}. Giá trị của n là:

    Ta có:

    \sqrt {a.\sqrt[3]{a}} = {\left( {a.{a^{\frac{1}{3}}}} ight)^{\frac{1}{2}}} = {\left( {{a^{\frac{4}{3}}}} ight)^{\frac{1}{2}}} = {a^{\frac{2}{3}}}

    Vậy n = \frac{2}{3}

  • Câu 26: Nhận biết

    Chọn đáp án thích hợp

    Cho hàm số y = \frac{ax^{2} + bx + c}{mx + n},(am eq 0) có đồ thị như hình vẽ. Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là:

    Dựa vào đồ thị hàm số, ta thấy đường tiệm cận xiên của đồ thị hàm số đi qua 2 điểm (1;1) và ( - 1; - 1) nên đường tiệm cận xiên của đồ thị hàm số có phương trình y = x.

  • Câu 27: Nhận biết

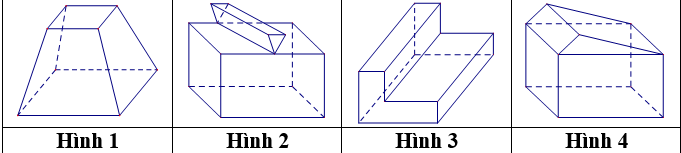
    Tìm hình đa diện

    Cho các hình sau: 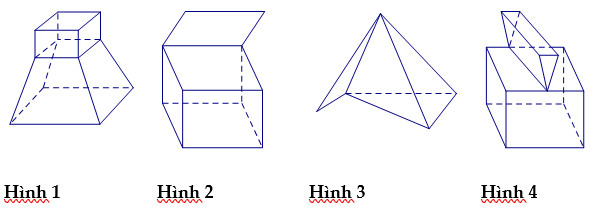Tìm hình đa diện

    Mỗi hình sau gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

    Áp dụng định nghĩa hình đa diện, ta có:

    “Hình đa diện (còn gọi tắt là đa diện) là hình được tạo bởi một số hữu hạn các đa giác, gọi là các mặt của hình đa diện, thỏa mãn các tính chất sau:

    TC1: Hai mặt phân biệt chỉ có thể hoặc không giao nhau hoặc có một đỉnh chung, hoặc có một cạnh chung.

    TC2: Mỗi cạnh thuộc một mặt là cạnh cung của đúng hai mặt.

    TC3: Cho hai mặt S và S’, luôn tồn tại một dãy các mặt {S_0},{S_1},...\,\,,{S_n} sao cho trùng với trùng với S’ và bất kì hai mặt {S_i},{S_{i + 1}} nào (0 \le i \le n - 1) cũng đều có một cạnh chung.

    Các đỉnh, cạnh của mặt theo thứ tự được gọi là các đỉnh, cạnh của hình đa diện.”

  • Câu 28: Vận dụng

    Tìm nghiệm nguyên MIN

    Nghiệm nguyên nhỏ nhất của bất phương trình {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0  là:

    x=4 || X=4|| x bằng 4

    Đáp án là:

    Nghiệm nguyên nhỏ nhất của bất phương trình {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0  là:

    x=4 || X=4|| x bằng 4

    Theo bài toán, ta xét điều kiện của BPT là: x > 0;x e 1;x e 3.

    Ta có: {\log _x}3 - {\log _{\frac{x}{3}}}3 < 0 \Leftrightarrow \frac{{ - 1}}{{{{\log }_3}x.\left( {{{\log }_3}x - 1} ight)}} < 0

    \Leftrightarrow \left[ \begin{gathered} {\log _3}x < 0 \hfill \\ {\log _3}x > 1 \hfill \\ \end{gathered} ight. \Leftrightarrow \left[ \begin{gathered} 0 < x < 1 \hfill \\ x > 3 \hfill \\ \end{gathered} ight.

  • Câu 29: Vận dụng

    Thể tích lăng trụ xiên có đáy tam giác vuông cân

    Cho hình lăng trụ tam giác ABC có đáy ABC là tam giác vuông cân tại A, cạnh AC = 2\sqrt 2. Biết AC' tạo với mặt phẳng (ABC) một góc 60^0 và AC'=4. Tính thể tích V của khối đa diện ABCB'C'. 

     

    Gọi H là hình chiếu của C' trên mặt phẳng (ABC).

    Suy ra AH là hình chiếu của AC' trên mặt phẳng (ABC).

    Do đó {60^0} = \widehat {AC',\left( {ABC} ight)} = \widehat {\left( {AC',AH} ight)} = \widehat {HAC'}

    Tam giác vuông AHC', có  C'H = AC'.\sin \widehat {HAC'} = 2\sqrt 3

    Thể tích khối lăng trụ {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.C'H = 8\sqrt 3

    Suy ra thể tích cần tính là:

     {V_{ABCB'C'}} = \frac{2}{3}{V_{ABC.A'B'C'}} = \frac{{16\sqrt 3 }}{3}.

  • Câu 30: Thông hiểu

    Giá trị biểu thức A

    Cho a,b,c > 0. Tính giá trị của biểu thức A = {\log _a}\left( {{b^2}} ight).{\log _b}\left( {\sqrt {bc} } ight) - {\log _a}\left( c ight)

    Ta có:

    \begin{matrix} A = {\log _a}\left( {{b^2}} ight).{\log _b}\left( {\sqrt {bc} } ight) - {\log _a}\left( c ight) \hfill \\ A = 2{\log _a}\left( b ight).\dfrac{1}{2}.{\log _b}\left( {bc} ight) - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight).{\log _b}\left( {bc} ight) - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight).\left[ {{{\log }_b}\left( b ight) + {{\log }_b}\left( c ight)} ight] - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight).\left[ {1 + {{\log }_b}\left( c ight)} ight] - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight) + {\log _a}\left( b ight).{\log _b}\left( c ight) - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight) + {\log _a}\left( c ight) - {\log _a}\left( c ight) \hfill \\ A = {\log _a}\left( b ight) \hfill \\ \end{matrix}

  • Câu 31: Vận dụng cao

    Tìm tất cả các tập giá trị của a

    Tìm tất cả các tập giá trị của a để  \sqrt[{21}]{{{a^5}}} > \sqrt[7]{{{a^2}}}?

    Ta có: \sqrt[7]{{{a^2}}} = \sqrt[{21}]{{{a^6}}}

    => \sqrt[{21}]{{{a^5}}} > \sqrt[7]{{{a^2}}} \Rightarrow \sqrt[{21}]{{{a^5}}} > \sqrt[{21}]{{{a^6}}}

    Mà 5 < 6 => 0 < a < 1

  • Câu 32: Nhận biết

    Xác định số nghiệm của phương trình

    Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình f(x) = - \frac{3}{2} là

    Từ đồ thị ta f(x) = - \frac{3}{2} có 4 nghiệm phân biệt

  • Câu 33: Nhận biết

    Biến đổi biểu thức

    Với a và b là hai số thực dương tùy ý thì \log \left( {a{b^2}} ight) bằng:

    Ta có: \log \left( {a{b^2}} ight) = \log a + \log {b^2} = \log a + 2\log b

  • Câu 34: Nhận biết

    Hình nào không phải khối đa diện lồi

    Trong các hình dưới đây hình nào không phải khối đa diện lồi?

     

    Đường nối đoạn MN không thuộc khối hình 4 nên hình 4 không phải khối đa diện lồi.

  • Câu 35: Vận dụng

    Chọn mệnh đề đúng

    Biết rằng hàm số y = (x + a)^{3} + (x +b)^{3} - x^{3} có hai điểm cực trị. Mệnh đề nào sau đây là đúng?

    Ta có y' = 3(x + a)^{2} + 3(x +b)^{2} - 3x^{2},\ \ \forall x\mathbb{\in R}.

    Có y' = 0 \Leftrightarrow (x + a)^{2}+ (x + b)^{2} - x^{2} = 0

    \Leftrightarrow x^{2} + 2(a + b)x + a^{2} + b^{2} = 0 (*)

    Để hàm số đã cho đạt cực đại, cực tiểu khi và chỉ khi (*) có hai nghiệm phân biệt

    \Leftrightarrow \Delta' = (a + b)^{2} - \left( a^{2} + b^{2} ight) > 0 \Leftrightarrow ab > 0.

  • Câu 36: Thông hiểu

    Phương trình trở thành

    Nếu đặt t = {\log _2}x thì phương trình \frac{1}{{5 - {{\log }_2}x}} + \frac{2}{{1 + {{\log }_2}x}} = 1 trở thành phương trình nào?

    Đặt t = {\log _2}x

    PT \Leftrightarrow \frac{1}{{5 - t}} + \frac{2}{{1 + t}} = 1 \Leftrightarrow \frac{{1 + t + 2(5 - t)}}{{(5 - t)(1 + t)}} = 1

    \Leftrightarrow 1 + t + 2(5 - t) = (5 - t)(1 + t)

    \Leftrightarrow 11 - t = 5 + 4t - {t^2} \Leftrightarrow {t^2} - 5t + 6 = 0.

  • Câu 37: Nhận biết

    Chọn khẳng định đúng

    Cho hàm số y = - \frac{1}{3}x^{3} + \frac{1}{2}x^{2} + 6x - 1. Khẳng định nào sau đây đúng?

    Tập xác định D\mathbb{= R}

    Ta có: y' = - x^{2} + x + 6 \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 2 \\ x = 3 \\ \end{matrix} ight.

    Ta có bảng xét dấu

    Suy ra hàm số đồng biến trên khoảng ( - 2,3).

  • Câu 38: Nhận biết

    Hàm số nào nghịch biến trên tập số thực?

    Trong các hàm số sau, hàm số nào nghịch biến trên tập số thực?

     Ta có:

    y = {\log _{\frac{\pi }{4}}}\left( {2{x^2} + 1} ight);y = {\log _{\frac{1}{2}}}x là các hàm số không xác định trên \mathbb{R}

    Vì \frac{2}{e} < 1 \Rightarrow y = {\left( {\frac{2}{e}} ight)^x} nghịch biến trên \mathbb{R}

  • Câu 39: Thông hiểu

    Tìm hàm số tương ứng với đồ thị hàm số

    Hàm số nào sau đây phù hợp với hình vẽ:

    Tìm hàm số tương ứng với đồ thị hàm số

     Ta có: y\left( 1 ight) = 0 và hàm số đồng biến trên \left( {0; + \infty } ight) nên chỉ có hàm số y = {\log _{\sqrt 6 }}x thỏa mãn

  • Câu 40: Thông hiểu

    Định giá trị lớn nhất của hàm số chứa căn

    Tìm giá trị lớn nhất M của hàm số f(x) = \sqrt{x - 2} + \sqrt{4 - x}.

    TXĐ: D = \lbrack 2;4brack.

    Đạo hàm f(x) = \frac{1}{2\sqrt{x - 2}} - \frac{1}{2\sqrt{4 - x}}

    \Rightarrow f'(x) = 0 \Leftrightarrow x = 3 \in \lbrack 2;4brack

    Ta có \left\{ \begin{matrix} f(2) = \sqrt{2} \\ f(3) = 2 \\ f(4) = \sqrt{2} \\ \end{matrix} ight.\ ightarrow M = 2.

  • Câu 41: Vận dụng cao

    Mệnh đề đúng

    Cho hình bát diện đều cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình bát diện đó. Mệnh đề nào dưới đây đúng?

     

    Hình bát diện đều là hình có tám mặt bằng nhau và mỗi mặt là một tam giác đều. Gọi S_0 là diện tích tam giác đều cạnh a \xrightarrow{{}}\,{S_0} = \frac{{{a^2}\sqrt 3 }}{4}

    Vậy diện tích S cần tính là: S = 8.{S_0} = 8.\frac{{{a^2}\sqrt 3 }}{4} = 2\sqrt 3 \,{a^2}.

  • Câu 42: Vận dụng

    Xác định giá trị lớn nhất của hàm số

    Cho hàm số f\left( x ight) = \frac{{x - {m^2}}}{{x + 8}} (với m là tham số thực). Tìm giá trị lớn nhất của tham số m để hàm số có giá trị nhỏ nhất bằng -2 trên đoạn [0; 3].

    Xét hàm số f\left( x ight) = \frac{{x - {m^2}}}{{x + 8}} trên đoạn [0; 3] ta có:

    f'\left( x ight) = \frac{{8 + {m^2}}}{{{{\left( {x + 8} ight)}^2}}} > 0;\forall x \in \left[ {0;3} ight]

    => Hàm số f(x) đồng biến trên (0; 3)

    => \mathop {\min }\limits_{\left[ {0;3} ight]} f\left( x ight) = f\left( 0 ight) = \frac{{ - {m^2}}}{8}

    Theo bài ra ta có:

    \begin{matrix} \mathop {\min }\limits_{\left[ {0;3} ight]} f\left( x ight) = - 2 \hfill \\ \Leftrightarrow - \dfrac{{{m^2}}}{8} = - 2 \hfill \\ \Leftrightarrow {m^2} = 16 \Leftrightarrow m = \pm 4 \hfill \\ \Rightarrow {m_{\max }} = 4 \hfill \\ \end{matrix}

  • Câu 43: Vận dụng

    Tính giá trị của biểu thức T

    Cho các số thức a, b thỏa mãn 1 < a < b và {\log _a}b + {\log _b}{a^2} = 3. Tính giá trị của biểu thức T = {\log _{ab}}\frac{{{a^2} + b}}{2}

     Ta có:

    {\log _a}b + {\log _b}{a^2} = 3 \Leftrightarrow {\log _a}b + 2{\log _b}a = 3\left( * ight)

    Đặt t = {\log _a}b. Do 1 < a < b \Rightarrow t > {\log _a}b \Rightarrow t > 1

    Khi đó t + \frac{2}{t} = 3 \Leftrightarrow {t^2} - 3t + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = 1\left( {ktm} ight)} \\ {t = 2\left( {tm} ight)} \end{array}} ight.

    Với t = 2 ta có: {\log _a}b = 2 \Rightarrow b = {a^2}

    => T = {\log _{ab}}\frac{{{a^2} + b}}{2} = {\log _{{a^3}}}{a^2} = \frac{2}{3}{\log _a}a = \frac{2}{3}

  • Câu 44: Nhận biết

    V lăng trụ đứng

    Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và AC = a\sqrt 2. Tính thể tích của khối lăng trụ đã cho.

     

    Tam giác ABC vuông cân tại B,

    suy ra BA = BC = \frac{{AC}}{{\sqrt 2 }} = a \Rightarrow {S_{\Delta ABC}} = \frac{{{a^2}}}{2}

    Vậy thể tích khối lăng trụ V = {S_{\Delta ABC}}.BB' = \frac{{{a^3}}}{2}

  • Câu 45: Vận dụng cao

    Xét tính đúng sai của các nhận định

    Nhà máyA chuyên sản xuất một loại sản phẩm cho nhà máyB. Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B. Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là P(x) = 45 - 0,001x^{2}. Cho phí để A sản xuất x tấn sản phẩm trong một tháng là C(x) = 100 + 30x triệu đồng. Xét tính đúng sai của các khẳng định dưới đây:

    a) Chi phí để A sản xuất 10 tấn sản phẩm trong một tháng là 400 triệu đồng. Đúng||Sai

    b) Số tiền A thu được khi bán 10 tấn sản phẩm cho B là 600 triệu đồng. Sai||Đúng

    c) Lợi nhuận mà A thu được khi bán x tấn sản phẩm (0 \leq x \leq 100) cho B là H(x) = - 0,001x^{3} + 15x - 100. Đúng||Sai

    d) A bán cho B khoảng 70,7 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất. Đúng||Sai

    Đáp án là:

    Nhà máyA chuyên sản xuất một loại sản phẩm cho nhà máyB. Hai nhà máy thỏa thuận rằng, hằng tháng A cung cấp cho B số lượng sản phẩm theo đơn đặt hàng của B. Nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là P(x) = 45 - 0,001x^{2}. Cho phí để A sản xuất x tấn sản phẩm trong một tháng là C(x) = 100 + 30x triệu đồng. Xét tính đúng sai của các khẳng định dưới đây:

    a) Chi phí để A sản xuất 10 tấn sản phẩm trong một tháng là 400 triệu đồng. Đúng||Sai

    b) Số tiền A thu được khi bán 10 tấn sản phẩm cho B là 600 triệu đồng. Sai||Đúng

    c) Lợi nhuận mà A thu được khi bán x tấn sản phẩm (0 \leq x \leq 100) cho B là H(x) = - 0,001x^{3} + 15x - 100. Đúng||Sai

    d) A bán cho B khoảng 70,7 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất. Đúng||Sai

    a) Đúng

    b) Sai

    c) Đúng

    d) Đúng

    a) Chi phí để A sản xuất 10 tấn sản phẩm trong một tháng là C(10) = 100 + 30.10 = 400triệu đồng. Do đó a) đúng.

    b) Số tiền A thu được khi bán 10 tấn sản phẩm cho B là R(10) = 10.P(10) = 10.\left( 45 - 0,001.10^{2} \right) = 449 triệu đồng. Do đó b) sai.

    c) Lợi nhuận mà A thu được là:

    H(x) = R(x) - C(x) = xP(x) - C(x) = P(x)

    =45x - 0,001x^{3} - (100 + 30x) = - 0,001x^{3} + 15x - 100

    Do đó c) đúng.

    d) Xét hàm số H(x) = - 0,001x^{3} + 15x - 100, (0 \leq x \leq 100) ta có:

    H'(x) = - 0,003x^{2} + 15, H'(x) = 0\Leftrightarrow - 0,003x^{2} +15 = 0\Leftrightarrow x = 50\sqrt{2} .

    Ta có H(0) = - 100; H\left( 50\sqrt{2} \right) = 500\sqrt{2} - 100; H(100) = 400.

    Vậy A bán cho B khoảng 50\sqrt{2} \approx 70,7 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng H\left( 50\sqrt{2} \right) = 500\sqrt{2} - 100. Do đó d) đúng.

  • Câu 46: Thông hiểu

    Định m để hàm số đồng biến trên R

    Tìm tất cả các giá trị của tham số m để hàm số y = (m - 1)x^{3} - 3(m - 1)x^{2} + 3x + 2; (m là tham số) đồng biến trên tập số thực?

    Ta có: y' = 3(m - 1)x^{2} - 6(m - 1)x + 3

    Hàm số đã cho đồng biến trên \mathbb{R} khi và chỉ khi y' \geq 0;\forall x\mathbb{\in R}

    \Leftrightarrow \left\lbrack \begin{matrix} m - 1 = 0 \\ \left\{ \begin{matrix} m - 1 > 0 \\ \Delta' \leq 0 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ \left\{ \begin{matrix} m > 1 \\ 9(m - 1)^{2} - 9(m - 1) \leq 0 \\ \end{matrix} ight.\ \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ \left\{ \begin{matrix} m > 1 \\ 1 \leq m \leq 2 \\ \end{matrix} ight.\ \\ \end{matrix} ight.\ \Leftrightarrow 1 \leq m \leq 2

    Vậy đáp án cần tìm là 1 \leq m \leq 2.

  • Câu 47: Vận dụng cao

    Định giá trị gần nhất với kết quả

    Cho a,b,c là ba số thực dương, a > 1 thỏa mãn:

    \log_{a}^{2}(bc) + \log_{a}\left(b^{3}c^{3} + \dfrac{bc}{4} ight)^{2} + 4 + \sqrt{9 - c^{2}} =0

    Khi đó, giá trị của biểu thức T = a + 3b + 2c gần với giá trị nào nhất sau đây?

    Áp dụng bất đẳng thức (x + y)^{2} \geq 4xy, ta được:

    \left( b^{3}c^{3} + \dfrac{bc}{4}ight)^{2} \geq b^{4}c^{4} \Rightarrow \log_{a}\left( b^{3}c^{3} +\dfrac{bc}{4} ight)^{2} \geq 4\log_a(bc)

    Do đó với \forall a > 1,b,c > 0

    \log _a^2(bc) + {\log _a}{\left( {{b^3}{c^3} + \frac{{bc}}{4}} ight)^2} + 4 + \sqrt {9 - {c^2}}\geqslant \log _a^2(bc) + 4{\log _a}(bc) + 4 + \sqrt {9 - {c^2}}

    \Leftrightarrow \log _a^2(bc) + {\log _a}{\left( {{b^3}{c^3} + \frac{{bc}}{4}} ight)^2} + 4 + \sqrt {9 - {c^2}}\geqslant {\left[ {{{\log }_a}(bc) + 2} ight]^2} + \sqrt {9 - {c^2}} \geqslant 0

    Dấu “=” xảy ra khi \left\{ \begin{matrix}b^{3}c^{3} = \dfrac{bc}{4} \\\log_{a}(bc) = - 2 \\c^{2} = 9 \\a > 1 \\b > 0 \\c > 0 \\\end{matrix} ight.\ \Rightarrow \left\{ \begin{matrix}a = \sqrt{2} \\b = \dfrac{1}{6} \\c = 3 \\\end{matrix} ight.

    Khi đó T = a + 3b + 2c = \sqrt{2} + \frac{1}{2} + 6 \approx 7,91.

    Vậy giá trị của T gần 8 nhất.

  • Câu 48: Thông hiểu

    Tìm tâm mặt cầu

    Cho các điểm A(1;3;0) và B(2;1;1) và đường thẳng d:\frac{x}{2} = \frac{y - 3}{1} = \frac{z}{1}. Mặt cầu (S)đi qua hai điểm A, B và tâm thuộc đường thẳng d thì tọa độ tâm của (S) là:

    Gọi I(2t;3 + t;t) trên d vì IA = IB \Rightarrow t = 4 \Rightarrow I(8;7;4).

  • Câu 49: Thông hiểu

    Xét tính đúng sai của các khẳng định

    Cho x,y là các số thực thỏa mãn f(x,y) = \log_{4}(x + y) + \log_{4}(x - y)\geq 1\ \ (*) . Các khẳng định sau đúng hay sai?

    a) Điều kiện xác định của hàm số f(x,y) là \left\{ \begin{matrix} x + y > 0 \\ x - y > 0 \\ \end{matrix} ight. . Đúng||Sai

    b) Với cặp số x,y thỏa mãn điều kiện xác định của hàm số f(x,y) , ta có: f(x,y) = x^{2} - y^{2} . Sai||Đúng

    c) Cặp số \left\{ \begin{matrix} x = 8 \\ y = 16 \\ \end{matrix} ight. thỏa mãn f(x,y) = \log_{4}(x + y) + \log_{4}(x - y) \geq 1 . Sai||Đúng

    d) Với P = 2x - y thì P_{\min} = 2\sqrt{3} . Đúng||Sai

    Đáp án là:

    Cho x,y là các số thực thỏa mãn f(x,y) = \log_{4}(x + y) + \log_{4}(x - y)\geq 1\ \ (*) . Các khẳng định sau đúng hay sai?

    a) Điều kiện xác định của hàm số f(x,y) là \left\{ \begin{matrix} x + y > 0 \\ x - y > 0 \\ \end{matrix} ight. . Đúng||Sai

    b) Với cặp số x,y thỏa mãn điều kiện xác định của hàm số f(x,y) , ta có: f(x,y) = x^{2} - y^{2} . Sai||Đúng

    c) Cặp số \left\{ \begin{matrix} x = 8 \\ y = 16 \\ \end{matrix} ight. thỏa mãn f(x,y) = \log_{4}(x + y) + \log_{4}(x - y) \geq 1 . Sai||Đúng

    d) Với P = 2x - y thì P_{\min} = 2\sqrt{3} . Đúng||Sai

    a) Điều kiện để bất phương trình có nghĩa là \left\{ \begin{matrix} x + y > 0 \\ x - y > 0 \\ \end{matrix} ight., suy ra mệnh đề đúng.

    b) Ta có f(x,y) = \log_{4}(x + y) +\log_{4}(x - y) = \log_{4}\left( x^{2} - y^{2} ight), suy ra mệnh đề sai.

    c) Ta thấy x - y = 8 - 16 = - 8 < 0, suy ra mệnh đề sai.

    d) Ta có: \log_{4}(x + y) + \log_{4}(x - y)\geq 1

    \Leftrightarrow x^{2} - y^{2} \geq 4 \Rightarrow x \geq \sqrt{y^{2} + 4}

    Do đó P \geq 2\sqrt{y^{2} + 4} - y = f(y).

    Khi đó P' = \frac{2y}{\sqrt{y^{2} + 4}} - 1 = 0\overset{y > 0}{ightarrow}y = \frac{2}{\sqrt{3}}

    Suy ra P_{\min} = 2\sqrt{3}. suy ra mệnh đề đúng.

  • Câu 50: Thông hiểu

    Chọn mệnh đề đúng

    Cho hàm số y = f(x) có đồ thị là đường cong (C) và các giới hạn \lim_{x \rightarrow 2^{+}}f(x) = 1; \lim_{x \rightarrow 2^{-}}f(x) = 1; \lim_{x \rightarrow - \infty}f(x) = 2; \lim_{x \rightarrow + \infty}f(x) = 2. Hỏi mệnh đề nào sau đây đúng?

    Ta có: \left\{ \begin{matrix} \lim_{x \rightarrow - \infty}f(x) = 2 \\ \lim_{x \rightarrow + \infty}f(x) = 2 \end{matrix} \right. \Rightarrow đường thẳng y = 2 là tiệm cận ngang của (C).

Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé!
Mua ngay Đổi điểm
Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Đề thi học kì 1 Toán 12 Đề 2 Kết quả
  • Thời gian làm bài: 00:00:00
  • Số câu đã làm: 0
  • Điểm tạm tính: 0
  • Điểm thưởng: 0
Xem đáp án Làm lại

Đấu trường Đề thi học kì 1 Toán 12 Đề 2

Đang tìm đối thủ...

Đang tải...

Tạo phòng ngay Đấu trường chung
1
23 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Đề thi học kì 1 Toán 12 Đề 2
Thời gian còn lại 90:00 Số câu đã làm 0/50
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
Chưa làm Đã làm
Làm lại Nộp bài
Tìm bài trong mục này