Bất phương trình mũ
Bài học Lí thuyết toán 12: Bất phương trình mũ giới thiệu cho các em khái niệm bất phương trình mũ cơ bản và cách giải bất phương trình mũ. Bên cạnh đó là các ví dụ bài tập có lời giải chi tiết giúp các em dễ dàng ôn tập củng cố.
1. Khái niệm
1.1. Định nghĩa
- Bất phương trình mũ cơ bản có dạng
\({a^x} > b\) (hoặc \({a^x} \geqslant b,{a^x} < b,{a^x} \leqslant b\)) với \(a > 0,a \ne 1\). - Để giải, ta xét bất phương trình có dạng \({a^x} > b\)
- Nếu \(b \leq 0\), tập nghiệm của bất phương trình là \(\mathbb{R}\), vì \({a^x} > b,\forall x \in \mathbb{R}\)
- Nếu \(b > 0\) thì bất phương trình tương đương với \({a^x} > {a^{{{\log }_a}b}}\), khi đó:
+) Với \(a>1\), nghiệm của bất phương trình là \(x > {\log _a}b\)
+) Với \(0 < a < 1\), nghiệm của bất phương trình là \(x < {\log _a}b\)
Ví dụ: Tập nghiệm của bất phương trình \({\left( {\frac{1}{2}} \right)^x} > 32\) là:
\({\left( {\frac{1}{2}} \right)^x} > 32\) \(\Leftrightarrow {\left( {\frac{1}{2}} \right)^x} > {\left( {\frac{1}{2}} \right)^{ - 5}}\)\(\Leftrightarrow x < - 5\)
1.2. Đồ thị minh họa
Ta minh họa bằng đồ thị sau:
- Với \(a>1\), ta có đồ thị sau.
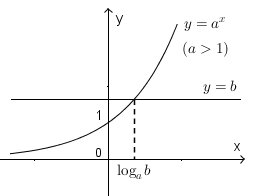
- Với \(0 < a < 1\), ta có đồ thị sau.
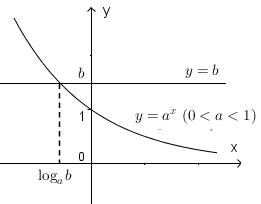
2. Cách giải bất phương trình mũ
- Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.
\(\boxed{{a^{f\left( x \right)}} > {a^{g\left( x \right)}} \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
a > 1 \hfill \\
f\left( x \right) > g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
0 < a < 1 \hfill \\
f\left( x \right) < g\left( x \right) \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.}\)
- Tương tự với bất phương trình dạng:
\(\left[ \begin{gathered}
{a^{f\left( x \right)}} \geqslant {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} < {a^{g\left( x \right)}} \hfill \\
{a^{f\left( x \right)}} \leqslant {a^{g\left( x \right)}} \hfill \\
\end{gathered} \right.\)
- Trong trường hợp cơ số \(a\) có chứa ẩn số thì:
\(\boxed{{a^M} > {a^N} \Leftrightarrow \left( {a - 1} \right)\left( {M - N} \right) > 0}\).
- Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ: đưa về cùng cơ số; đặt ẩn phụ.
- Sử dụng tính đơn điệu:
\(\left\{ \begin{gathered} y = f\left( x \right) \mbox{ đồng biến trên D thì } f\left( u \right) < f\left( v \right) \Rightarrow u < v \hfill \\ y = f\left( x \right) \text{ nghịch biến trên D thì } f\left( u \right) < f\left( v \right) \Rightarrow u > v \hfill \\ \end{gathered} \right.\)
Ví dụ: Tập nghiệm của bất phương trình \({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)là?
Giải:
Ta có: \({2^x} + {2^{x + 1}} \leqslant {3^x} + {3^{x - 1}}\)
\(\Leftrightarrow {3.2^x} \leqslant \frac{4}{3}{.3^x}\)\(\Leftrightarrow {\left( {\frac{3}{2}} \right)^x} \geqslant \frac{9}{4}\)
\(\Leftrightarrow x \geqslant 2\)
Vậy bất phương trình có tập nghiệm là \(x \in \left[ {2; + \infty } \right)\)
