Mặt trụ tròn xoay
Bài học Lí thuyết toán 12: Mặt trụ tròn xoay là phần kiến thức trong Khái niệm mặt tròn xoay, giới thiệu cho các em các định nghĩa mặt trụ, hình trụ tròn xoay, công thức tính diện tích, thể tích và thiết diện khi cắt mặt trụ.
1. Mặt trụ tròn xoay
Định nghĩa:
Trong 
\((P)\) cho hai đường thẳng \(\Delta\) và \(l\) song song nhau, cách nhau một khoảng \(r\). Khi quay \((P)\) quanh trục cố định \(\Delta\) thì đường thẳng \(l\) sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.
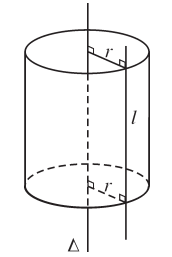
Nhận xét:
- Đường thẳng \(\Delta\) được gọi là trục.
- Đường thẳng \(l\) được gọi là đường sinh.
- Khoảng cách \(r\) được gọi là bán kính của mặt trụ.
2. Hình trụ tròn xoay
Định nghĩa:
Khi quay hình chữ nhật \(ABCD\) xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh \(AB\) thì đường gấp khúc \(ABCD\) tạo thành một hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.
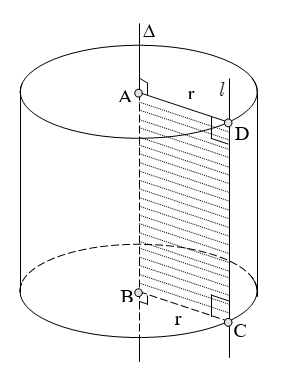
Nhận xét:
- Đường thẳng \(AB\) được gọi là trục.
- Đoạn thẳng \(CD\) được gọi là đường sinh.
- Độ dài đoạn thẳng \(AB=CD=h\) được gọi là chiều cao của hình trụ.
- Hình tròn tâm \(A\), bán kính \(r=AD\) và hình tròn tâm \(B\), bán kính \(r=BC\) được gọi là 2 đáy của hình trụ.
- Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ.
3. Công thức tính diện tích và thể tích
Cho hình trụ có chiều cao là \(h\) và bán kính đáy bằng \(r\), khi đó:
- Diện tích xung quanh của hình trụ:
\(\boxed{{S_{xq}} = 2\pi rh}\)
- Diện tích toàn phần của hình trụ:
\(\boxed{{S_{tp}} = {S_{xq}} + 2.{S_{đ}} = 2\pi rh + 2\pi {r^2}}\)
- Thể tích khối trụ:
\(\boxed{V = B.h = \pi {r^2}h}\)
Ví dụ:
Tính diện tích xung quanh, diện tích toàn phần của hình trụ biết hình trụ có bán kính đáy \(a\) và đường cao là \(a\sqrt 3\).
Giải:
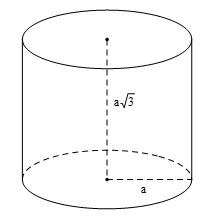
+) Theo đề bài, hình trụ có bán kính đáy \(a\) và đường cao \(a\sqrt 3\) nên
Diện tích xung quanh hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi a.a\sqrt 3 = 2\pi {a^2}\sqrt 3\)
Diện tích đáy của hình trụ là: \({S_{đ}} = \pi {a^2}\)
+) Áp dụng CT, ta có diện tích toàn phần của hình trụ là: \({S_{tp}} = 2\pi {a^2}\sqrt 3 + 2\pi {a^2} = 2\pi {a^2}(1 + \sqrt 3 )\)
4. Tính chất
- Nếu cắt mặt trụ tròn xoay (có bán kính là \(r\) ) bởi một \(mp\left( \alpha \right)\) vuông góc với trục \(\Delta\) thì ta được đường tròn có tâm trên \(\Delta\) và có bán kính bằng \(r\) với \(r\) cũng chính là bán kính của mặt trụ đó.
- Nếu cắt mặt trụ tròn xoay (có bán kính là \(r\)) bởi một \(mp\left( \alpha \right)\) không vuông góc với trục \(\Delta\) nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng \(2r\) và trục lớn bằng \(\frac{{2r}}{{\sin \varphi }}\), trong đó \(\varphi\) là góc giữa trục \(\Delta\) và \(mp\left( \alpha \right)\) với \({0^0} < \varphi < {90^0}\).
Chú ý:
Cho \(mp\left( \alpha \right)\) song song với trục \(\Delta\) của mặt trụ tròn xoay và cách \(\Delta\) một khoảng d.
- Nếu \(d < r\) thì \(mp\left( \alpha \right)\) cắt mặt trụ theo hai đường sinh \(\Rightarrow\) Thiết diện là hình chữ nhật.
- Nếu \(d = r\) thì \(mp\left( \alpha \right)\) tiếp xúc với mặt trụ theo một đường sinh.
- Nếu \(d > r\) thì \(mp\left( \alpha \right)\) không cắt mặt trụ.
Ví dụ:
Tính thể tích của khối trụ biết bán kính đáy của hình trụ đó bằng \(a\) và thiết diện đi qua trục là một hình vuông.
Giải:
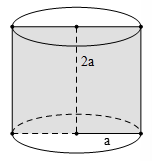
Theo bài ra thiết diện qua trục của hình trụ là hình vuông nên hình trụ có bán kính đáy là \(a\), chiều cao \(2a\). Do đó thể tích khối trụ là:
\(V = \pi {R^2}h = \pi {a^2}.2a = 2\pi {a^3}\).
