Xác định công thức hàm số
Hàm số ![]() có đạo hàm liên tục trên tập số thực và
có đạo hàm liên tục trên tập số thực và ![]() ;
; ![]() . Hàm số
. Hàm số ![]() là:
là:
Ta có:
Theo bài ra ta có:
Vậy .
Mời các bạn học cùng thử sức với đề Đề thi học kì 2 môn Toán lớp 12 nha!
Xác định công thức hàm số
Hàm số ![]() có đạo hàm liên tục trên tập số thực và
có đạo hàm liên tục trên tập số thực và ![]() ;
; ![]() . Hàm số
. Hàm số ![]() là:
là:
Ta có:
Theo bài ra ta có:
Vậy .
Kết luận nào sau đây là đúng?
Cho hàm số ![]() có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn ![]() và đồ thị hàm số
và đồ thị hàm số ![]() (như hình vẽ). biết
(như hình vẽ). biết ![]() và
và ![]() . Kết luận nào sau đây là đúng?
. Kết luận nào sau đây là đúng?
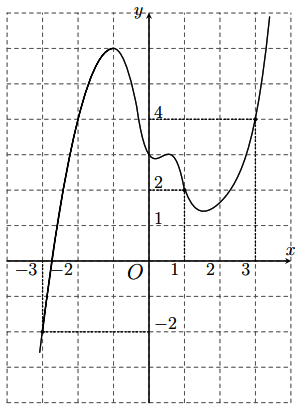
Hình vẽ minh họa:

Ta có:
Từ đồ thị ta thấy
Từ đồ thị ta thấy
=>
Mặt khác
Ta có bảng biến thiên như sau:

=> có duy nhất nghiệm trên
Tìm tọa độ M
Trong không gian ![]() , cho điểm
, cho điểm ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua
đi qua ![]() cắt các trục
cắt các trục ![]() ,
, ![]() lần lượt tại
lần lượt tại ![]() khác gốc tọa độ sao cho
khác gốc tọa độ sao cho ![]() đạt giá trị nhỏ nhất, trong đó
đạt giá trị nhỏ nhất, trong đó ![]() lần lượt là diện tích các tam giác
lần lượt là diện tích các tam giác ![]() và
và ![]() lần lượt là diện tích các tam giác
lần lượt là diện tích các tam giác ![]() . Điểm
. Điểm ![]() nào dưới đây thuộc
nào dưới đây thuộc ![]() ?
?
Ta có . Lại có
,
và
.
Đặt , ta có
Tương tự, ta có và
.
Khi đó .
Dấu "=" xảy ra khi và chỉ khi hay
.
Từ đó suy ra nhận
làm vectơ pháp tuyến.
Do đó có phương trình
.
Vậy là điểm thuộc
.
Tính giá trị biểu thức
Biết tích phân ![]()
![]() . Khi đó tích
. Khi đó tích ![]() có giá trị bằng
có giá trị bằng
Ta có:
Đặt
.
Điểm biểu diễn của số phức
Kí hiệu ![]() là nghiệm phức có phần ảo dương của phương trình
là nghiệm phức có phần ảo dương của phương trình ![]() . Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức
. Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức ![]() ?
?
Ta có:
Tính P
Kí hiệu ![]() là hai nghiệm phức của phương trình
là hai nghiệm phức của phương trình ![]() . Tính
. Tính ![]()
Phương trình có hai nghiệm
.
Khi đó
Chọn đáp án đúng
Công thức tính diện tích S của hình thang cong giới hạn bởi hai đồ thị ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Đáp án đúng: .
Số phức đối của số phức z
Cho số phức ![]() . Số phức đối của z có điểm biểu diễn là:
. Số phức đối của z có điểm biểu diễn là:
Tìm nguyên hàm của hàm số
Cho ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() . Tìm nguyên hàm của hàm số
. Tìm nguyên hàm của hàm số ![]() ?
?
Cách 1: Sử dụng tính chất của nguyên hàm
.
Từ giả thiết, ta có:
Suy ra .
Vậy
Cách 2: Sử dụng công thức nguyên hàm từng phần.
Nếu u, v là hai hàm số có đạo hàm liên tục trên K thì:
.
Ta có
Từ giả thiết: .
Vậy .
Chọn đáp án đúng
Trong không gian với hệ tọa độ ![]() phương trình đường thẳng
phương trình đường thẳng ![]() đi qua điểm A(2;-1; 3) và vuông góc với mặt phẳng
đi qua điểm A(2;-1; 3) và vuông góc với mặt phẳng ![]() là.
là.
có vectơ pháp tuyến
Vì vuông góc với
nên
có vectơ chỉ phương
đi qua điểm A và có vectơ chỉ phương
Vậy phương trình tham số của là
Tính giá trị của biểu thức
Biết hàm số ![]() có nguyên hàm là
có nguyên hàm là ![]() với
với ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() .
.
Ta có:
Mà
Số phức 5 + 6i có phần thực bằng
Số phức ![]() có phần thực bằng
có phần thực bằng
Số phức z = a + bi có b được gọi là phần thực.
Xác định vectơ pháp tuyến của mặt phẳng
Trong không gian với hệ trục tọa độ ![]() , cho mặt phẳng
, cho mặt phẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() có một vectơ pháp tuyến là
có một vectơ pháp tuyến là
Mặt phẳng có một vectơ pháp tuyến là
.
Chọn khẳng định đúng
Cho số phức ![]() thoả điều kiện
thoả điều kiện ![]() .
.
Đặt ![]() . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
Ta có:
Nhận xét: câu này đáp án A cũng đúng vì
Tìm họ nguyên hàm của hàm số
Họ nguyên hàm của hàm số ![]() là:
là:
Ta có: .
Tìm phần ảo của số phức
Cho hai số phức ![]() và
và ![]() . Tìm phần ảo b của số phức
. Tìm phần ảo b của số phức ![]() .
.
Ta có:
Tính giá trị biểu thức
Biết rằng ![]() liên tục trên
liên tục trên ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() . Giá trị biểu thức
. Giá trị biểu thức ![]() bằng:
bằng:
Ta có:
Vì hàm số liên tục trên
nên liên tục tại
tức là
Do đó
Tìm tọa độ điểm M
Trong không gian ![]() , điểm
, điểm ![]() thuộc trục
thuộc trục ![]() và cách đều hai mặt phẳng
và cách đều hai mặt phẳng ![]() và
và ![]() có tọa độ là?
có tọa độ là?
Ta có suy ra
.
Theo đề bài ra ta có:
Vậy .
Tìm tổng các giá trị
Tìm tổng các giá trị của số thực a sao cho phương trình ![]() có nghiệm phức
có nghiệm phức ![]() thỏa mãn
thỏa mãn ![]() .
.
4 || Bốn || bốn
Tìm tổng các giá trị của số thực a sao cho phương trình ![]() có nghiệm phức
có nghiệm phức ![]() thỏa mãn
thỏa mãn ![]() .
.
4 || Bốn || bốn
Ta có với mọi thì phương trình
luôn có nghiệm phức.
và
.
Suy ra .
Từ (1) ta có , từ (2) ta có
.
Vậy tổng .
Ghi đáp án vào ô trống
Trong không gian với hệ trục tọa độ ![]() , cho hình hộp chữ nhật
, cho hình hộp chữ nhật ![]() có điểm
có điểm ![]() trùng với gốc tọa độ
trùng với gốc tọa độ ![]() ,
, ![]()
![]() . Gọi
. Gọi ![]() là trung điểm của cạnh
là trung điểm của cạnh ![]() . Giá trị của tỉ số
. Giá trị của tỉ số ![]() để hai mặt phẳng
để hai mặt phẳng ![]() và
và ![]() vuông góc với nhau bằng bao nhiêu?
vuông góc với nhau bằng bao nhiêu?
Trong không gian với hệ trục tọa độ ![]() , cho hình hộp chữ nhật
, cho hình hộp chữ nhật ![]() có điểm
có điểm ![]() trùng với gốc tọa độ
trùng với gốc tọa độ ![]() ,
, ![]()
![]() . Gọi
. Gọi ![]() là trung điểm của cạnh
là trung điểm của cạnh ![]() . Giá trị của tỉ số
. Giá trị của tỉ số ![]() để hai mặt phẳng
để hai mặt phẳng ![]() và
và ![]() vuông góc với nhau bằng bao nhiêu?
vuông góc với nhau bằng bao nhiêu?
Tìm nghiệm?
Trong ![]() , phương trình
, phương trình ![]() có nghiệm là:
có nghiệm là:
Ta có: nên phương trình có hai nghiệm phức là:
Tìm phần thực và phần ảo của số phức
Cho hai số phức ![]() . Phần thực và phần ảo của số phức
. Phần thực và phần ảo của số phức ![]() tương ứng bằng:
tương ứng bằng:
Ta có:
V khối lập phương
Tính thể tích ![]() của khối lập phương
của khối lập phương ![]() , biết
, biết ![]() .
.

Đặt cạnh của khối lập phương là
Suy ra .
Tam giác vuông , có
Vậy thể tích khối lập phương .
Phần thực và phần ảo của số phức
Cho số phức z thỏa mãn ![]() . Khi đó phần thực và phần ảo của z là
. Khi đó phần thực và phần ảo của z là
Ta có:
Chọn phương án thích hợp
Tích phân  có giá trị là:
có giá trị là:
Tích phân có gái trị là:
Ta có:
Suy ra .
Đặt .
Đổi cận
Xét .
Đặt .
Đổi cận .
.
Xét .
Đặt .
Đổi cận .
.
.
Đáp án đúng là
Chọn khẳng định đúng
Trong các khẳng định sau khẳng định nào đúng.
Ta có:
Khi đó:
Tính thể tích V
Cho ![]() là hình phẳng giới hạn bởi đường cong
là hình phẳng giới hạn bởi đường cong ![]() và đường thẳng
và đường thẳng ![]() . Tính thể tích
. Tính thể tích ![]() của vật thể tròn xoay do hình phẳng
của vật thể tròn xoay do hình phẳng ![]() quay quanh trục hoành.
quay quanh trục hoành.
Phương trình hoành độ giao điểm là:
Thể tích cần tính là:
Tìm đáp án đúng
Tìm nguyên hàm ![]() của hàm số
của hàm số ![]() với
với ![]() .
.
Ta có
Xác định vectơ pháp tuyến của mặt phẳng
Trong không gian ![]() , mặt phẳng
, mặt phẳng ![]() có một vectơ pháp tuyến là:
có một vectơ pháp tuyến là:
Mặt phẳng có một vectơ pháp tuyến là:
.
Tìm tọa độ
Cho M trên đường thẳng AB với ![]() và
và ![]() . Nếu
. Nếu ![]() với
với ![]() thì tọa độ của M là:
thì tọa độ của M là:
Vì M nằm trên AB và nên khi xét theo tọa độ vecto 2 điểm A và B, ta có:
Tính tổng?
Cho số phức ![]() thỏa mãn
thỏa mãn ![]() . Viết
. Viết ![]() dưới dạng
dưới dạng ![]() . Khi đó tổng
. Khi đó tổng ![]() có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
10
Cho số phức ![]() thỏa mãn
thỏa mãn ![]() . Viết
. Viết ![]() dưới dạng
dưới dạng ![]() . Khi đó tổng
. Khi đó tổng ![]() có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
10
Ta có:
Suy ra .
Tính giá trị biểu thức M
Cho biểu thức ![]() với
với ![]() . Biểu thức M có giá tri là?
. Biểu thức M có giá tri là?
Ta có: .
Khi đó:
.
Tìm số phức thỏa mãn điều kiện
Số phức có phần thực bằng 1 và phần ảo bằng 3 là
Số phức z = a + bi có a được gọi là phần ảo, b là phần thực.
Tìm phần thực?
Số phức ![]() có phần thực là?
có phần thực là?
2
Số phức ![]() có phần thực là?
có phần thực là?
2
Ta có:
Vậy phần thực của số phức
Tính giá trị
Cho phương trình ![]() có hai nghiệm
có hai nghiệm ![]() là . Giá trị của
là . Giá trị của ![]() là?
là?
1 || Một || một
Cho phương trình ![]() có hai nghiệm
có hai nghiệm ![]() là . Giá trị của
là . Giá trị của ![]() là?
là?
1 || Một || một
Ta có:
Suy ra:
Xét tính đúng sai của các khẳng định
Trong không gian với hệ tọa độ ![]() , cho hai đường thẳng:
, cho hai đường thẳng:![]() và
và ![]()
a) Vectơ có tọa độ ![]() là một vectơ chỉ phương của
là một vectơ chỉ phương của ![]() . Sai||Đúng
. Sai||Đúng
b) Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() . Đúng||Sai
. Đúng||Sai
c) Đường thẳng ![]() đi qua
đi qua ![]() và vuông góc với
và vuông góc với ![]() có phương trình tham số là
có phương trình tham số là  . Đúng||Sai
. Đúng||Sai
d) Góc giữa hai đường thẳng ![]() và
và ![]() khoảng
khoảng ![]() . Sai||Đúng
. Sai||Đúng
Trong không gian với hệ tọa độ ![]() , cho hai đường thẳng:
, cho hai đường thẳng:![]() và
và ![]()
a) Vectơ có tọa độ ![]() là một vectơ chỉ phương của
là một vectơ chỉ phương của ![]() . Sai||Đúng
. Sai||Đúng
b) Đường thẳng ![]() đi qua điểm
đi qua điểm ![]() . Đúng||Sai
. Đúng||Sai
c) Đường thẳng ![]() đi qua
đi qua ![]() và vuông góc với
và vuông góc với ![]() có phương trình tham số là
có phương trình tham số là  . Đúng||Sai
. Đúng||Sai
d) Góc giữa hai đường thẳng ![]() và
và ![]() khoảng
khoảng ![]() . Sai||Đúng
. Sai||Đúng
a) Vectơ có tọa độ là một vectơ chỉ phương của
nên mệnh đề sai
b) Mệnh đề đúng
c) Gọi
nên mệnh đề đúng
d) Góc giữa hai đường thẳng luôn là góc nhọn nên mệnh đề sai
Tìm tọa độ vectơ
Trong không gian với hệ trục tọa độ ![]() , cho
, cho ![]() ,
, ![]() ,
, ![]() . Tìm tọa độ của vectơ
. Tìm tọa độ của vectơ ![]() .
.
Ta có:
.
Xác định tọa độ vectơ
Trong không gian ![]() , véctơ
, véctơ ![]() vuông góc với hai véctơ
vuông góc với hai véctơ ![]() và
và ![]() ; đồng thời
; đồng thời ![]() tạo với tia
tạo với tia ![]() một góc tù và độ dài véctơ
một góc tù và độ dài véctơ ![]() bằng 3. Tìm véctơ
bằng 3. Tìm véctơ ![]() .
.
Ta có và
không cùng phương đồng thời
.
Do .
Mặt khác tạo với tia
một góc tù nên
.
Suy ra .
Vậy .
Tính giá trị biểu thức
Gọi ![]() là một nguyên hàm của hàm số
là một nguyên hàm của hàm số ![]() , thỏa mãn
, thỏa mãn ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() ?
?
Ta có:
là một nguyên hàm của hàm số
, ta có:
mà
Tính giá trị
Biết ![]() và
và ![]() là hai nghiệm phức của phương trình:
là hai nghiệm phức của phương trình: ![]() . Khi đó
. Khi đó ![]() bằng:
bằng:
Ta có:
Áp dụng hệ thức Viet ta có:
Suy ra ta có:.
Tìm câu sai
Cho hàm số ![]() . Gọi
. Gọi ![]() là một nguyên hàm của
là một nguyên hàm của ![]() . Chọn phương án sai.
. Chọn phương án sai.
Ta có
Từ đây ta thấy đúng.
Với ta thấy
, vậy
sai.
Tìm câu sai
Các mệnh đề sau, mệnh đề nào sai.
Đáp án sai:
Mô đun số phức
Cho số phức z thỏa mãn ![]() . Môđun của z là:
. Môđun của z là:
Giả sử: .
Chọn đáp án đúng
Với phương pháp đổi biến số ![]() , nguyên hàm
, nguyên hàm ![]() bằng:
bằng:
Ta biến đổi: .
Đặt .
.
Tính giá trị x và y thỏa mãn điều kiện
Cho ![]() . Giá trị của x và y bằng:
. Giá trị của x và y bằng:
Ta có:
Ghi đáp án đúng vào ô trống
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị trên mỗi trục tính theo kilômét. Máy bay điều khiển xuất phát phải đi qua điểm ![]() và bay với vận tốc không đổi về vạch đích trong không trung được xác định bởi 1 đường màu từ hai drone (máy bay không người lái) cố định toạ độ là
và bay với vận tốc không đổi về vạch đích trong không trung được xác định bởi 1 đường màu từ hai drone (máy bay không người lái) cố định toạ độ là ![]() . Máy bay sẽ bay qua điểm
. Máy bay sẽ bay qua điểm ![]() của đường màu
của đường màu ![]() để thời gian về đích là nhanh nhất. Giả sử toạ độ điểm
để thời gian về đích là nhanh nhất. Giả sử toạ độ điểm ![]() , hãy tính giá trị biểu thức
, hãy tính giá trị biểu thức ![]() .
.
Đáp án: 50
Trong không gian chọn hệ trục tọa độ cho trước, đơn vị trên mỗi trục tính theo kilômét. Máy bay điều khiển xuất phát phải đi qua điểm ![]() và bay với vận tốc không đổi về vạch đích trong không trung được xác định bởi 1 đường màu từ hai drone (máy bay không người lái) cố định toạ độ là
và bay với vận tốc không đổi về vạch đích trong không trung được xác định bởi 1 đường màu từ hai drone (máy bay không người lái) cố định toạ độ là ![]() . Máy bay sẽ bay qua điểm
. Máy bay sẽ bay qua điểm ![]() của đường màu
của đường màu ![]() để thời gian về đích là nhanh nhất. Giả sử toạ độ điểm
để thời gian về đích là nhanh nhất. Giả sử toạ độ điểm ![]() , hãy tính giá trị biểu thức
, hãy tính giá trị biểu thức ![]() .
.
Đáp án: 50
Ta có:
Đường thẳng (BC) đi qua điểm B có VTCP có dạng
Điểm và
Ta có:
Vậy
Tìm phần thực và phần ảo
Cho số phức z thỏa mãn ![]() . Khi đó phần thực và phần ảo của z lần lượt là?
. Khi đó phần thực và phần ảo của z lần lượt là?
Ta có:
Vậy số phức z có phần thực bằng 0 và phần ảo bằng 1.
Tính giá trị của biểu thức
Biết hàm số ![]() có nguyên hàm là
có nguyên hàm là ![]() với
với ![]() . Tính giá trị biểu thức
. Tính giá trị biểu thức ![]() .
.
Ta có:
Mà
Viết phương trình đường thẳng
Cho các số phức z thỏa mãn ![]() . Tập hợp các điểm biểu diễn các số phức
. Tập hợp các điểm biểu diễn các số phức ![]() trên các mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó.
trên các mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó.
Đặt
Khi đó phương trình
Với
Xác định số phức z
Cho hai số phức ![]() và
và ![]() . Tìm số phức
. Tìm số phức ![]()
Ta có:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
